RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Miscellaneous Exercise is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Miscellaneous Exercise.
| Board | RBSE |
| Te×tbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Polynomials |
| E×ercise | Miscellaneous Exercise |
| Number of Questions Solved | 23 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Miscellaneous Exercise
Multiple Choice Questions
RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 1.
If one zero of polynomial f(x) = 5x2 + 13x + k is inverse of (RBSESolutions.com) other, then k will be :
(A) 0
(B) \(\frac { 1 }{ 5 }\)
(C) 5
(D) 6
Solution

RBSE Class 10 Maths Chapter 3 Miscellaneous Question 2.
Zeros of (RBSESolutions.com) polynomial x2 – x – 6 are :
(A) 1, 6
(B) 2, -3
(C) 3, -2
(D) 1, -6
Solution
f(x) = x2 – x – 6
= x2 – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x – 3)(x + 2)
for zeros f(x) = 0
⇒ (x – 3)(x + 2) = 0
⇒ x = 3 or x = -2
Hence, option (C) is correct.
RBSE Solutions For Class 10 Maths Chapter 3 Question 3.
If 3 is a zero of polynomial 2x2 + x + k, then (RBSESolutions.com) value of k will be
(A) 12
(B) 21
(C) 24
(D) -21
Solution
Let f(x) = 2x2 + x + k
One zero is 3
f(3) = 0
⇒ 2(3)2 + 3 + k = 0
⇒ 2 × 9 + 3 + k = 0
⇒ 18 + 3 + k = 0
⇒ k = -21
Hence, option (D) is correct.
Miscellaneous Exercise 3 Class 10 Question 4.
If α, β are zeros of (RBSESolutions.com) polynomial x2 – p(x + 1) – c such that (α + 1)(β + 1) = 0, then c will
(A) 0
(B) -1
(C) 1
(D) 2
Solution

RBSE Solution Class 10 Maths Chapter 3 Question 5.
If roots of quadratic (RBSESolutions.com) equation x2 – kx + 4 = 0 then k will be
(A) 2
(B) 1
(C) 4
(D) 3
Solution
Given equation x2 – kx + 4 = 0
Comparing it with ax2 + bx + c = 0
We get a = 1, b= -k and c = 4
D = b2 – 4 ac = (-k)2 – 4 × 1 × 4 = k2 – 16
Roots are same
D = 0
⇒ k2 – 16 = 0
⇒ k2 = 16
⇒ k = ±√16
⇒ k = ± 4
Hence, option (C) is correct.
Class 10 Maths RBSE Solution Chapter 3 Question 6.
If x = 1, is common root of (RBSESolutions.com) equation ax2 + ax + 3 = 0 and x2 + x + b = 0, then ab will be:
(A) 1
(B) 3.5
(C) 6
(D) 3
Solution
Putting x = 1 in equation
ax2 + ax + 3 = 0
⇒ a(1)2 + a(1) + 3 = 0
⇒ a + a + 3 = 0
⇒ 2a = – 3
⇒ a = \(\frac { -3 }{ 2 }\)
and putting x = 1 in equation
x2 + x + b = 0
⇒ (1)2 + (1) + b = 0
⇒ 1 + 1 + b = 0
⇒ b = -2
ab = \(\frac { -3 }{ 2 }\) × -2 = 3
Hence, option (D) is correct.
Class 10 RBSE Maths Solution Ch 3 Question 7.
Discriminant of quadratic (RBSESolutions.com) equation 3√3 x2 + 10x + √3 = 0
(A) 10
(B) 64
(C) 46
(D) 30
Solution
Comparing 3√3x2 + 10x + √3 by ax2 + bx + c = 0,
a = √3, b = 10 and c = √3
Discriminant(D) = b2 – 4ac
= (10)2 – 4 × 3√3 × √3
= 100 – 4 × 3 × 3
= 100 – 36
= 64
Hence, option (B) is correct.
RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 8.
Nature of roots of quadratic (RBSESolutions.com) equation 4x2 – 12x – 9 = 0 is :
(A) Real and same
(B) Real and distinct
(C) Imgiary and same
(D) Imaginary and distinct
Solution
Given equations 4x2 – 12x – 9 = 0
Where a = 4, b = -12, c = -9
Discriminant (D) = b2 – 4ac
= (-12)2 – 4 × 4 × (-9)
= 144 + 144
= 288 > 0
Hence, option (B) is correct.
RBSE Solutions For Class 10 Maths Chapter 3 Question 9.
H.C.F. of (RBSESolutions.com) expressions 8a2b2c and 20ab3c2 is:
(A) 4ab2c
(B) 4abc
(C) 40a2b3c2
(D) 40abc
Solution
8a2b2c = 2 × 2 × 2 × a2 × b2 × c = 23 × a2 × b2 × c
and 20ab3c3 = 2 × 2 × 5 × a × b3 × c3 = 22 × 5 × a × b3 × c3
Product of common least power = 22 × a × b2 × c = 4ab2c
Hence, option (A) is correct.
RBSE Class 10 Maths Chapter 3 Miscellaneous Question 10.
Find L.C. M. of expressions x2 – 1 and x2 + 2x + 1
(A) x + 1
(B) (x2 – 1) (x – 1)
(C) (x – 1) (x + 1)2
(D) (x2 – 1) (x + 1)
Solution
x2 – 1 = (x – 1) (x + 1)
and x2 + 2x + 1 = (x + 1) (x + 1) = (x + 1)2
Product of highest powers = (x – 1)(x + 1)2
Hence, option (C) is correct.
RBSE Class 10 Maths Chapter 3 Miscellaneous Question 11.
L.C.M. of (RBSESolutions.com) expressions 6x2y4 and 10xy2, then 30x2y4 H.C.F. will be:
(A) 6x2y2
(B) 2xy2
(C) 10x2y2
(D) 60x3y6
Solution :

RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 12.
To find roots of quadratic (RBSESolutions.com) equation ax2 + bx + c = 0 write Shridhar Acharya formula.
Solution
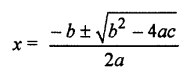
RBSE Class 10 Maths Chapter 3 Miscellaneous Exercise Question 13.
Write nature of roots by general form of discriminant of equation ax2 + bx + c = 0.
Solution
Nature of roots of quadratic equation ax2 + bx + c = 0, a 0 depends on its discriminant value, D = b2 – 4ac
(i) If D = b2 – 4ac > 0, then roots will be real and distinct.
If α and β are roots of the equation then
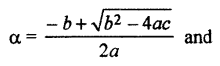
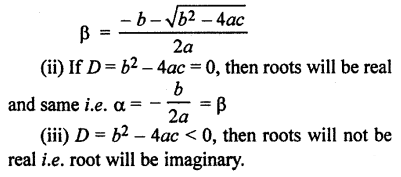
Miscellaneous Exercise Class 10 Question 14.
Find zeros of quadratic (RBSESolutions.com) equation 2x2 – 8x + 6 and test the relationship between zeros and coefficient.
Solution
Given polynamial
f(x) = 2x2 – 8x + 6
= 2x2 – 6x – 2x + 6
= 2x(x – 3) – 2(x – 3)
= (x – 3) (2x – 2)
To find zeros of polynomial f(x), f(x) = 0.
⇒ f(x) = 0
⇒ (x – 3)(2x – 2) = 0
⇒ x – 3 = 0 or 2x – 2 = 0
⇒ x – 3 or x = 1
Zeros of polynomial 2x2 – 8x + 6 are 1 and 3.
Relation between zeros and coefficient:
Sum of zeros = 1 + 3 = 4
Product of zeros = 1 × 3 = 3
comparing (RBSESolutions.com) polynomial by ax2 + bx + c = 0
a = 2, b = -8, c = 6
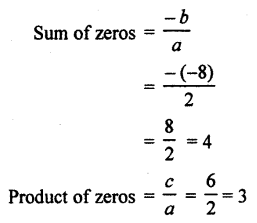
Thus there is a relationship between zeros and coefficient.
RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 15.
If α and β are zeros of quadratic (RBSESolutions.com) equation f(x) = x2 – px + q, then find the values of the following:
(a) α2 + β2
(b) \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\)
Solution
Given α and β are zeros quadratic equation f(x) = x2 – px + q
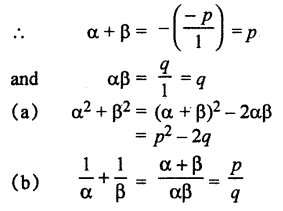
RBSE Maths Solution Class 10 Chapter 3 Question 16.
If polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided (RBSESolutions.com) by another polynamial x2 – 2x + k and remainder obtained x + a, then find k and a.
Solution
Given x4 – 6x3 + 16x2 – 25x + 10 divided by x2 – 2x + k obtained remainder is x + a


RBSE Solutions For Class 10 Maths Chapter 12 Miscellaneous Question 17.
The area of a rectangular (RBSESolutions.com) plot is 528 m2. Length of a plot (in m) is 1 more than twice of breadth. By forming quadratic equation, find the length and breadth of the plot.
Solution
Let breadth of a plot is x m.
According to question,
Length of plot = (2 × breadth) + l = (2 × x + 1) = (2x + 1) m.
Area of rectangular plot = l × b = (2x + 1) × x = (2x2 + x) sq. m.
Given : Area of plot = 528 sq. m.
2x2 + x = 528
⇒ 2x2 + x – 528 = 0
Required quadratic (RBSESolutions.com) equation is :
2x2 + x – 528 = 0
⇒ 2x2 + 33x – 32x – 528 = 0
⇒ x(2x + 33) – 16(2x + 33) = 0
⇒ (2x + 33) (x – 16) = 0
⇒ x – 16 = 0 or 2x + 33 = 0
⇒ x = 16 or x = \(\frac { –33 }{ 2 }\) (impossible)
Hence, Length of plot is 2x + 1 = 2 × 16 + 1 = 33 m
and breadth is 16 m.
Exercise 3.5 Class 10 RBSE Question 18.
Solve quadratic (RBSESolutions.com) equation x2 + 4x – 5 = 0 by completing the square method.
Solution
Given quadratic equation
x2 + 4x – 5 = 0
⇒ x2 + 4x = 5
Adding square of half of coefficient of x on both sides
x2 + 2 × 2x + (2)2 = 5 + (2)2
⇒ (x + 2)2 = 5 + 4
⇒ (x + 2)2 = 9
⇒ x + 2 = ±√9
⇒ x + 2 = ± 3
Taking + ve sign x = 3 – 2 = 1
Taking – ve sign x = -3 – 2 = – 5
Hence, solution of given quadratic equation are 1 and – 5.
RBSE Solutions For Class 10 Maths Chapter 3 Miscellaneous Question 19.
Solve the following (RBSESolutions.com) equations by factorisation method.
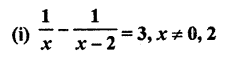
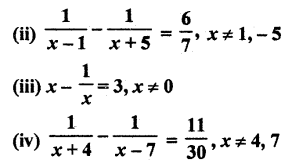
Solution

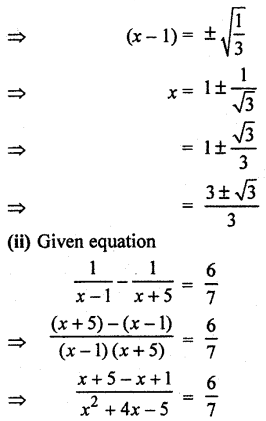

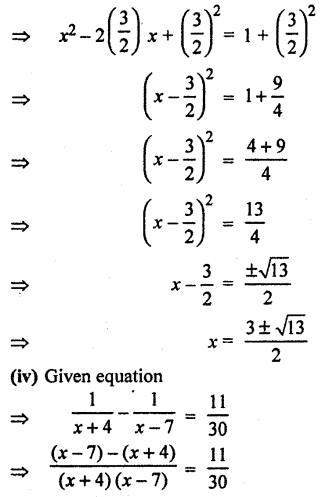

RBSE Class 10 Maths Chapter 4 Miscellaneous Solutions Question 20.
If -5 is a root of quadratic (RBSESolutions.com) equation 2x2 + px – 15 = 0 and roots of quadratic equation p(x2 + x) + k = 0 are same, then find k.
Solution
Given
One root of quadratic equation 2x2 + px – 15 = 0 is -5.
2(-5)2 + p(-5) – 15 = 0
⇒ 2 × 25 – 5p – 15 = 0
⇒ 50 – 5p – 15 = 0
⇒ 5p = 35
⇒ p = 7
Putting this value in (RBSESolutions.com) quadratic equation p(x2 + x) + k = 0
7 (x2 + x) + k = 0
⇒ 7x2 + 7x + k = 0
Comparing by ax2 + bx + c = 0
a = 7, b = 7 c = k
root of equation are equal
Discriminant (D) = 0
⇒ b2 – 4ac = (7)2 – 4 × 7 × k
⇒ 0 = 49 – 28k
⇒ 28k = 49
⇒ k = \(\frac { 49 }{ 28 }\)
Thus, k = \(\frac { 7 }{ 4 }\)
Chapter 3 Maths Class 10 Question 21.
Using, Shridhar Acharya (RBSESolutions.com) formula, solve the following quadratic equations : p2x2 + (p2 – q2) x – q2 = 0
Solution
Given equation p2x2 + (p2 – q2) x – q2 = 0
Comparing by ax2 + bx + c = 0, we get
a = p2, b = (p2 – q2) and c = -q2
By Shridhar Acharya formula
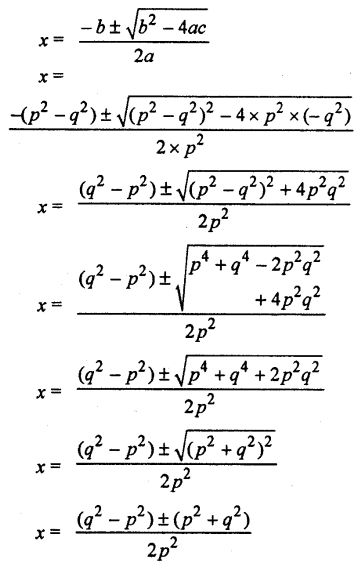

Class 10 Maths Chapter 3 Question 22.
L.C.M. and H.C.F. of two quadratic (RBSESolutions.com) expression are respectively x3 – 7x + 6 and (x – 1). Find the expression.
Solution
Least common multipile (L.C.M.) = x3 – 7x + 6
Highest common factor (H.C.F.) = (x – 1)
Factorising expression x3 – 7x + 6
putting x = 1 in this expression, we get = (1)3 – 7(1) + 6 = 1 – 7 + 6 = 0
At x = 0, expression = 0
(x – 1) is a factor
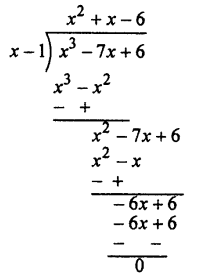
(x3 – 7x + 6)
= (x – 1) (x2 + x – 6)
= (x – 1) [x2 + 3x – 2x – 6]
= (x – 1)[x(x + 3) – 2(x + 3)]
= (x – 1)(x + 3)(x – 2)
Now L.C.M. = (x – 1) (x – 2) (x + 3)
and H.C.F. = (x – 1)
factror (x – 1) will be (RBSESolutions.com) common in two expressions
first expression = (x – 1) (x – 2) = x2 – 3x + 2
and second expression = (x – 1)(x + 3) = x2 + 2x – 3
Miscellaneous Exercise 3 Class 10 Question 23.
L.C.M. of two polynomials is x3 – 6x2 + 3x + 10 and H.C.F. is (x + 1) if one polynomial is x2 – 4x – 5, then find the other.
Solution
L.C.M. = x3 – 6x2 + 3x + 10
H.C.F. = (x + 1)
Putting x = 1 in x3 – 6x2 + 3x + 10
x = 1 putting
= (1)3 – 6(1)2 + 3(1) + 10
= 1 – 6 + 3 + 10 ≠ 0
putting x = -1
= (-1)3 – 6(-1)2 + 3(-1) + 10
= -1 – 6 – 3 + 10 = 0
at x = – 1, expression = 0
(x + 1) is a factor of expression
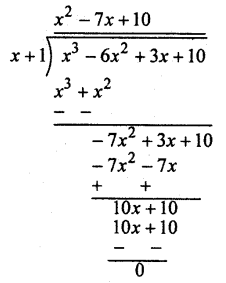

We hope the given RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Miscellaneous Exercise will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Miscellaneous Exercise, drop a comment below and we will get back to you at the earliest.