RBSE Solutions for Class 10 Maths Chapter 1 Vedic Mathematics Ex 1.4 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 1 Vedic Mathematics Exercise 1.4.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Vedic Mathematics |
| Exercise | Exercise 1.4 |
| Number of Questions Solved | 20 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 1 Vedic Mathematics Ex 1.4
Using the Sutra Paravartya Yogurt, Solve orally the following questions
Question 1.
13x – 14 = 9x + 10
Solution
We know (RBSESolutions.com) that
Algebraic formula ax + b = cx + d then
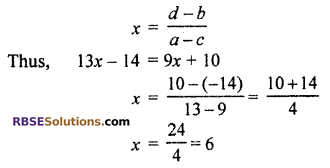
Question 2.
3y + 4 = 5y – 4
Solution
We know that
Algebraic formula ax + b = cx + d then
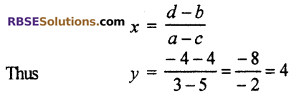
![]()
Question 3.
\(\frac { 2x+1 }{ 3x+4 }\) = \(\frac { 1 }{ 3 }\)
Solution
We know (RBSESolutions.com) that
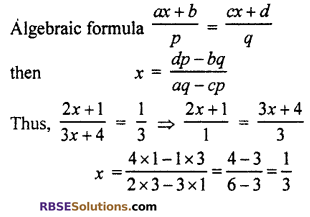
Question 4.
\(\frac { 5x-3 }{ 2 }\) = \(\frac { 2x+1 }{ 5 }\)
Solution
We know that
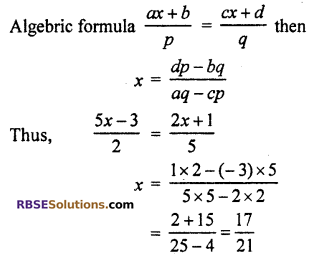
Question 5.
(x + 7)(x + 9) = (x – 8)(x – 11)
Solution
We know that (RBSESolutions.com) if equation
(x + a)(x + b) = (x + c)(x + d)
then putting values a = 7, b = 9, c = -8 and d = – 11
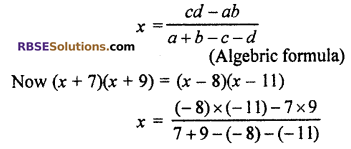
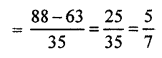
Question 6.
(x + 5)(x + 1) = (x + 3)(x + 2)
Solution
We know that, (RBSESolutions.com) if equation
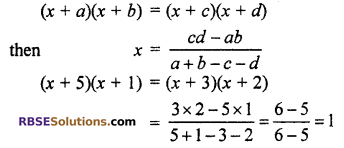
Question 7.
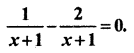
Solution
We know that if

![]()
Question 8.
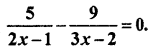
Solution

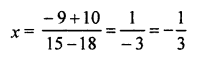
Using the sutra Shunyam Samyaschahye, Solve the equation:
Question 9.
(2x + 1) + (x + 3) = 5x + 4
Solution
(2x + 1) + (x + 3) = 5x + 4 independent (RBSESolutions.com) term of both sides are same (= 4)
So, x = 0.
Question 10.
a(x – 1) + b(x – 1) = c(x – 1) + d(x – 1)
Solution
Here
a(x – 1) + b(x – 1) = c(x – 1) + d(x – 1)
Thus, (x – 1) is common factor is both sides, then
x – 1 = 0
⇒ x = 1
Question 11.
(x + 1)(x + 9) = (x + 3)(x + 3)
Solution
(x + 1)(x + 9) = (x + 3)(x + 3)
Here independent term in both sides are same (= 9) then x = 0
Question 12.
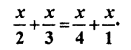
Solution
Numerator (x) is (RBSESolutions.com) same in both sides
Sum of denominators in R.H.S. = 2 + 3 = 5
Sum of denominators in R.H.S. = 4 + 1 = 5
Thus, According to formula, x = 0
Question 13.
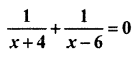
Solution
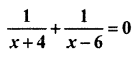
Here Numerator of two fractions are same = 1,
So According to formula :
x + 4 + x- 6 = 0
⇒ 2x – 2 = 0
⇒ 2x =
⇒ x = 1
![]()
Question 14.
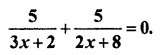
Solution
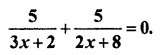
Here, Numerator of two (RBSESolutions.com) fractions are same = 5,
So according to formula :
3x + 2 + 2x + 8 = 0
⇒ 3x + 2x + 2 + 8 = 0
⇒ 5x + 10 = 0
⇒ 5x = -10
⇒ x = -2
Question 15.
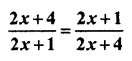
Solution
Sum of numerators of both sides = 2x + 4 + 2x + 1 = 4x + 5
Sum of denominators in both sides = 2x + 1 + 2x + 4 = 4x + 5
Two sums are equal, so by the formula
4x + 5 = 0
⇒ 4x = -5
⇒ x = \(\frac { -5 }{ 4 }\)
Question 16.
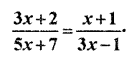
Solution
Sum of numerators (RBSESolutions.com) of two sides = 3x + 2 + x + 1 = 4x + 3 …..(i)
Sum of denominators of two sides = 5x + 7 + 3x – 1 = 8x + 6 …(ii)
Ratio of (i) and (ii) is 1 : 2.
So, by formula, equation any sum equal to zero,
4x + 3 = 0
⇒ 4x = – 3
⇒ x = \(\frac { -3 }{ 4 }\)
Question 17.
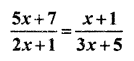
Solution
Difference between numerator and denominator = 5x + 7 – 2x – 1 = 3x + 6 = 3(x + 2) …(i)
Difference between numerator and denominator is R.H.S. = 3x + 5 – x – 1 = 2x + 4 = 2(x + 2) …(ii)
Ratio of (i) and (ii) is 3 : 2 THus, by formula
3(x + 2) = 0
⇒ x + 2 = 0
⇒ x = -2
Question 18.
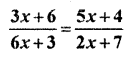
Solution
Difference between numerator (RBSESolutions.com) and denominator in L.H.S. = 6x + 3 – 3x – 6 = 3x – 3 …(i)
Difference numerator and denominator is L.H.S. = 5x + 4 – 2x – 7 = 3x – 3 …(ii)
Difference numerator and denominator in R.H.S.
3x – 3 = 0
⇒ 3x = 3
⇒ x = 1
Thus, x = 1
(i) and (ii) are equal, so by formula
3x + 6 + 5x + 4 = 8x + 10 …(i)
Adding denominators of both sides
6x + 3 + 2x + 7 = 8x + 10 …(ii)
(i) and (ii) are equal so by formula.
8x + 10 = 0
⇒ 8x = – 10
⇒ x = \(\frac { -10 }{ 8 }\) = \(\frac { -5 }{ 4 }\)
thus, x = \(\frac { -5 }{ 4 }\) and x = 1
![]()
Question 19.
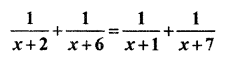
Solution
Sum of (RBSESolutions.com) denominators of L.H.S. = x + 2 + x + 6 = 2x + 8 …(i)
Sum of denominators of R.H.S. = x + 1 + x + 7 = 2x + 8 …(ii)
(i) and (ii) are equal so by formula
2x + 8 = 0
⇒ 2x = -8
⇒ x = -4
Question 20.
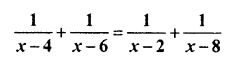
Solution
Sum of denominators ofL.H.S. = x – 4 + x – 6 = 2x – 10 …(i)
Sum of denominators of R.H.S. = x – 2 + x – 8 = 2x – 10 …(ii)
(i) and (ii) are same so by formula
2x – 10 = 0
⇒ 2x = 10
⇒ x = 5
We hope the given RBSE Solutions for Class 10 Maths Chapter 1 Vedic Mathematics Ex 1.4 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 1 Vedic Mathematics Exercise 1.4, drop a comment below and we will get back to you at the earliest.