RBSE Solutions for Class 10 Maths Chapter 1 वैदिक गणित Ex 1.4 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 1 वैदिक गणित Exercise 1.4.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | वैदिक गणित |
| Exercise | Exercise 1.4 |
| Number of Questions Solved | 20 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 1 वैदिक गणित Ex 1.4
सूत्रे परावर्त्य योजयेत् द्वारा समीकरण का मौखिक हल ज्ञात कीजिए।
![]()
प्रश्न 1.
13x – 14 = 9x + 10
हल:
a = 13, b = – 14, c = 9, d = 10
हम(RBSESolutions.com) जानते हैं।
यदि ax + b = cx + d तो
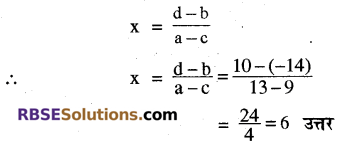
![]()
प्रश्न 2.
3y +4 = 5y – 4
हल:
a = 3, b = 4, c = 5, d = – 4
हम जानते हैं ।
यदि ax + b = cx.+ d तो
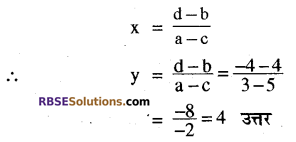
प्रश्न 3.
\(\frac { 2x+1 }{ 3x+4 } =\frac { 1 }{ 3 } \)
हल:

![]()
प्रश्न 4.
\(\frac { 5x-3 }{ 2 } =\frac { 2x+1 }{ 5 } \)
हल:
यहाँ a = 5, b = – 3, c = 2, d = 1, 2 = 2, q = 5
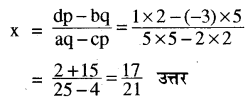
प्रश्न 5.
(x + 7) (x + 9) = (x – 8) (x – 11)
हल:
a = 7, b = 9, c = – 8, d = – 11
यदि (x + a) (x + b) = (x + c) (x + d) हो तो
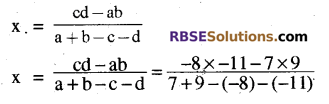
![]()
प्रश्न 6.
(x + 5) (x + 1) = (x + 3) (x + 2)
हल:
a = 5, b = 1, c = 3, d = 2
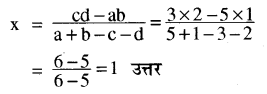
प्रश्न 7.
\(\frac { 1 }{ x-1 } -\frac { 2 }{ x+1 } =0\)
हल:
हम जानते हैं कि यदि

प्रश्न 8.
\(\frac { 5 }{ 2x-1 } -\frac { 9 }{ 3x-2 } =0\)
हल:
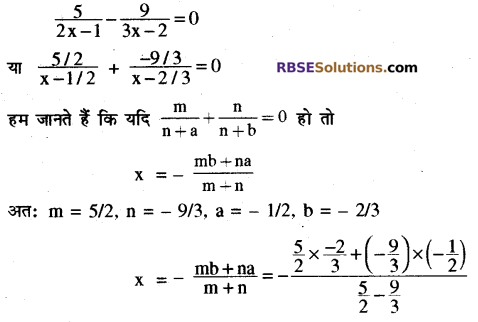
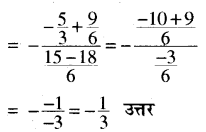
![]()
सूत्र शून्यं साम्य समुच्चये द्वारा समीकरण हल कीजिये।
प्रश्न 9.
(2x + 1) + (x + 3) = (5x + 4)
हल:
एक घातीय समीकरण के दोनों पक्षों में (RBSESolutions.com)स्वतंत्र पद समान हो तो चर राशि का मान शून्य होता है।
अतः यहाँ 1 + 3 = 4 दोनों पक्षों में स्वतंत्र पद समान है।
अतः x = () होगा।
![]()
प्रश्न 10.
a(x – 1) + b(x – 1) = c(x – 1) + d(x – 1)
हल:
यहाँ (x – 1) एक सर्वनिष्ठ खण्ड है।
अतः (x – 1) = () ∴ x = 1
प्रश्न 11.
(x + 1) (x + 9) = (x + 3) (x + 3)
हल:
यहाँ दोनों ओर स्वतंत्र पद 9 है जो समान है।
अतः x = 0 मान होगा।
प्रश्न 12
\(\frac { x }{ 2 } +\frac { x }{ 3 } =\frac { x }{ 4 } +\frac { x }{ 1 } \)
हल:
प्रत्येक पद में x एक उभयनिष्ठ खण्ड है।
अतः x = 0
प्रश्न 13.
\(\frac { 1 }{ x+4 } +\frac { 1 }{ x-6 } =0\)
हल:
सूत्र तृतीय के अनुसार
यदि समीकरणों में दो भिन्नों के अंश परस्पर (RBSESolutions.com)समान हों तो उनके हरों का योग शून्य रखने पर चर राशि का मान प्राप्त होता है।
यहाँ दोनों भिन्नों के अंश परस्पर समान = 1
अतः सूत्रानुसार हरों का योग = x + 4 + x – 6 = 0
अतः 2x – 2 = 0, x = 2/2 = 1
![]()
प्रश्न 14.
\(\frac { 5 }{ 3x+2 } +\frac { 5 }{ 2x+8 } =0\)
हल:
अंश के दोनों अंक परस्पर समान = 5 है। अतः हरों का योग = 3x + 2 + 2x + 8 = 0
या 5x + 10 = 0
अतः \(\quad x=\frac { -10 }{ 5 } =-2\) उत्तर
प्रश्न 15.
\(\frac { 2x+4 }{ 2x+1 } =\frac { 2x+1 }{ 2x+4 } \)
हल:
सूत्र चतुर्थ-यदि समीकरण के दोनों पक्षों के अंशों(RBSESolutions.com) का योग तथा उसके दोनों हरों का योग परस्पर समान हो अथवा दोनों योग एक निश्चित अनुपात में हों तो किसी भी योग को शून्य समान रखने पर चर राशि का एक मान ज्ञात होता है।
अतः दोनों पक्षों के अंशों का योग = 2x + 4 + 2x + 1 = 4x + 5
दोनों पक्षों के हरों का योग = 2x + 1 + 2x + 4 = 4x + 5
दोनों समुच्चय समान हैं अतः 4x + 5 = 0
∴ \(x=\frac { -5 }{ 4 } \)
प्रश्न 16.
\(\frac { 3x+2 }{ 5x+7 } =\frac { x+1 }{ 3x-1 } \)
हल:
सूत्र चतुर्थ के अनुसार दोनों पक्षों के अंशों का योग
= 3x + 2 + x + 1
= 4x + 3 ……………..(i)
तथा हरों का योग = 5x +7 + 3x – 1 = 8x + 6
= 2 (4x + 3) …………..(ii)
दोनों योगों को अनुपात = 1 : 2
अतः सूत्रानुसार किसी भी योग को शून्य समान रखने पर
4x + 3 = 0
अतः 4 x = – 3
\(x=-\frac { 3 }{ 4 } \)
![]()
प्रश्न 17.
\(\frac { 5x+7 }{ 2x+1 } =\frac { x+1 }{ 3x+5 } \)
हल:
सूत्र पंचम-यदि समीकरण के एक पक्ष के अंश व (RBSESolutions.com) हर का अन्तर दूसरे पक्ष के अंश व हर के अन्तर के समान हो अथवा दोनों अन्तर एक निश्चित अनुपात में हों तो किसी भी अन्तर को शून्य समान रखने पर चर राशि का मान ज्ञात होता है।
वाम पक्ष के अंश व हर का अन्तर
5x + 7 – 2x – 1 = 3x + 6 …..(i)
दक्षिण पक्ष के अंश व हर का अन्तर
3x + 5 – 3 x – 1 = 2x + 4 ……..(ii)
अन्तर क्रमांक (i) व अन्तर क्रमांक (ii) का अनुपात = 3 : 2
अतः किसी भी अन्तर को शून्य समान रखने पर
2 x + 4 = 0
या , 2x = – 4
अतः \(x=\frac { -4 }{ 2 } =-2\)
![]()
प्रश्न 18.
\(\frac { 3x+6 }{ 6x+3 } =\frac { 5x+4 }{ 2x+7 } \)
हल:
वाम पक्ष के अंश वे हर का अन्तरे
6x + 3 – 3x – 6 = 3x – 3 ……..(i)
दक्षिण पक्ष के अंश व हर का अन्तरे
5x + 4 – 2x – 7 = 3x – 3 ……..(ii)
दोनों अन्तर समान हैं अतः
3x – 3 = 0
अतः \(x=\frac { 3 }{ 3 } =1\) उत्तर
∴ उपरोक्त प्रश्न द्विघात समीकरण है।
∴ इसका दूसरा मूल भी(RBSESolutions.com) ज्ञात करना है।
अब दोनों पक्षों के अंशों का योग = 3x + 6 + 5x +4
= 8x + 10
दोनों पक्षों के हरों का योग = 6x + 3 + 2x +7
= 8x + 10
∴ दोनों समान हैं
अतः 8x + 10 = 0
या 8x = -10
या \(x=\frac { -10 }{ 8 } =\frac { -5 }{ 4 } \)
अतः \(x=\frac { -5 }{ 4 } \) अथवा x = 1
![]()
प्रश्न 19.
\(\frac { 1 }{ x+2 } +\frac { 1 }{ x+6 } =\frac { 1 }{ x+1 } +\frac { 1 }{ x+7 } \)
हल:
सूत्र षष्ठ-यदि किसी समीकरण के प्रत्येक पक्ष में दो पद हों और (RBSESolutions.com) पदों का प्रत्येक अंश परस्पर समान हो तथा वाम पक्ष के हरों का योग दक्षिण पक्ष के हरों के योग के समान हो तो इस योग को शून्य के बराबर रखने पर चर राशि का मान प्राप्त होता है।
अतः यहाँ दोनों पक्षों के अंश संमान हैं।
वाम पक्ष के हरों का योग = (x + 2) + x + 6 = 2x + 8
x + 1 + x + 7 = 2x + 8
अतः 2x + 8 = 0
या 2 x = – 8
अतः \(x=\frac { -8 }{ 2 } =-4\)
![]()
प्रश्न 20.
\(\frac { 1 }{ x-4 } +\frac { 1 }{ x-6 } =\frac { 1 }{ x-2 } +\frac { 1 }{ x-8 } \)
हल:
दोनों पक्षों के अंश समान हैं । अतः
वाम पक्ष के हरों का योग = x – 4 + x – 6 = 2x – 10
दक्षिण पक्ष के हरों का योग = x – 2 + x – 8 = 2x – 10
सूत्रानुसार 2x – 10 = 0
या 2 x = 10
अतः \(x=\frac { 10 }{ 2 } =5\)
We hope the RBSE Solutions for Class 10 Maths Chapter 1 वैदिक गणित Ex 1.4 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 1 वैदिक गणित Exercise 1.4, drop a comment below and we will get back to you at the earliest.