RBSE Solutions for Class 10 Maths Chapter 11 Similarity Ex 11.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Exercise 11.2.
Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Ex 11.2
Ex 11.2 Class 10 RBSE Question 1.
D and E are to points on the (RBSESolutions.com) sides AB and AC of ΔABC, respectively. Such that DE || BC, then
(i) In AD = 6 cm, DB = 9 cm and AE = 8 cm then find AC.
(ii) If \(\frac { AD }{ DB }\) = \(\frac { 4 }{ 13 }\) and AC = 20.4 cm. Then find EC.
(iii) \(\frac { AD }{ DB }\) = \(\frac { 7 }{ 4 }\) and AE = 6.3 cm then find AC.
(iv) In AD = 4x – 3, AE = 8x – 7, BD = 3x – 1 and CE = 5x – 3 then find x.
Solution :
(i) In ∆ABC, DE || BC
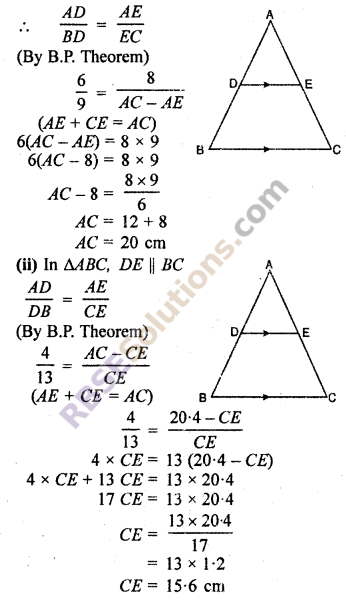
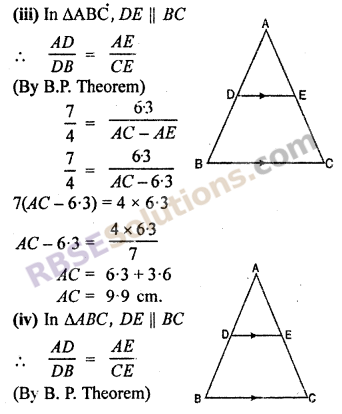

RBSE Solutions For Class 10 Maths Chapter 11.2 Question 2.
Points D and E lie on sides AB and AC of ΔABC, respectively. In (RBSESolutions.com) the following questions check whether DE || BC or not.
(i) AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
(ii) AB = 5.6 cm, AD = 1.4 cm, AC = 9.0 cm and AE = 1.8 cm
(iii) AD = 10.5 cm, BD = 4.5 cm, AC = 4.8 cm and AE = 2.8 cm
(iv) AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and EC = 5.5 cm
Solution :
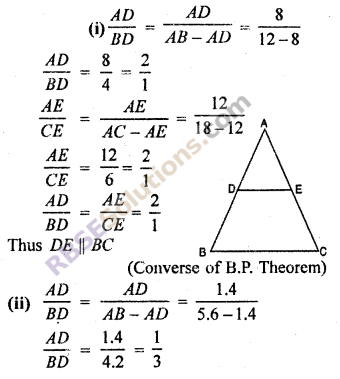
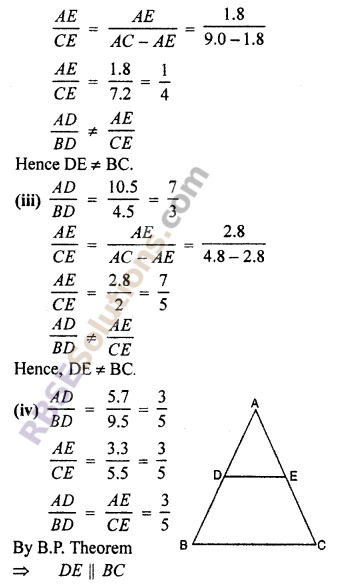
RBSE Class 10 Maths Chapter 11 Question 3.
In given figure, L, M and N are (RBSESolutions.com) points on OA, OB and OC such that LM || AM and MN || BC then show that LN || AC.
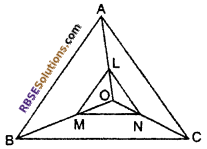
Solution :
Given : In ∆ABC, point L,M, N respectively lie OA, OB and OC such that LM || AB and MN || BC.
To prove : LN || AC
Proof : In ∆ABO
LM || AB (given)
\(\frac { OL }{ LA }\) = \(\frac { OM }{ MB }\) …..(ii) (By Basic prop. theorem)
Again, In ∆BCO
MN || BC
\(\frac { OM }{ MB }\) = \(\frac { ON }{ NC }\) ….(ii) (By Basc prop. theorem)
From equation (i) and (ii),
⇒ \(\frac { OL }{ LA }\) = \(\frac { OM }{ MB }\) = \(\frac { ON }{ NC }\)
\(\frac { OL }{ LA }\) = \(\frac { ON }{ NC }\) (By Converse of B. P. theorem)
⇒ LN || AC
RBSE Solutions For Class 10 Maths Chapter 11 Question 4.
In ∆ABC, D and E points lie on sides AB and AC such (RBSESolutions.com) that BD = CE. If ∠B = ∠C then show that DE || BC.
Solution :
In ∆ABC, D and E lie on sides BD = CE and ∠B = ∠C
To prove : DE || BC
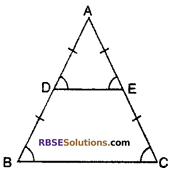
Proof : In ∆ABC,
∠B = ∠C
∴ AB = AC (opposite sides of equals angles are same)
⇒ AD + DB = AE + CE [∵ DB = CE given]
⇒ AD = AE
∵ ∠D = ∠E [Opposite angles of equal sides are same]
⇒ ∆ADE is an isosceles triangle
So, ∆ABC and ∆ADE are isosceles triangle in (RBSESolutions.com) which vertex angle ∠A is common in both triangles.
∴ ∠B = ∠C = ∠D = ∠E
∠B = ∠D [corresponding angle]
⇒ DE || BC
Exercise 11.2 Class 10 RBSE Question 5.
In fig. DE || BC and CD || EF then prove that : AD2 = AB × AF
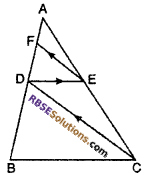
Solution :
Given : ∆ABC in (RBSESolutions.com) which DE || BC and CD || EF
To prove : AD2 = AB × AF
Proof : In ∆ABC
DE || BC


Ch 11 Class 10 Maths RBSE Question 6.
In fig., EF || DC || AB Then (RBSESolutions.com) prove that : \(\frac { AE }{ ED }\) = \(\frac { BF }{ FC }\)
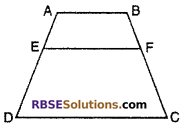
Solution :
Given : EF || DC || AB
To prove : \(\frac { AE }{ ED }\) = \(\frac { BF }{ FC }\)
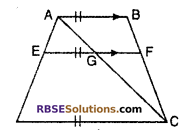
Construction : Join AC
Proof : In ∆ADC
GE || DC
∴ \(\frac { AE }{ ED }\) = \(\frac { AG }{ GC }\) ….(i) (By Basic proportionality theorem)
Now In ∆ABC
AB || GF
∴ \(\frac { CF }{ BF }\) = \(\frac { CG }{ AG }\) (By Basic Prop. Theorem)
or \(\frac { BF }{ CF }\) = \(\frac { AG }{ GC }\) ….(ii)
From equation (i) and (ii)
\(\frac { AE }{ ED }\) = \(\frac { BF }{ FC }\)
RBSE Class 10 Maths Chapter 11.2 Question 7.
ABCD is a parallelogram. P is any (RBSESolutions.com) point on side BC of ||gm. If DP and AB produced, meet at L then prove that:
(i) \(\frac { DP }{ PL }\) = \(\frac { DC }{ BL }\)
(ii) \(\frac { DL }{ DP }\) = \(\frac { AL }{ DC }\)
Solution :
Given : ABCD ¡s a parallelogram. Point P lies on side BC. Produced DP and AB meet at point L.
(i) To prove : \(\frac { DP }{ PL }\) = \(\frac { DC }{ BL }\)
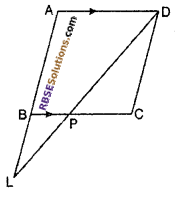
Proof : In ∆LDA
BP || AD
\(\frac { LP }{ DP }\) = \(\frac { LB }{ AB }\) (By B.P. Theorem)
or \(\frac { DP }{ PL }\) = \(\frac { DC }{ BL }\) [∵ AB = CD sides of ||gm]
⇒ \(\frac { DP }{ PL }\) = \(\frac { DC }{ BL }\)
(ii) To prove

11.2 Class 10 RBSE Question 8.
Point D and E lie on side AB of ∆ABC such (RBSESolutions.com) that AD = BE. If DP || BC and EQ || AC then prove that PQ || AB.
Solution :
Given : ∆ABC in which
AD = BE,
DP || BC and EQ || AC
To prove PQ || AB
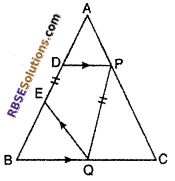
Proof : In ∆ABC DP || BC
\(\frac { AD }{ BD }\) = \(\frac { AP }{ CP }\) …..(i) (By B.P. Theorem)
and QE || AC
\(\frac { BE }{ AE }\) = \(\frac { BQ }{ QC }\) …..(ii)
∵ AD = BE (given) ……(iii)
AD + DE = BE + DE
AE = BD …..(iv)
putting values from (RBSESolutions.com) equation (iii) and (iv) in (ii)
\(\frac { BE }{ AE }\) = \(\frac { AD }{ BD }\) = \(\frac { BQ }{ QC }\)
From equation (i) and (v)
\(\frac { AP }{ DB }\) = \(\frac { AP }{ CP }\) = \(\frac { BQ }{ QC }\)
⇒ \(\frac { AP }{ CP }\) = \(\frac { BQ }{ QC }\)
⇒ \(\frac { CP }{ AP }\) = \(\frac { QC }{ BQ }\)
⇒ PQ || AB
10th Class Maths Chapter 11 Exercise 11.2 Question 9.
ABCD is a Trapezium in which AB || DC and its diagonals intersects each other at point O. Show that : \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\) (Higher Secondary Board Raj 2012)
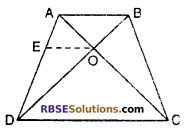
Solution :
Given : Trapezium ABCD in which AC and BC are (RBSESolutions.com) two diagonals which intersects each other at point O.
To prove : \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\)
Construction : From O, Draw OE || CD.
Proof : In ∆ADC
OE || DC
\(\frac { AE }{ ED }\) = \(\frac { AO }{ CO }\) ……(i) (By Basic prop. Theorem)
In Trapezium ABCD
AB || CD
OE || CD
OE || AB
Now, In ∆ABD
OE || AB
\(\frac { ED }{ AE }\) = \(\frac { DO }{ BO }\)
⇒ \(\frac { AE }{ ED }\) = \(\frac { BO }{ DO }\)
From equation (i) and (ii)
\(\frac { AO }{ CO }\) = \(\frac { BO }{ DO }\)
⇒ AO × DO = BO × CO
⇒ \(\frac { AO }{ BO }\) = \(\frac { CO }{ DO }\)
Exercise 11.2 Class 10 Question and Answer Question 10.
Points D and E lie on sides AB and AC of ∆ABC such (RBSESolutions.com) that BD = CE then show that ∆ABC Is isosceles triangles.
Solution :
Given : In ∆ABC, D and E lie on sides AB and AC such that BD = CE.
To prove : ∆ABC is an isosceles triangle.
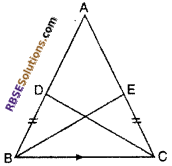
Construction : Join DC and BE.
Proof : In ∆BCD and ∆BEC
BD = CE (given)
∠BDC = ∠BEC [∵ angles of same base an some height]
BC = BC (common)
By SAS rule ∆BCD = ∆BEC
∴ ∠ABC = ∠ACE (by CPCT)
⇒ AB = AC (Sides opposite to (RBSESolutions.com) equal angles are same)
Hence ∆ABC is an isosceles triangle.
We hope the given RBSE Solutions for Class 10 Maths Chapter 11 Similarity Ex 11.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 11 Similarity Exercise 11.2, drop a comment below and we will get back to you at the earliest.