RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2

RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 13 Circle and Tangent Exercise 13.2.

Rajasthan Board RBSE Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2

Question 1.
According to figure, answer (RBSESolutions.com) the following questions :
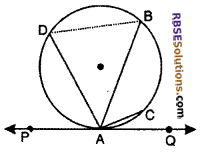
RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 1
(i) ∠BAQ is an alternate segment of circle.
(ii) ∠DAP is an alternate segment of circle.
(iii) If C is joined with B, then ∠ACB is equal to which angle?
(iv) ∠ABD and ∠ADB is equal to which angles.
Solution :
(i) Alternate segment of ∠BAQ = ADB
(ii) Alternate segement of ∠DAP = ACBD
(iii) ∠ACB = ∠BAP
(iv) ∠ABD = ∠DAP and ∠ADB = ∠BAQ

Question 2.
According to (RBSESolutions.com) figure, if ∠BAC = 80°, then find the value of ∠BCP.
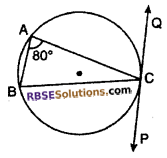
RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 2
Solution :
We know that
∵ Alternate segment of ∠BCP = ∠BAC
∴ ∠BCP = ∠BAC
⇒ ∠BCP = 80°

Question 3.
According to figure, PQ and XY are (RBSESolutions.com) parallel tangents. If ∠QRT = 30°, then find the value of ∠TSY.
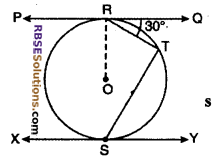
RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 3
Solution :
Given :
PQ || XY

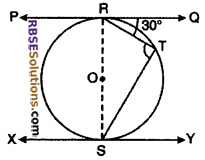
and ∠QRT = 30°
Diameter of circle (RBSESolutions.com) of centre O is RS
∴ OR ⊥ PR and OS ⊥ XY
∴ ∠QRO = 90°
⇒ ∠QRS = 90°
∠RTS = ∠QRS – ∠QRT
= 90° – 30° = 60°
∴ ∠TRS = 60°
Now ∠TSY = ∠TRS
⇒ ∠TSY = 60°

Question 4.
Figure, in a cyclic quadrilateral ABCD diagonal AC bisects the angle C. Then prove that (RBSESolutions.com) diagonal BD is parallel to tangent PQ of a circle which passes through the points A.
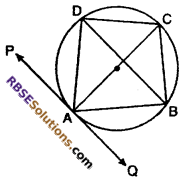
RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 5
Solution :
Given :
∠ACD = ∠ACB
Now, we can see here
that ∠PAD = ∠ABD (∵ angle in the alternate segment)
similarly ∠QAB = ∠ADB
Also AB is a (RBSESolutions.com) common arc. ADB and ACB are the angle in the same segment.
∴ ∠ADB = ∠ACD
similarly, ∠ABD = ∠ACD
By equation (i), we find that
∠PAD = ∠ADB (alternate interior angle)
∴ PQ || BD

We hope the given RBSE Solutions for Class 10 Maths Chapter 13 Circle and Tangent Ex 13.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 13 Circle and Tangent Exercise 13.2, drop a comment below and we will get back to you at the earliest.