RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Exercise 15.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 15 |
| Chapter Name | Circumference and Area of a Circle |
| Exercise | Exercise 15.1 |
| Number of Questions Solved | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1
RBSE Solutions For Class 10 Maths Chapter 15.1 Question 1.
The radius of a circle is 3.5 cm. Find (RBSESolutions.com) its area and circumference.
Solution :
Given :
Radius of circle (r) = 3.5 cm
Circumference of circle = 2πr
= 2 × \(\frac { 22 }{ 7 }\) × 3.5
= 22 cm
Area of circle = πr2
= \(\frac { 22 }{ 7 }\) × (3.5) × (3.5)
= 38.5 cm2
Thus, circumference of circle is 22 cm and area is 38.5 cm2
15.1 Class 10 RBSE Question 2.
The circumference of a circle Is 44 m. Find (RBSESolutions.com) area of circle.
Solution :
Given
Circumference = 44 m
Let radius of circle = r m
Thus, 2πr = 44
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 44
⇒ r = \(\frac { 44\times 7 }{ 2\times 22 } \)
= 7 m
Area of circle = πr2
= \(\frac { 22 }{ 7 }\) × 7 × 7
= 154 m2
Thus, area of circle is 154 m2
Ex 15.1 Class 10 RBSE Question 3.
The radius of a semicircular plot is 21 m. Find (RBSESolutions.com) its area and perimeter.
Solution :
Given :
Radius of semi-circular plot
(r) = 21 m
Area = \(\frac { 1 }{ 2 }\)πr2
= \(\frac { 1 }{ 2 }\) × \(\frac { 22 }{ 7 }\) × 21 × 21
= 693 m2
and perimeter = \(\frac { 1 }{ 2 }\) × 2πr + 2r
= πr + 2r
= \(\frac { 22 }{ 7 }\) × 21 + 2 × 21
= 66 + 42
= 108 m
Thus, area of plot ¡s 693 m2 and perimeter is 108 m
RBSE Solutions For Class 10 Maths Chapter 15 Question 4.
The wheel of scooter covered 88 m distance in 100 revolution. Find (RBSESolutions.com) the radius of wheel
Solution :
Given :
In 100 revolutions, wheel covered a distance of 88 m.
Distance covered by wheel in 1 rotation = circumference of wheel

= \(\frac { 14 }{ 100 }\) m
= \(\frac { 14 }{ 100 }\) × 100 cm
= 14 cm
Thus, radius of wheel = 14 cm
Exercise 15.1 Class 10 RBSE Question 5.
The area of a circular plate is 154 cm2. Find (RBSESolutions.com) its circumference.
Solution :
Given :
Area of circular = 154 cm2
Lei radius of plate i.s r cm, then
πr2 = 154
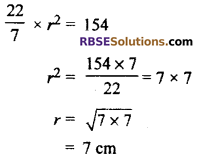
Circumference of circular plate = 2πr
= 2 × \(\frac { 22 }{ 7 }\) × 7
= 44 cm
Thus, Circumference of circular plate = 44 cm
RBSE Class 10 Maths Chapter 15 Question 6.
The circumference of circle is equal to perimeter of a (RBSESolutions.com) square. If area of square is 484 sq m, then find the area of circle.
Solution:
Let side of square = x m
then perimeter of square 4 × x
and area of square = x2
According to question
Area of square =484 sq m
x2 = 484
x = \(\sqrt { 484 }\)
= 22 m
Perimeter of square = 4x = 4 × 22 = 88 m
Let radius of circle is r
circumference of circle = perimeter of square
⇒ 2πr = 88
⇒ 2 × \(\frac { 22 }{ 7 }\) × r = 88
r = \(\frac { 88\times 7 }{ 2\times 22 } \) = 14 m
Thus, area of the circle = πr2
= \(\frac { 22 }{ 7 }\) × 14 × 14 = 616 sq m.
Thus, area of the circle = 616 sq m.
RBSE Class 10 Maths Chapter 15 Solutions Question 7.
The cost of fencing a circular field at (RBSESolutions.com) the rate 24 per meter is ₹ 5280 and rate of ploughing is ₹ 0.50 per meter. Find the cost of ploughing the field.
Solution :
Cost of fencing at the rate ₹ 24 per m = ₹ 5280
Let, radius of circular field = r m
Thus, circumference of circular field

Thus, radius of circular field = 35 m
Area of circular field = πr2
= \(\frac { 22 }{ 7 }\) × 35 × 35 = 3850 sq. m.
∵ cost of ploughing the field 1 m2 = ₹ 0.50
∴ cost of ploughing the field 3850 sq. m.
= 0.50 × 3850 = ₹ 1925
Thus, cost of ploughing the plot = ₹ 1925
RBSE Class 10 Maths Chapter 15.1 Question 8.
The radius of a circular grass (RBSESolutions.com) field in 35 m. There is 7 m wide ramp around it. Find the area of ramp.
Solution :
Given :
Radius of circular grass field = 35 m.
Width of ramp = 7 m.
R = 35 + 7 = 42 m
Thus area of ramp
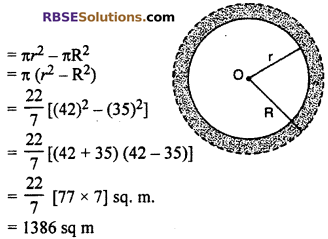
Thus, area of ramp is 1694 sq m
Circumference Of A Circle And Area Class 10 Question 9.
The area between two (RBSESolutions.com) concentric circles will be :
(A) πR2
(B) π (R + r)(R – r)
(C) π(R2 – r)
(D) None of these
Solution :
= πR2 – πr2
= π(R2 – r2)
= π (R + r)(R – r)
Thus, option (B) is correct.
Ch 15 Class 10 Maths RBSE Question 10.
Radius of two concentric circles (RBSESolutions.com) are 4 cm and 3 cm respectively. Then area bounded by these circles will be:
(A) 22 cm2
(B) 12 cm2
(C) 32 cm2
(D) 18 cm2
Solution :
Given : Radius of two concentre circle are 4 cm and 3 cm.
Thus, R= 4 cm, r = 3 cm
∴ Area between two concentric circles
= π(R2 – r2)
= \(\frac { 22 }{ 7 }\) [(4)2 – (3)2]
= \(\frac { 22 }{ 7 }\) × [(4 + 3) (4 – 3)]
= \(\frac { 22 }{ 7 }\) × 7 = 22 cm2
Thus option (A) is correct.
We hope the given RBSE Solutions for Class 10 Maths Chapter 15 Circumference and Area of a Circle Ex 15.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 15 Circumference and Area of a Circle Exercise 15.1, drop a comment below and we will get back to you at the earliest.