RBSE Solutions for Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | पृष्ठीय क्षेत्रफल एवं आयतन |
| Exercise | Additional Questions. |
| Number of Questions Solved | 72 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions
विविध प्रश्नमाला 16
प्रश्न 1.
एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 486 वर्ग सेमी. है। (RBSESolutions.com) घन की भुजा, होगी
(क) 6 सेमी.
(ख) 8 सेमी.
(ग) 9 सेमी.
(घ) 7 सेमी.
उत्तर:
(ग) 9 सेमी.
प्रश्न 2.
एक घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 9 मीटर, 2 मीटर और 1 मीटर है। घनाभ का पृष्ठीय क्षेत्रफल होगा
(क) 12 वर्ग मीटर
(ख) 11 वर्ग मीटर
(ग) 21 वर्ग मीटर
(घ) 22 वर्ग मीटर
उत्तर:
(घ) 22 वर्ग मीटर
प्रश्न 3.
एक गोले का व्यास 6 सेमी. है। गोले का (RBSESolutions.com) आयतन होगा
(क) 16 π घन सेमी.
(ख) 20 π घन सेमी.
(ग) 36 π घन सेमी.
(घ) 30 π घन सेमी.
उत्तर:
(ग) 36 π घन सेमी.
![]()
प्रश्न 4.
एक बेलन के आधार की त्रिज्या 14 सेमी. तथा ऊँचाई 10 सेमी. है। बेलन का वक्र पृष्ठ होगा
(क) 810 सेमी2.
(ख) 880 सेमी2.
(ग) 888 सेमी2.
(घ) 890 सेमी2.
उत्तर:
(ख) 880 सेमी2.
प्रश्न 5.
एक शंकु का आयतन 308 सेमी. और ऊँचाई 6 सेमी. है। (RBSESolutions.com) उसके आधार की त्रिज्या होगी
(क) 7 सेमी.
(ख) 8 सेमी.
(ग) 6 सेमी.
(घ) इनमें से कोई नहीं
उत्तर:
(क) 7 सेमी.
प्रश्न 6.
एक ठोस धातु के अर्ध गोले का व्यास 42 सेमी. है। इसके सम्पूर्ण पृष्ठ पर 20 पैसे प्रति वर्ग सेमी. की दर से पॉलिश कराने का व्यय ज्ञात कीजिए।
हल:
अर्ध गोले का व्यास = 42 सेमी.
तब अर्ध गोले की त्रिज्या \((r)=\frac{42}{2}=21\) सेमी.
अर्ध गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 3πr2

अर्ध गोले के सम्पूर्ण पृष्ठ पर 20 पैसे प्रति वर्ग सेमी. की दर से (RBSESolutions.com) पॉलिश कराने की व्यय = 20 x 4150 पैसे = 0.20 x 4158 रुपये।
= ₹ 831.60 उत्तर
प्रश्न 7.
एक शंकु, एक अर्द्ध गोला व एक बेलन एक ही आधार और ऊँचाई पर बने हैं। उनके आयतनों का अनुपात लिखिए।
हल:
∴ एक शंकु, एक अर्द्ध गोला और एक बेलन एक ही आधार और ऊँचाई पर बने हैं।
∴ आधार तथा ऊँचाई को x मानने पर अर्थात् h = r = x (माना)
एक शंकु का आयतन होगा \(=\frac{1}{3} \pi r^{2} h=\frac{1}{3} \pi x^{3}\)
एक अर्द्ध गोले का आयतन होगा \(=\frac{2}{3} \pi r^{3}=\frac{2}{3} \pi x^{3}\)
एक बेलन का आयतन होगा = πr2h = πx3.
तीनों के आयतन को अनुपात होगा =

अतः तीनों के आयतन का क्रमशः अनुपात होगा 1 : 2 : 3 उत्तर
प्रश्न 8.
एक ठोस पिण्ड का बायां भाग बेलनाकार और दायां भाग शंकुनुमा है। (RBSESolutions.com) यदि बेलन का व्यास 14 सेमी. तथा लंबाई 40 सेमी. और शंकु का व्यास 14 सेमी. तथा उसकी ऊँचाई 12 सेमी. हो, तो ठोस का आयतन ज्ञात कीजिए।
हल:
बेलन का आयतन + शंकु का आयतन = ठोस का आयतन

ठोस का आयतन = 6776 सेमी3. उत्तर
![]()
प्रश्न 9.
9 सेमी. त्रिज्या के धातु के गोले को पिघलाकर 3 सेमी. त्रिज्या और 6 सेमी. ऊँचाई के शंकु बनाए जा सकते हैं। (RBSESolutions.com) शंकुओं की संख्या ज्ञात करो।
हल:
9 सेमी. त्रिज्या वाले गोले का आयतन
\(=\frac{4}{3} \pi r^{3}\)

3 सेमी. त्रिज्या व 6 सेमी. ऊँचाई वाले शंकु का आयतन
\(=\frac{1}{3} \pi r^{2} h\)
\(\begin{array}{l}{=\frac{1}{3} \pi(3)^{2}(6)} \\ {=\frac{\pi \times 3 \times 3 \times 6}{3}}\end{array}\)
18π घन सेमी.
धातु के गोले को पिघलाकर बन सकने वाले शंकुओं की संख्या

अतः बने शंकुओं की संख्या = 54 उत्तर
प्रश्न 10.
एक गाँव जिसकी जनसंख्या 4000 है, जिसको प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। (RBSESolutions.com) इस गाँव में 20 मीटर × 15 मीटर × 6 मीटर माप वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा?
हल:
टंकी की माप = 20 मीटर × 15 मीटर × 6 मीटर
टंकी का आयतन = 20 × 15 × 6 मीटर3
= 1800 मीटर3
हम जानते हैं 1 मीटर3 = 1000 लीटर
इसलिये 1800 मीटर3 = 1800 × 1000
= 1809000 लीटर
गाँव की जनसंख्या = 4000
गाँव को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है अतः पानी की टंकी का पानी वहाँ काम आएगा।

प्रश्न 11.
क्रमशः 6 सेमी., 8 सेमी. और 10 सेमी. त्रिज्याओं वाले धातु के तीन ठोस गोलों को (RBSESolutions.com) पिघलाकर एक बड़ा गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
हल:
पहले गोले की त्रिज्या (r1) = 6 cm.
दूसरे गोले की त्रिज्या (r2) = 8 cm.
तीसरे गोले की त्रिज्या (r3) = 10 cm.
माना कि नए बने गोले की त्रिज्या = R cm.
तीनों गोलों का आयतन = बड़े गोले का आयतन
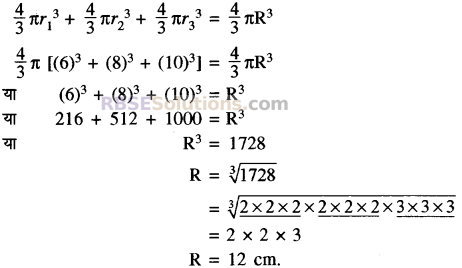
अतः बड़े गोले की त्रिज्या = 12 cm. उत्तर
प्रश्न 12.
एक शंकु के आकार की बर्तन की त्रिज्या 10 सेमी. और ऊँचाई 18 सेमी. है। (RBSESolutions.com) पानी से पूरा भरा हुआ है। इसे 5 सेमी. त्रिज्या के एक बेलनाकार बर्तन में उँडेला जाता है। बेलनाकार बर्तन में पानी की ऊँचाई ज्ञात कीजिए।
हल:
शंकु के आकार के बर्तन की त्रिज्या (r) = 10 सेमी.
ऊँचाई (h) = 18 सेमी.
शंकु का आयतन
\(\begin{array}{l}{=\frac{1}{3} \pi r^{2} h} \\ {=\frac{1}{3} \times \pi \times 10 \times 10 \times 18}\end{array}\) घन सेमी.
= π × 100 × 6 घन सेमी.
= 600 π घन सेमी.
∴ इस आयतन के पानी को बेलनाकार बर्तन में डाला जाता है।
∴ बेलन का आयतन = πr2h अर्थात्
πr2h = 600
\(\begin{aligned} \mathrm{h} &=\frac{600 \pi}{\pi \times 5 \times 5} \\ \mathrm{h} &=\frac{600}{25}=24 \end{aligned}\) सेमी.
∴ बेलनाकार बर्तन में पानी की ऊँचाई 24 सेमी. होगी। उत्तर
प्रश्न 13.
यदि 11 सेमी. × 3.5 सेमी. × 2.5 सेमी. मोम के.एक घनाभ से 2.8 सेमी. व्यास की (RBSESolutions.com) एक मोमबत्ती बनाई जाती है। मोमबत्ती की लम्बाई ज्ञात कीजिए।
हल:
घनाभाकार मोमबत्ती का आयतन = (ल. × चौ. × ॐ.) घन सेमी.
= 11 × 3.5 × 2.5 घन सेमी.
अब बेलनाकार मोमबत्ती का आयतन = π2rh
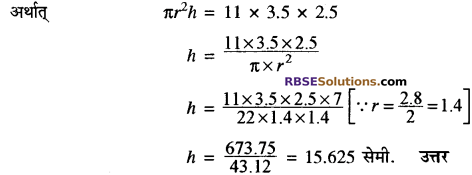
![]()
प्रश्न 14.
धातु के एक गोले का व्यास 6 सेमी. है। गोले को पिघलाकर एक समान वृत्तीय अनुप्रस्थ-परिच्छेद वाला तार बनाया गया है। यदि तार की लम्बाई 36 मीटर हो, तो उसकी त्रिज्या ज्ञात कीजिए।
हल:
∴ गोले का व्यास = 6 सेमी.
त्रिज्या \((\mathrm{r})=\frac{6}{2}=3\) सेमी.
गोले का आयतन \(=\frac{4}{3} \pi r^{3}\) घन इकाई
\(=\frac{4}{3} \times \frac{22}{7} \times(3)^{3}\) घन सेमी.
तथा बेलन का आयतन = πr2h
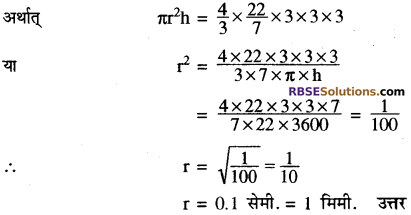
अन्य महत्त्वपूर्ण प्रश्न
वस्तुनिष्ठ प्रश्न
प्रश्न 1.
एक घन की कोर 4 सेमी. है। (RBSESolutions.com) इसके विकर्ण की लम्बाई है
(क) 12 सेमी.
(ख) \(8 \sqrt{3}\) सेमी.
(ग) \(6 \sqrt{3}\) सेमी.
(घ) \(4 \sqrt{3}\) सेमी.
उत्तर:
(घ) \(4 \sqrt{3}\) सेमी.
प्रश्न 2.
लकड़ी के एक बन्द संदूक की बाह्य लम्बाई, चौड़ाई व ऊँचाई क्रमशः 20 सेमी., 16 सेमी. व 12 सेमी. है। यदि लकड़ी की मोटाई 1 सेमी. हो, तो लकड़ी का आयतन होगा
(क) (20 × 16 × 12 – 18 × 14 × 10) सेमी3.
(ख) (20 × 16 × 12 – 19 × 15 × 11) सेमी3.
(ग) (22 × 18 × 14 – 20 × 16 × 12) सेमी3.
(घ) (21 × 17 × 13 – 20 × 16 × 12) सेमी3.
उत्तर:
(क) (20 × 16 × 12 – 18 × 14 × 10) सेमी3.
प्रश्न 3.
एक घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 4 सेमी., 2 सेमी. तथा 1 सेमी. है (RBSESolutions.com) तो उसका सम्पूर्ण पृष्ठीय क्षेत्रफल होगा
(क) 7 वर्ग सेमी.
(ख) 8 वर्ग सेमी.
(ग) 14 वर्ग सेमी.
(घ) 28 वर्ग सेमी.
उत्तर:
(घ) 28 वर्ग सेमी.
प्रश्न 4.
8 मीटर भुजा वाली एक वर्गाकार दीवार में 40 सेमी. x 20 सेमी. वाली कितनी टाइल्स लगेंगी?
(क) 800
(ख) 100
(ग) 6400
(घ) 51200
उत्तर:
(क) 800
प्रश्न 5.
एक आयताकार टंकी के पेंदे का क्षेत्रफल 20 वर्ग मीटर है। इस टंकी में 25 सेमी. ऊँचाई तक पानी भरा है। (RBSESolutions.com) टंकी में पानी का आयतन होगा
(क) 20 × 25 घन मीटर
(ख) \(20 \times \frac{1}{4}\) घन मीटर
(ग) 20 × 20 × 25 घन मीटर
(घ) \(20 \times 20 \times \frac{1}{4}\) घन मीटर
उत्तर:
(ख) \(20 \times \frac{1}{4}\) घन मीटर
![]()
प्रश्न 6.
यदि किसी शंकु की ऊँचाई एवं त्रिज्या क्रमशः 12 सेमी. और 5 सेमी. हैं तो इसके वक्र पृष्ठ का क्षेत्रफल है
(क) 60 π सेमी.2
(ख) 65 π सेमी.2
(ग) 100 π सेमी.2
(घ) 120 π सेमी.2
उत्तर:
(ख) 65 π सेमी.2
प्रश्न 7.
2 सेमी. व्यास वाले ठोस कांच के एक अर्द्ध गोले (RBSESolutions.com) का संपूर्ण पृष्ठीय क्षेत्रफल
(क) 127 सेमी.2
(ग) 37. सेमी.2
(ख) 87 सेमी.2
(घ) 27 सेमी.2
उत्तर:
(ग) 37. सेमी.2
प्रश्न 8.
एक गोले का व्यास 1 है, तो गोले का आयतन होगा
(क) \(\frac{4}{3} \pi d^{3}\)
(ख) \(\frac{\pi}{6} d^{3}\)
(ग) 4πd2
(घ) πd2
उत्तर:
(ख) \(\frac{\pi}{6} d^{3}\)
प्रश्न 9.
एक ठोस गोले की त्रिज्या, वक्र पृष्ठ का क्षेत्रफल और आयतन क्रमश: r, S व V हैं, (RBSESolutions.com) उनके बीच में निम्न में से सही संबंध होगा
(क) 3r = VS
(ख) 3rS = V
(ग) 3rV = S
(घ) 3V = rS
उत्तर:
(घ) 3V = rS
प्रश्न 10.
समान त्रिज्या वाले एक गोले तथा एक अर्द्ध गोले के संपूर्ण पृष्ठीय क्षेत्रफल में अनुपात होगा
(क) 1 : 2
(ख) 2 : 1
(ग) 3 : 4
(घ) 4 : 3
उत्तर:
(घ) 4 : 3
अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
एक बन्दं लकड़ी के बक्से की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 90 सेमी., 50 सेमी. और 30 सेमी. है। (RBSESolutions.com) बक्से का बाहरी पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
बक्से की लम्बाई = 90 सेमी.
बक्से की चौड़ाई = 50 सेमी.
बक्से की ऊँचाई = 30 सेमी.
बक्से का बाहरी सम्पूर्ण पृष्ठीय क्षेत्रफल

![]()
प्रश्न 2.
एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 1014 वर्ग मीटर है। घन की भुजा ज्ञात कीजिए।
हल:
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 1014 वर्ग मीटर
माना घन की भुजा = x मीटर
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6(भुजा)2
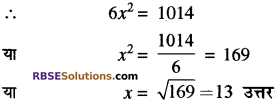
प्रश्न 3.
यदि घनाभ की लम्बाई 12 मीटर, चौड़ाई 9 मीटर और ऊँचाई 8 मीटर है (RBSESolutions.com) तो घनाभ के विकर्ण की लम्बाई ज्ञात कीजिए।
हल:
घनाभ की लम्बाई = 12 मीटर
घनाभ की चौड़ाई = 9 मीटर
घनाभ की ऊँचाई = 8 मीटर।
हम जानते हैं कि घनाभ का विकर्ण

प्रश्न 4.
एक घन की समस्त कोरों की लम्बाइयों का योग 12 सेमी. है। घन का आयतन लिखिए।
हल:
घन की समस्त कोरों की संख्या = 12
अतः प्रत्येक कोर की लम्बाई = 1 सेमी.
घन का आयतन = 1 × 1 × 1
= 1 घन सेमी. उत्तर
प्रश्न 5.
एक घनाकार डिब्बे का आयतन 64 घन सेमी. है। (RBSESolutions.com) डिब्बे की प्रत्येक कोर (भुजा) की नाप लिखिए।
हल:
भुजा \(=\sqrt[3]{64}=\left(4^{3}\right)^{1 / 3}=4\) सेमी. उत्तर
प्रश्न 6.
एक घन मीटर में कितने लीटर होते हैं? लिखिए।
उत्तर:
1000 लीटर।
प्रश्न 7.
एक कमरे की चारों दीवारों का क्षेत्रफल 30 मी. है। कमरे की ऊँचाई 3 मीटर है। कमरे के फर्श का परिमाप लिखिए।
हल:
परिमाप \(=\frac{30}{3}=10\) मीटर
प्रश्न 8.
यदि एक अर्द्धगोले का संपूर्ण पृष्ठीय क्षेत्रफल 487 वर्ग सेमी. है तो इसके त्रिज्या की लम्बाई लिखिए।
हल:
यहाँ
\(\begin{aligned} 3 \pi r^{2} &=48 \pi \\ r^{2} &=\frac{48 \pi}{3 \pi}=16 \end{aligned}\)
अतः त्रिज्या \(=\sqrt{16}=4\) सेमी. उत्तर
![]()
प्रश्न 9.
एक बेलन के आधार की त्रिज्या 7 सेमी. तथा ऊँचाई 5 सेमी. है। (RBSESolutions.com) बेलन के वक्रपृष्ठ का क्षेत्रफल लिखिए।
हल:
बेलन का वक्रपृष्ठ क्षेत्रफल = 2πrh
r = 7 सेमी. तथा
h = 5 सेमी.
∴ वक्रपृष्ठ का क्षेत्रफल \(=2 \times \frac{22}{7} \times 7 \times 5\) वर्ग सेमी.
= 220 वर्ग सेमी. उत्तर
प्रश्न 10.
यदि एक गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल 36 सेमी. है तो उसकी त्रिज्या ज्ञात कीजिए।
हल:
गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल
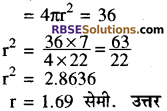
r = 1.69 सेमी. उत्तर
प्रश्न 11.
एक बेलन की त्रिज्या 7 सेमी. और ऊँचाई 15 सेमी. है। (RBSESolutions.com) बेलन के वक्रपृष्ठ का क्षेत्रफल लिखिए।
हल:
\(2 \times \frac{22}{7} \times 7 \times 15=660\) वर्ग सेमी. उत्तर
प्रश्न 12.
एक बेलन जिसकी ऊँचाई 3 सेमी. है तथा बेलन का वक्रपृष्ठ 66 सेमी.2 है, तो उसकी त्रिज्या लिखिए।
हल:
बेलन का वक्र पृष्ठ = 2πrh
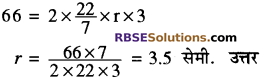
प्रश्न 13.
एक घन का सम्पूर्ण पृष्ठीय क्षेत्रफल 216 वर्ग मीटर है। घन की भुजा ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, 2018)
हल:
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 216 वर्ग मीटर
घन की भुजा = ?
घन का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6 × (भुजा)2
216 = 6 × (भुजा)2
(भुजा)2 \(=\frac{216}{6}=36\)
∴ भुजा \(=\sqrt{36}=6\) मीटर
अतः घन की भुजा = 6 मीटर उत्तर
प्रश्न 14.
एक अर्द्ध गोले की त्रिज्या 7 सेमी. है, (RBSESolutions.com) इसका सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (माध्य, शिक्षा बोर्ड, 2018)
हल:
दिया है–
r = 7 सेमी.
अर्द्ध गोले का सम्पूर्ण पृष्ठीय क्षेत्रफल = 3πr2
मान रखने पर
\(=3 \times \frac{22}{7} \times 7 \times 7=462\) वर्ग सेमी. उत्तर
लघूत्तरात्मक प्रश्न
प्रश्न 1.
एक घन की कोर 5 सेमी. है। (RBSESolutions.com) इसके किसी एक तल के विकर्ण की लम्बाई ज्ञात कीजिए।
हल:
घन के एक तल का विकर्ण
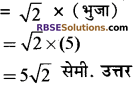
प्रश्न 2.
25 सेमी. × 20 सेमी. × 16 सेमी. माप के सीसे के एक घन को पिघलाकर एक नया घन बनाया जाता है, तो इस घन की कोर ज्ञात कीजिए।
हल:
घन का आयतन = 25 × 20 × 16 सेमी.2
घन की भुजा कोर
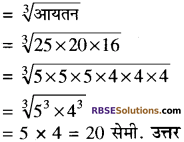
![]()
प्रश्न 3.
एक घनाभ की लम्बाई, चौड़ाई और ऊँचाई में 6 : 5 : 4 का अनुपात है। (RBSESolutions.com) यदि उसका आयतन 960 घनसेमी. है तो घनाभ की लम्बाई, चौड़ाई तथा ऊँचाई ज्ञात कीजिये।
हल:
∴ माना घनाभ की लम्बाई 6x, चौड़ाई 5x तथा ऊँचाई 4x है।
∴ घनाभ का आयतन = 6x × 5x × 4x
अर्थात् 6x × 5x × 4x = 960 घन सेमी.
120x3 = 960 घन सेमी.
\(\Rightarrow \quad x^{3}=\frac{960}{120}=8 \quad 41 x=\sqrt[3]{8}=2\) सेमी.
∴ घनाभ की लम्बाई = 6x = 6 × 2 = 12 सेमी.
घनाभ की चौड़ाई = 5x = 5 × 2 = 10 सेमी.
घनाभ की ऊँचाई = 4x = 4 × 2 = 8 सेमी. उत्तर
प्रश्न 4.
दो गोलों के पृष्ठीय क्षेत्रफलों का अनुपात 4:9 है। (RBSESolutions.com) उनके पृष्ठीय त्रिज्याओं एवं आयतनों का अनुपात ज्ञात कीजिए।
हल:
माना दो गोलों की त्रिज्याएँ r1 और r2 हैं। उनके पृष्ठीय क्षेत्रफल \(4 \pi r_{1}^{2}\) तथा \(4 \pi r_{2}^{2}\) हैं।
गोलों के पृष्ठीय क्षेत्रफलों का अनुपात
\(=\frac{4 \pi r_{1}^{2}}{4 \pi r_{2}^{2}}=\frac{4}{9}\)
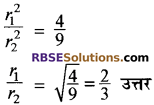
दो गोलों के पृष्ठीय क्षेत्रफलों का अनुपात
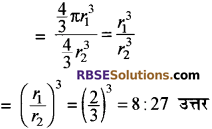
प्रश्न 5.
एक कक्ष की लम्बाई 5 मीटर, चौड़ाई 3.5 मीटर व ऊँचाई 4 मीटर है। 20 रु. प्रति वर्गमीटर की दर से चारों दीवारों पर सफेदी कराने का व्यय ज्ञात कीजिए।
हल:
कमरे की लम्बाई = 5 मीटर
चौड़ाई = 3.5 मीटर
ऊँचाई = 4 मीटर
कमरे की चारों दीवारों का क्षेत्रफल = 2(लम्बाई + चौड़ाई) ऊँचाई
= 2(5 + 3.5) × 4
= 2 × 8.5 × 4
= 68 वर्ग मीटर
चारों दीवारों पर सफेदी कराने का व्यय ₹ = 68 × 20
या व्यय ₹ = 1360 उत्तर
प्रश्न 6.
घन के एक पृष्ठ का परिमाप 28 सेमी. है (RBSESolutions.com) तो घन का आयतन ज्ञात कीजिए।
हल:
घेने के एक पृष्ठ का परिमाप = 28 सेमी.
∴ घन की सभी भुजाएँ बराबर होती हैं।
∴ घन के एक पृष्ठ का परिमाप = 4 × भुजा
या 28 = 4 × भुजा
भुजा \(=\frac{28}{4}=7\) सेमी.
घन का आयतन = (भुजा)3 = (7)3
= 7 × 7 × 7 = 343 घन सेमी. उत्तर
प्रश्न 7.
दो घनों, जिनमें से प्रत्येक का आयतन 27 सेमी.3 है, के संलग्न फलकों को मिलाकर एक ठोस बनाया जाता है। (RBSESolutions.com) प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
माना कि घन की प्रत्येक भुजा = x cm. है।
घन का आयतन = 27 cm.3

∴ घन की भुजा = 3 cm.
∴ दोनों घनों को जोड़ने पर वह घनाभ बन जाएगा।
इसकी लम्बाई = 2x cm. = 2 × 3 = 6 cm.
चौड़ाई = x = 3 cm.
तथा ऊँचाई = x = 3 cm.
अब घनाभ का पृष्ठीय क्षेत्रफल
= 2 [लं. × चौ. + चौ. × ऊँ. + ऊँ. × लं.]
= 2 [6 × 3 + 3 × 3 + 3 × 6]
= 2 [18 + 9 + 18]
= 2 [45]
= 90 cm.2
अर्थात् घनाभ का क्षेत्रफल 90 cm.2 है। उत्तर
![]()
प्रश्न 8.
धातु के तीन समान घनों की कोर क्रमशः 3 सेमी., 4 सेमी., 5 सेमी. है। (RBSESolutions.com) इन्हें पिघलाकर एक नया घन बनाया गया। इस घन की कोर की – लम्बाई ज्ञात कीजिये।
हल:
3 सेमी. कोर वाले घन का आयतन = (भुजा)3 = (3)3 = 27 घन सेमी.
4 सेमी. कोर वाले धन का आयतन = (भुजा)3 = (4)3 = 64 घन सेमी.
5 सेमी. कोर वाले घन का आयतन = (भुजा)3 = (5)3 = 125 घन सेमी.
इन घनों का सम्पूर्ण आयतन = 27 + 64 + 125 = 216 सेमी.3
इन्हें पिघलाकर नया घन बनाया गया है।
अतः नये घन का आयतन = 216 घन सेमी.
(भुजा)3 = 216
भुजा \(=\sqrt[3]{216}\)
भुजा \(=(6 \times 6 \times 6)^{1 / 3}\)
भुजा \(=6^{3 \times 1 / 3}=6\)
अतः नये घन की कोर = 6 सेमी. उत्तर
प्रश्न 9.
एक सन्दूक की माप 3 मी. × 2 मी. × 1.80 मी. है। (RBSESolutions.com) बाहर की ओर सभी फलकों पर ₹ 12 प्रति वर्ग मीटर की दर से वार्निश कराने का व्यय ज्ञात कीजिये।
हल:
सन्दूक की लम्बाई = 3 मी., चौड़ाई = 2 मी., ऊँचाई = 1.80 मी.
सन्दूक का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2[ल. × चौ. + चौ. ×ऊँ. + ऊँ. ×ल.]
= 2[3 × 2 + 2× 1.80 + 1.80 × 3]
= 2[6 + 3.60 + 5.40]
= 2[6 + 9] = 2[15]
= 30 वर्ग मीटर
30 मीटर’ पर वार्निश कराने का व्यय = ₹ 30 × 12 = 360 उत्तर ।
प्रश्न 10.
यदि एक बेलन का आयतन 448π घन सेमी. और ऊँचाई 7 सेमी. (RBSESolutions.com) है तो बेलन का पाश्र्व पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
बेलन का आयतन = πr2h
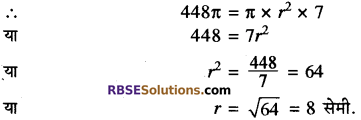
बेलन का पार्श्व पृष्ठीय क्षेत्रफल
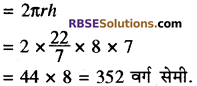
बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल
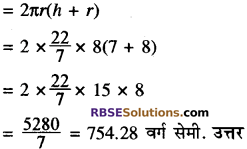
प्रश्न 11.
पानी से भरी हुई एक अर्धगोलाकार टंकी को एक पाइप द्वारा 5 लीटर प्रति सेकंड की दर से खाली किया जाता है। (RBSESolutions.com) यदि टंकी का व्यास 3.5 मी. है, तो वह कितने समय में आधी खाली हो जाएगी?

∴ 5 लीटर पानी खाली होने का समय = 1 सेकण्ड
∴ 1 लीटर पानी खाली होने का समय = \(=\frac{1}{5}\) सेकण्ड
∴ \(\frac{110 \times 1225}{24}\) लीटर पानी खाली होने का समय

अर्थात् वह टंकी 18.7 मिनट में आधी खाली हो जाएगी। उत्तर
![]()
प्रश्न 12.
1 सेमी त्रिज्या और 2 सेमी लम्बी तांबे की एक छड़ को एक (RBSESolutions.com) समान चौड़ाई वाले 18 मीटर लम्बे एक तार के रूप में बदला जाता है। तार की मोटाई ज्ञात कीजिए।
हल:
छड़ का आयतन = π × (1)2 × 2 cm.3 = 2π cm.3
समान आयतन वाले तार की लम्बाई = 18 m. = 1800 cm.
यदि तार के अनुप्रस्थ काट की त्रिज्या r है तो तार का आयतन
= π × r2 × 1800 cm.2
अतः π × r2 × 1800 = 2π [∵ दोनों का आयतन बराबर होगा।]

अतः तार के अनुप्रस्थ काट का व्यास अर्थात् मोटाई \(=2 \times \frac{1}{30} \mathrm{cm}\)
\(=\frac{1}{15} \mathrm{cm}\). उत्तर
प्रश्न 13.
42 सेमी. कोर के घन से बड़े से बड़ा लम्बवृत्तीय शंकु काटा जाता है। (RBSESolutions.com) शंकु का आयतन ज्ञात कीजिए।
(माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18)
हल:
42 सेमी. भुजा वाले घन से बड़े से बड़ा लम्बवृत्तीय शंकु काटकर निकालने के लिए उसके आधार की त्रिज्या होगी
![]()
अर्थात् त्रिज्या r = 21 सेमी.
और शंकु की ऊँचाई = भुजा = 42 सेमी.
अर्थात् h = 42 सेमी.
अतः शंकु का अभीष्ट आयतन
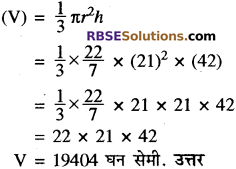
प्रश्न 14.
दो लम्बवृत्तीय बेलनों की आधार त्रिज्याओं के अनुपात 1: 2 है। (RBSESolutions.com) यदि उनके आयतनों का अनुपात 5 : 12 हो, तो उनकी ऊँचाइयों का अनुपात ज्ञात कीजिये।


निबन्धात्मक प्रश्न
प्रश्न 1.
विमाओं 5.5 cm. × 10 cm. × 3.5 cm. वाला एक घनाभ (RBSESolutions.com) बनाने के लिए 1.75 cm. व्यास और 2 mm मोटाई वाले कितने चाँदी के. सिक्कों को पिघलाना पड़ेगा?
हल:
प्रश्नानुसार, चाँदी का सिक्का बेलन के आकार का है।
चाँदी के सिक्के का व्यास = 1.75 cm.
∴ चाँदी के सिक्के की त्रिज्या \((r)=\frac{1.75}{2} \mathrm{cm}\)
चाँदी के सिक्के की मोटाई
बेलन की ऊँचाई (H) = 2 mm
अर्थात् \(h=\frac{2}{10} \mathrm{cm}\).
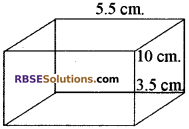
घनाभ की लम्बाई (L) = 5.5 cm.
घनाभ की चौड़ाई (B) = 10 cm.
घनाभ की ऊँचाई (H) = 3.5 cm.
![]()
माना कि चाँदी के n सिक्कों को पिघला कर नया घनाभ बनाया गया है। घनाभ का आयतन = n [चाँदी के एक सिक्के का आयतन]
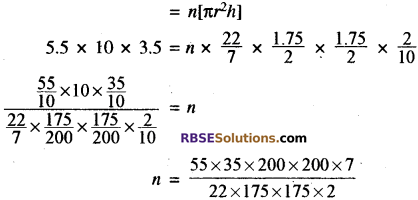
n = 400
इस प्रकार बने सिक्कों की संख्या = 400 उत्तर
![]()
प्रश्न 2.
एक कलमदानं घनाभ के आकार की एक लकड़ी से बना है (RBSESolutions.com) जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की। विमाएँ 15 cm. × 10 cm. × 3.5 cm. हैं। प्रत्येक गड्ढे की त्रिज्या 0.5 cm. है और गहराई 1.4 cm. है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए ( देखिए आकृति)।
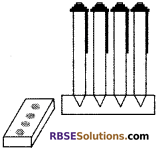
हल:
प्रश्नानुसार, घनाभ की लम्बाई (L) = 15 cm.
घनाभ की चौड़ाई (B) = 10 cm.
घनाभ की ऊँचाई (H) = 3.5 cm.
शंक्वाकार गड्ढे की त्रिज्या (r) = 0.5 cm.
शंक्वाकार गड्ढे की ऊँचाई (h) = 1.4 cm.
कलमदान में लकड़ी का आयतन
= घनाभ का आयतन – 4 [शंकु का आयतन]
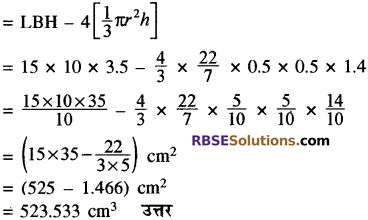
प्रश्न 3.
एक बिना ढक्कन का संदूक 2.5 सेमी. मोटी लकड़ी का बना हुआ है। (RBSESolutions.com) उसकी भीतरी लम्बाई, चौड़ाई और ऊँचाई क्रमशः 145 सेमी., 95 सेमी. व 40 सेमी. है। सन्दूक के बाहर की ओर पेन्ट कराने का व्यय ज्ञात कीजिए, यदि पेन्ट कराने की दर 4 रु. प्रति 1000 वर्ग सेमी. हो।
हल:
संदूक की बाहरी लम्बाई
= 145 + 2 × 2.5
= 145 + 5 = 150 सेमी.
संदूक की बाहरी चौड़ाई
= 95 + 2 × 2.5
= 95 + 5 = 100 सेमी.
संदूक की बाहरी ऊँचाई
= 40 + 2.5
= 42.5 सेमी.
संदूक का बाहरी क्षेत्रफल जिस पर पेन्ट होता है।

प्रश्न 4.
यदि एक समकोणिक समान्तर षट्फलक की लम्बाई, (RBSESolutions.com) चौड़ाई और ऊँचाई का अनुपात 6 : 5 : 4 है और उसका सम्पूर्ण पृष्ठीय क्षेत्रफल 33300 वर्ग सेमी. है, तो समकोणिक समान्तर घट्फलक का आयतन ज्ञात कीजिए।
हल:
माना घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 6x, 5x और 4x है।
इसका सम्पूर्ण पृष्ठीय क्षेत्रफल होगा


प्रश्न 5.
एक बेलन के आधार का क्षेत्रफल 154 वर्ग सेमी. तथा ऊँचाई 21 सेमी. है। (RBSESolutions.com) बेलन का आयतन और वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हल:
बेलन के आधार का क्षेत्रफल = 154 वर्ग सेमी.
बेलन की ऊँचाई (h) = 21 सेमी.
बेलन का आयतन = आधार का क्षेत्रफल × ऊँचाई
= 154 × 21
= 3234 घन सेमी. उतर
अतः आधार का क्षेत्रफल = πr2
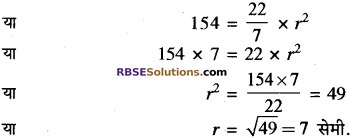
बेलन का वक्र पृष्ठीय क्षेत्रफल
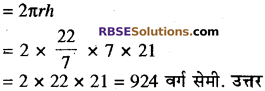
![]()
प्रश्न 6.
एक बेलन की ऊँचाई 11 सेमी. तथा उसका वक्र पृष्ठ 968 सेमी. है। (RBSESolutions.com) बेलन की त्रिज्या ज्ञात कीजिये।
हल:
बेलन की ऊँचाई h = 11 सेमी.
माना कि बेलन की त्रिज्या = r
बेलन का वक्र पृष्ठ = 2πrh = 968
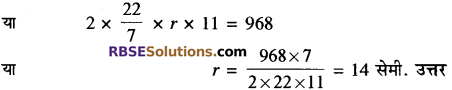
प्रश्न 7.
एक खोखले बेलन की ऊँचाई 21 डेसी मीटर है तथा इसके बाह्य व्यास व अन्तः व्यास क्रमशः 10 सेमी. व 6 सेमी. है। बेलन का आयतन ज्ञात कीजिए।
हल:
खोखले बेलन की ऊँचाई = 21 डेसी मीटर
[∵ 10 सेमी. = 1 डेसी मीटर]
= 21 × 10 = 210 सेमी.
खोखले बेलन को बाह्य व्यास = 10 सेमी.
![]()
व्यास 10 अतः बाह्य त्रिज्या
खोखले बेलन का अन्तः व्यास = 6 सेमी.
अन्त: त्रिज्या \(\left(r_{2}\right)=\frac{6}{2}=3\) सेमी.
खोखले बेलन का आयतन
\(\begin{array}{l}{=\pi\left(r_{1}^{2}-r_{2}^{2}\right) h} \\ {=\frac{22}{7}\left[(5)^{2}-(3)^{2}\right] \times 210}\end{array}\)
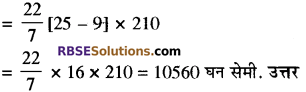
प्रश्न 8.
एक बेलन की त्रिज्या और ऊँचाई का अनुपात 1: 3 है। (RBSESolutions.com) यदि बेलन का आयतन 3234 सेमी. है तो बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिये।
हल:
माना बेलन की त्रिज्या r तथा ऊँचाई 3r है।

अतः बेलन की ऊँचाई h = 3 × 7 = 21 सेमी.
बेलन का सम्पूर्ण पृष्ठीय क्षेत्रफल
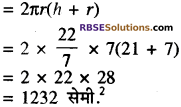
प्रश्न 9.
एक रोलर की लम्बाई 2 मी. और व्यास 1.4 मी. है। ज्ञात कीजिए 5 चक्कर लगाने (RBSESolutions.com) में रोलर कितना क्षेत्र समेतले करेगा?
हल:
रोलर की लम्बाई (h) = 2 मीटर
रोलर का व्यास = 1.4 मीटर
रोलर की त्रिज्या \(=\frac{1.4}{2}=0.7\) मीटर
रोलर के 1 चक्कर लगाने में समतल किया क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल
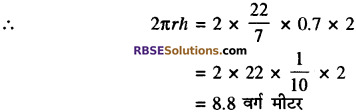
∴ 5 चक्कर लगाने में समतल किया क्षेत्रफल = 8.8 ×5 = 44 वर्ग मीटर
प्रश्न 10.
एक शंकु के आधार का व्यास 12 मीटर और तिर्यक ऊँचाई 10 मीटर है। (RBSESolutions.com) शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिये।
हल:
दिया है:
शंकु के आधार का व्यास = 12 मीटर
![]()
और शंकु की तिर्यक ऊँचाई (l) = 10 मीटर
शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल
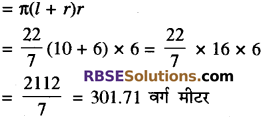
अतः शंकु का सम्पूर्ण पृष्ठीय क्षेत्रफल = 301.71 वर्ग मीटर है। उत्तर
![]()
प्रश्न 11.
यदि एक शंकु का वक्र पृष्ठ 2035 वर्ग सेमी. और (RBSESolutions.com) आधार का व्यास 35 cm हो तो शंकु की तिर्यक ऊँचाई ज्ञात कीजिये।
हल:
दिया है:
शंकु का वक्र पृष्ठ = πrl = 3035 cm2

अत: शंकु की तिर्यक ऊंचाई (l) = 37 सेमि. होगी। उतर
प्रश्न 12.
एक शंकु का आयतन 16632 घन सेमी. है और ऊँचाई 9 सेमी. है। (RBSESolutions.com) इसके आधार की त्रिज्या ज्ञात कीजिये।
हल:
दिया है:
शंकु का आयतन = 16632 घन सेमी.
शंकु की ऊँचाई (h) = 9 सेमी.

![]()
अतः शंकु की त्रिज्या = 42 सेमी. उत्तर
प्रश्न 13.
किसी शंकु की त्रिज्या और ऊँचाई का अनुपात 5 : 12 और आयतन 2512 घन सेमी. (RBSESolutions.com) है तो शंकु की तिर्यक ऊँचाई और आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 लीजिए)
हल:
शंकु की त्रिज्या और ऊँचाई का अनुपात = 5: 12
शंकु की त्रिज्या (r) = 5x सेमी.
शंकु की ऊँचाई (h) = 12x सेमी.
शंकु को आयतन = 2512 घने सेमी.
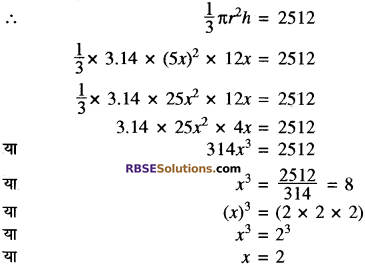
अतः शंकु की त्रिज्या = 5 × 2 = 10 सेमी.
शंकु की ऊँचाई = 12 × 2 = 24 सेमी. उत्तर
प्रश्न 14.
एक शंकु के आकार के टेन्ट की ऊँचाई 14 मीटर है तथा आधार का क्षेत्रफल 346.5 मीटर है। (RBSESolutions.com) यह टेन्ट 1.5 मीटर चौड़े केनवास से बना हुआ है तो कैनवास की लम्बाई ज्ञात कीजिए।
हल:
शंकु के आकार के टेन्ट की ऊँचाई h = 14 मीटर
त्रिज्या = r मीटर
शंकु के आधार का क्षेत्रफल = πr2
आधार का क्षेत्रफल = 346.5 मीटर2
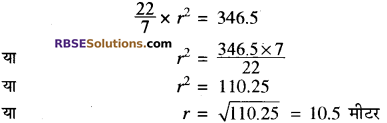
टेन्ट की तिरछी लम्बाई
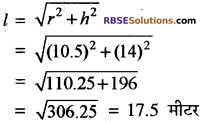
केनवास को क्षेत्रफल = टेन्ट के तिर्यक पृष्ठ का क्षेत्रफल
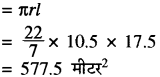
केनवास की लम्बाई
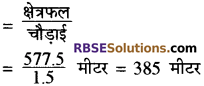
![]()
प्रश्न 15.
एक शंकु की ऊँचाई 24 सेमी. तथा वक्र पृष्ठीय क्षेत्रफल 550 वर्ग सेमी., (RBSESolutions.com) शंकु की त्रिज्या ज्ञात कीजिये।
हल:
माना शंकु की त्रिज्या r तथा तिर्यक ऊँचाई l है, तो
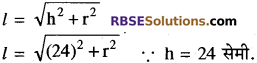
शंकु का वक्र पृष्ठीय क्षेत्रफल = 550 वर्ग सेमी.
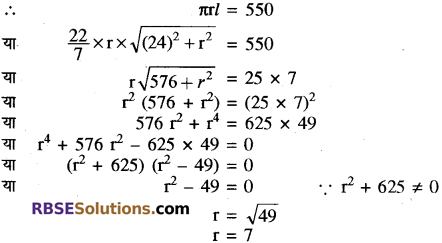
शंकु की त्रिज्या = 7 सेमी. उत्तर
प्रश्न 16.
14 सेमी. व्यास वाले एक अर्द्धगोलीय ठोस में से बड़ा से बड़ा लंब वृत्तीय शंकु निकाला गया है। (RBSESolutions.com) शेष.ठोस का आयतन ज्ञात कीजिए।
हल:
यहाँ अर्द्धगोलीय ठोस का आयतन
\(=\frac{2}{3} \pi \mathrm{r}^{3}\)

प्रश्न 17.
14 सेमी. की भुजा वाले घन से एक बड़ा से बड़ा गोला काटकर निकाला गया है। (RBSESolutions.com) इस गोले का संपूर्ण पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।
हल:
14 सेमी. भुजा वाले घन से बड़े से बड़ा गोला काटकर निकालने के लिए उसकी त्रिज्या होगी
![]()
7 सेमी. त्रिज्या वाले गोले का संपूर्ण पृष्ठीय क्षेत्रफल होगा
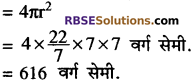
7 सेमी. त्रिज्या वाले गोले का आयतन होगा \(=\frac{4}{3} \pi r^{3}\)

अतः सम्पूर्ण पृष्ठीय क्षेत्रफल = 616 सेमी.2 और आयतन = 1437.33 सेमी.3 उत्तर
प्रश्न 18.
7 सेमी. व्यास वाला एक गोली पानी से आंशिक भरे एक बेलनाकार बर्तन में डाला जाता है। (RBSESolutions.com) बर्तन के आधार का व्यास 14 सेमी. है। यदि गोला पूर्णतया पानी में डूबा हो, तो पानी का स्तर कितना ऊपर उठ जायेगा?
हल:
गोले को व्यास = 7 सेमी.

पुनः बेलनाकार बर्तन के आधार का व्यास = 14 सेमी.
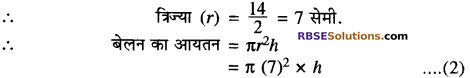
समीकरण (1) तथा (2) को बराबर करने पर
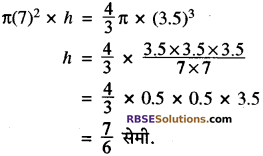
अतः गोला डालने पर पानी का स्तर \(\frac{7}{6}\) सेमी. ऊपर उठ जायेगा। उत्तर
![]()
प्रश्न 19.
दो गोलों के पृष्ठीय क्षेत्रफलों का अनुपात 9: 16 है। (RBSESolutions.com) उनके आयतनों का अनुपात ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18)
हल:
पहले गोले का पृष्ठीय क्षेत्रफल \(\mathrm{S}_{1}=4 \pi r_{1}^{2}\)
यहाँ पर r1 पहले गोले की त्रिज्या है।
इसी तरफ से दूसरे गोले का पृष्ठीय क्षेत्रफल
\(\mathrm{S}_{2}=4 \pi r_{2}^{2}\)
यहाँ पर r2 दूसरे गोले की त्रिज्या है।
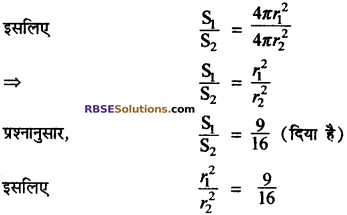
![]()
पहले गोले का आयतन \(\mathbf{V}_{1}=\frac{4}{3} \pi r_{1}^{3}\)
इसी तरह से दूसरे गोले का आयतन

प्रश्न 20.
एक रोलर की लम्बाई 2.5 मीटर और व्यास 1.4 मीटर है। 10 चक्कर लगाने में रोलर (RBSESolutions.com) कितना क्षेत्र समतल करेगा? (माध्य. शिक्षा बोर्ड, 2018)
हल:
दिया गया है:
रोलर की लम्बाई = 2.5 मीटर, अर्थात् रोलर की ऊँचाई = 2.5 मीटर
रोलर का व्यास = 1.4 मीटर
∴ h = 2.5 मीटर
रोलर का एक चक्कर में क्षेत्रफल = रोलर का वक्र पृष्ठीय क्षेत्रफल

अतः 10.चक्कर लगाने में क्षेत्रफल
![]()
![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 16 पृष्ठीय क्षेत्रफल एवं आयतन Additional Questions, drop a comment below and we will get back to you at the earliest.