RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.1 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | Surface Area and Volume |
| Exercise | Exercise 16.1 |
| Number of Questions Solved | 12 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.1
Ex 16.1 Class 10 RBSE Question 1.
The height, breadth and length of an (RBSESolutions.com) cuboid are 5 cm, 9 cm and 12 cm respectively. Find the total surface area and the volume of cuboid.
Solution :
Given
Length of cuboid (l) = 12 cm
Breadth (b) =9 cm
and Height (h) = 5 cm
Total surface area of cuboid = 2(lb + bh + hl)
= 2[(12 × 9) + (9 × 5) +(5 × 12)]
= 2[108 + 45 + 60]
2 × 213 = 426 cm2
Volume = l × b × h
= 12 × 9 × 5 = 540 cm3
Hence, total surface area of cuboid 426 cm2
And volume of the cuboid 540 cm3
RBSE Solutions For Class 10 Maths Chapter 16 Question 2.
The cores of three cubes are 8 cm, 6 cm and 1 cm (RBSESolutions.com) respectively. Having melted these cubes a new cube is recastesd. Find the total surface area of the new cube recanted.
Solution :
Volume of the cube with core of 8 cm = (core)3
= 83 = 512 cm3
Volume of the cube with core 6 cm = (core)3
= (6)3 = 216 cm3.
Volume of the cube with core 1 cm = (core)3
= (1)3 = 1 cm3.
The total volume of three cubes 512 + 216 + 1 = 729 cm3.
Having melted these cubes, a new cube is recasted
∴ The volume of the cube recasted = 729 cm3
⇒ (core)3 = 729
⇒ core = \(\sqrt [ 3 ]{ 729 } \)
= (93)1/3 = 9 cm
Total surface area of cuboid recasted =6 (core)2
6 × 9 × 9 = 486 cm2.
Hence the surface area of the new cube = 486 cm2.
RBSE Solutions For Class 10 Maths Chapter 16.1 Question 3.
The measures of a box are 50 cm × 36 cm × 25 cm. To make (RBSESolutions.com) the cover of the box. How much cloth is needed?
Solution :
Given
Length of box (l) = 50 cm
Breadth of box (b) = 36 cm
Height of box (h) = 25 cm
The necessary cloth to make its cover = surface area of the box
= 2(lb + bh + hl)
= 2[(50 × 36) + (36 + 25) + (25 + 50)]
= 2[1800 + 900 + 1250]
= 2 × 3950 = 7900 cm2.
Class 10 Maths RBSE Solution Chapter 16 Question 4.
Each of the face of cube is 100 sq. cm. If the cube Is cut of (RBSESolutions.com) parallel to its base and divided into two equal parts. Find the total surface area of each part separately.
Solution :
Given
The area of each face of cube = 100 cm2
∴ core of the cube = \(\sqrt { 100 } \) = 10 cm
When a cube is cut of parallel to its base and divided into two equal parts, then two cuboids are formed.
In which the length of each cube (l) = 10 cm
Breadth (b) = 5 cm
Height (h) = 10 cm
∴ And the surface area of each cuboid formed
= 2(lb + bh + hl)
= 2[(10 × 5) + (5 × 10) + (10 × 10)]
= 2[50 + 50 + 100]
= 2 × 200=400 cm2
Hence, the surface area of each cuboid formed = 400 cm2.
Exercise 16.1 Class 10 RBSE Question 5.
A box with out upper lid is made of wood of width 3 cm. Its external (RBSESolutions.com) length, breadth and height are 146 cm, 116 cm and 83 cm respectively.
Find cost of painting inside if the rate of painting = ₹ 2 per 1000 sq.cm.
Solution : Given
The external length of box = 146 cm
breadth = 116 cm
height = 83 cm
The width of the wood = 3 cm

∴ The internal (RBSESolutions.com) length of box = (146 – 3 – 3) = 140 cm.
Internal breadth of box = (116 – 3 – 3) = 110 cm
Internal height of box = 83 – 3 = 80 cm.
Besides of the lid, the internal total surface area of the box
= 2(l + b) × h + l × b
= 2(140 + 110) × 80 + (140 × 110)
= 160 × 250 + 15400
= 55400 sq. cm.
The cost of painting of 1000 sq. cm. = ₹ 2.
∴ The cost of painting of 55400 = \(\frac { 2\times 55400 }{ 1000 } \) = ₹ 110.80
Hence the cost of painting the box = ₹ 110.80.
RBSE Class 10 Maths Chapter 16 Question 6.
The sum of the length, breadth and height of a (RBSESolutions.com) cuboid is 19 cm and the length of its diagonal is 11 cm. Find the total surface area of the cuboid.
Solution :
Given, the sum of the length, breadth and height of cuboid = 19 cm.
And the length of its diagonal = 11 cm.
Let the length, breadth and height of the cuboid be l, b and h respectively.
∴ l + b + h = 19 cm …(i)
and \(\sqrt { { l }^{ 2 }+{ b }^{ 2 }+{ h }^{ 2 } } \) = 11 cm. …(ii)
Squarnng both (RBSESolutions.com) the sides, we get
l2 + b2 + h2 = (11)2 = 121 …(iii)
We know that,
(l + b + h)2 =[l2 + b2 + h2] + 2(lb + bh + hl)
⇒ (19)2 = 121 + 2(lb + bh + hl)
⇒ 361 = 121 + 2(lb + bh + hl)
⇒ 2(lb + bh + hl) = 361 – 121
⇒ 2(lb + bh + hl) = 240 sq. cm.
Hence, the total surface area of cuboid = 240 cm2.
Ch 16 Maths Class 10 RBSE Question 7.
A room contains 180 m3 air in it. Find the (RBSESolutions.com) height of the room if its floor is a square with side 6 meter.
Solution :
Let the height of the room be h meter.
Since the floor of the room is square shaped.
∴ the length of room (l) = 6 m
also the breadth of room (b) = 6 m
The volume of the room = 180 m3
⇒ l × b × h = 180
6 × 6 × h = 180
h = \(\frac { 180 }{ 6\times 6 }\) = 5 m.
Hence the height of the room = 5 m.
Chapter 16 Maths Class 10 RBSE Question 8.
How many brisks are need to build a wall of (RBSESolutions.com) length 44 meter, height 1.5 meter and broad 85 cm. The measurement of each brick is 20 cm × 10 cm × 17 cm.
Solution :
Length of the wall = 44 meter
=44 × 100 cm = 4400 cm
height = 1.5 meter = 1.5 × 100 = 150 cm
width of the wall = 85 cm
volume of (RBSESolutions.com) the wall = length × breadth × height
=4400 × 85 × 150 cm3.
length of one brick = 22 cm
breadth = 10 cm
height = 17 cm
The volume of a brick 22 × 10 × 17 cm3.

Hence, 15000 bricks will be needed.
16.1 Class 10 Question 9.
Find the length of the longest rod can be put (RBSESolutions.com) in a room with dimensions 10 meter, 8 meter and 6 meter.
Solution :
Given
The length of the room (l) = 10 meter
breath (b) = 8 meter
height (h) = 6 meter
The longest rod that can be put in the room will be equal of its diagonal.
∴ Diagonal = \(\sqrt { { l }^{ 2 }+{ b }^{ 2 }+{ h }^{ 2 } } \)
= \(\sqrt { { 10 }^{ 2 }+{ 8 }^{ 2 }+{ 6 }^{ 2 } } \)
= \(\sqrt { 200 } \)
= 10√2 m
∴ The length of the longest rod = 10√2 m.
Class 10 Maths Chapter 16 RBSE Question 10.
The volume of a (RBSESolutions.com) cube ¡s 512 m3. Find its side.
Solution :
Given:
The volume of cube = 512 cm3.
⇒ (side)3 = 512
side = \(\sqrt [ 3 ]{ 512 } \)
side = (8 × 8 × 8)1/3
= (83)1/3 = 8 m.
Hence side of the cube = 8 m
RBSE Class 10 Maths Chapter 16.1 Question 11.
The length, breath and height of a wall are 5 m, 30 cm and 3 m. How (RBSESolutions.com) many bricks will be needed to build of the wall. The dimensions of one brick are 20 cm × 10 cm × 7.5 cm.
Solution :
Given
The length of wall = 5 m
= 5 × 100 = 500 cm
breadth = 30 cm
height = 3 m
= 3 × 1000 = 300 cm3
The volume of the (RBSESolutions.com) wall = length × breadth × height
= 500 × 30 × 300 cm3.
For a brick = 20 cm
breadth = 10 cm
and height = 7.5 cm
Volume of one brick = l × b × h
= 20 × 10 × 7.5 cm3
∴ Number of bricks needed
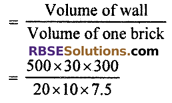
= 3000
Hence, 3000 bricks are needed.
RBSE Solution Class 10 Maths Chapter 16 Question 12.
The ratio of the length, breadth and height (RBSESolutions.com) of a cuboid is 5 : 3 : 2. If the total surface area of the cuboid in 558 cm2. Find the length of its sides.
Solution :
Let for the cuboid,
length = 5x
breadth = 3x
and height = 2x
Total surface area of cuboid = 558 cm2
⇒ 2(lb + bh + hl) = 558
⇒ (5x × 3x) + (3x × 2x) + (2x × 5x) = \(\frac { 558 }{ 2 }\)
⇒ 15x2 + 6x2 + 10x2 = 279
31x2 = 279
x2 = \(\frac { 279 }{ 31 }\)
x2 = 9
x = √9
= 3 cm
∴ The length of the (RBSESolutions.com) cuboid 5 × 3 = 15 cm
breadth = 3 × 3 = 9 cm
height = 2 × 3 = 6 cm
Hence, the length = 15 cm, breadth = 9 cm and height = 6 cm.
We hope the given RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.1 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.1, drop a comment below and we will get back to you at the earliest.