RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | Surface Area and Volume |
| Exercise | Exercise 16.2 |
| Number of Questions Solved | 13 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.2
ex 16.2 class 10 rbse Question 1.
The diameter and height of a cylinder are 14 cm and 15 cm respectively. Find (RBSESolutions.com) the total surface area and volume of the cylinder.
Solution :
Given,
Diameter of cylinder = 14 cm
∴ Radius of cylinder (r) = \(\frac { 14 }{ 21 }\) = 7 cm
The height of cylinder (h) = 15 cm
Total surface area of cylinder = 2πr(h + r)
2 × \(\frac { 22 }{ 7 }\) × 7(15 + 7)
= 2 × 22 × 22
= 968 cm2
Volume of cylinder = πr2h
= \(\frac { 22 }{ 7 }\) × (7)2 × 15
= \(\frac { 22\times 7\times 7\times 15 }{ 7 } \)
= 2310 cm3.
Hence, Total surface area of cylinder is 968 cm2 and Volume is 2310 cm3.
rbse solutions for class 10 maths chapter 16.2 Question 2.
The height of a right circular cylinder is 7 cm and radius is 3 cm. Find its (RBSESolutions.com) curved surface area, total surface area and volume.
Solution :
Given :
Height of cylinder (h) = 7 cm
Radius of base (r) = 3 cm
Curved surface area of cylinder = 2πrh
= 2 × \(\frac { 7 }{ 5 }\) × 3 × 7
= 22 × 6
= 132 cm2.
Total surface area of cylinder = 2πr(h + r)
= 2 × \(\frac { 22 }{ 7 }\) × 3(7 + 3)
2 × \(\frac { 22 }{ 7 }\) × 3 × 10
= \(\frac { 1320 }{ 7 }\)
= 188.57 cm2
Volume of cylinder = πr2h
= \(\frac { 22 }{ 7 }\) × 3 × 3 × 7
= 22 × 3 × 3
= 198 cm3
Hence, curved surface area of cylinder = 132 cm2.
Total surface area = 188.57 cm2 and Volume = 198 cm3.
exercise 16.2 class 10 rbse Question 3.
The area of one end of a cylinder is 154 cm2 and its height is 21 cm. Find (RBSESolutions.com) the volume and curved surface area of cylinder.
Solution:
Given
Height of cylinder (h) = 21 cm
Area of its one end = 154 cm2
πr2 = 154
⇒ \(\frac { 22 }{ 7 }\) × r2 = 154
r2 = \(\frac { 154\times 7 }{ 22 } \)
= \(\frac { 1078 }{ 22 }\) = 49
r = √49 = \(\sqrt { 7\times 7 }\)
r = 7 cm
Volume of cylinder = πr2h
= \(\frac { 22 }{ 7 }\) × 7 × 7 × 21
= 22 × 7 × 21
= 3234 cm3
Curved surface area = 2πrh
= 2 × \(\frac { 22 }{ 7 }\) × 7 × 21
= 2 × 22 × 21
= 924 cm2.
Hence, the volume of cylinder= 3234 cm3
curve surface area = 924 cm2
rbse class 10 maths chapter 16.2 Question 4.
The ratio of radii of two right circular cylinder is 2 : 3 and the ratio of (RBSESolutions.com) their heights is 5 : 4. Find the ratio of their curved surface areas and volume.
Solution :
Let the radius of first cylinder be r1 and height be h1 and let the radius of second cylinder be r2 and height be h2. Then according to question
\(\frac { { r }_{ 1 } }{ { r }_{ 2 } } \) = \(\frac { 2 }{ 3 }\)
and \(\frac { { h }_{ 1 } }{ { h }_{ 2 } } \) = \(\frac { 5 }{ 4 }\)
Curved surface area of first cylinder S1 = 2πr1h1
and curved surface area of second cylinder S2 = 2πr2h2

Hence, ratio of curved surface area = 5 : 6
and ratio of volumes = 5 : 9
class 10 maths rbse solution chapter 16.2 Question 5.
The total surface area of a solid cylinder is 462 cm2. Its curved surface (RBSESolutions.com) area is one third of its total surface area. Find the volume of the cylinder.
Solution :
Let radius of cylinder be r and height be h. Then
Given, Total surface area = 262 cm2.
⇒ 2πr(h+r) = 264
According to question.
Curved surface area
= \(\frac { 1 }{ 3 }\) (total surface area)
= \(\frac { 1 }{ 3 }\) × 462
= 2πrh = 154 …(ii)
on dividing equation (i) by equation (ii) we get.

Hence the volume of cylinder = 539 cm3
class 10 maths rbse solution chapter 16 exercise 16.2 Question 6.
The curved surface area and height of (RBSESolutions.com) cylinder are 660 cm2 and 15 cm respectively. Find its volume.
Solution :
Let radius of cylinder be r.
Given, height of cylinder = 15cm
and curved surface area = 660 cm2
⇒ 2πrh = 660
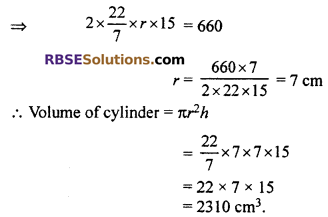
Hence, the volume of cylinder = 2310 cm3.
ex 16.2 class 10 Question 7.
Volume of a cylinder is 30π cm3 and the base is 6π cm2. Find the (RBSESolutions.com) height of the cylinder.
Solution :
Given,
Volume of cylinder =30π cm3
and base area = 6π cm2
:. Volume of cylinder = base area × height
⇒ 30π = 6π × height
⇒ height = \(\frac { 30\pi }{ 6\pi } \)
= 5 cm.
Hence, the height of the cylinder 5 cm.
rbse solutions for class 10 maths chapter 16 Question 8.
Volume and curved surface area of a cylinder are 1650 cm3 and 660 cm2 respectively. (RBSESolutions.com) Find the radius and height of the cylinder.
Solution :
Let radius of cylinder be r. and height be h.
Given volume of cylinder 1650 cm3
⇒ πr2h = 1650 ….(i)
Curved surface area of cylinder = 660 cm2
⇒ 2πrh = 660 …(ii)
On dividing (i) by (ii), we get
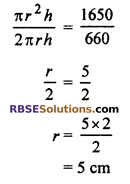
substituting this value of r in equation (ii), we get
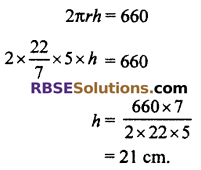
Hence, the radius is 5 cm and height is 21 cm.
class 10 maths rbse solution chapter 16 Question 9.
The height and the radius of a cylinder are 7.5 cm and 3.5 cm respectively. Find the (RBSESolutions.com) ratio of its total surface area and curved surface area.
Solution :
Given,
Height of cylinder (h) = 7.5 cm
Radius (r) = 3.5 cm
Total surface area = 2πr(h + r)

Hence, required ratio = 22 : 15
chapter 16 maths class 10 rbse Question 10.
A well 20 m deep and 7 m ¡n diameter is dug. The earth taken out is spread to form a 22 m × 14 m embankment. Find the height of the embankment.
Solution :
Given,
Diameter of well = 7 m
∴ Radius of well (r) = \(\frac { 7 }{ 2 }\) m
Depth of well (h) = 20m
The volume of the soil taken out from well = πr2h
= \(\frac { 22 }{ 7 }\) × \({ \left( \frac { 7 }{ 2 } \right) }^{ 2 }\) × 20
= 770 cm3.
The length of plateform (L) = 22 m
The breadth of plateform (B) = 14 m
Let the height of plateform be H.
Volume of plateform = L x B x H m3.
= 22 × 14 × H m3
According to question
Volume of plateform = volume of earth digut 22 × 14 × H = 770
H = \(\frac { 770 }{ 22\times 14 }\)
= 2.5 m.
Hence the height of plate form is 2.5 m.
rbse class 10 maths chapter 16 Question 11.
In a cylindrical vessel 30800 cm3 water can be filled. If the internal radius of vessel is 14 cm. Find it curved surface area.
Solution :
Given
The internal radius of vessel r = 14 cm
Volume of the vessel 30800 cm3
Let the height of the vessel be h.
∴ πr2h = 30800 cm3.
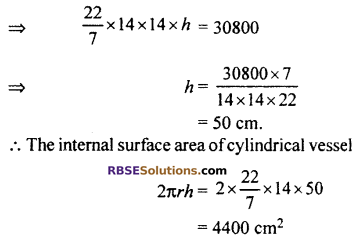
Hence the internal curved surface area of cylindrical vessel = 4400 cm2
class 10 maths chapter 16.2 Question 12.
If the width of a hollow cylinder is 2 cm. Its internal diameter is 14 cm and height 26 cm. The two ends of cylinder are opened. Find the total surface area of the hollow cylinder.
Solution :
Given internal diameter of hollow cylinder =14 cm.
∴ Internal radius (r2) = 7 cm
Width of the cylinder = 2 cm
∴ External radius (r1) = 7 + 2 = 9 cm
Height (h) 26 cm.
Total surface area of cylinder
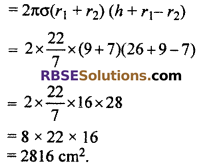
Hence, the total surface area of cylinder = 2816 cm2
ch 16 maths class 10 rbse Question 13.
A hollow cylinder ¡s open at both ends. Its height 20 cm and internal and external diameters arc 26 cm and 30 cm respectively. Find the volume of the metal by which cylinder is made of.
Solution :
Given,
Height of the cylinder(h) = 20 cm
Internal diameter = 26 cm
Internal radius (r1) = \(\frac { 26 }{ 2 }\) = 13 cm
External diameter = 30 cm
External radius (r2) = \(\frac { 30 }{ 2 }\) = 15 cm
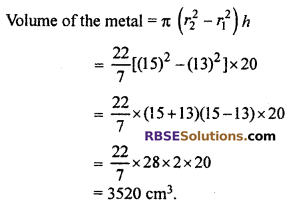
Hence, the volume of the metal = 3520 cm3
We hope the given RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.2, drop a comment below and we will get back to you at the earliest.