RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.4 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.4.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 16 |
| Chapter Name | Surface Area and Volume |
| Exercise | Exercise 16.4 |
| Number of Questions Solved | 14 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.4
Ex 16.4 Class 10 RBSE Question 1.
Find the surface area and the volume of a sphere (RBSESolutions.com) with radius 1.4 cm.
Solution :
Given
Radius of sphere (r) = 1.4 cm
Surface area = 4πr2
= 4 × \(\frac { 22 }{ 7 }\) × 1.4 × 1.4
= 24.64 cm2
Volume of the sphere = \(\frac { 4 }{ 3 }\)πr2
= \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 1.4 × 1.4 × 1.4
= 11.5 cm3
Hence, surface area of sphere = 24.64 cm2 and its volume = 11.5 cm3
16.4 Class 10 RBSE Question 2.
The surface area of a sphere is 616 cm2. Find (RBSESolutions.com) the volume of the sphere.
Solution :
Let radius of sphere be r.
Given, Surface area of sphere = 616 cm2
∴ 4πr2 = 616
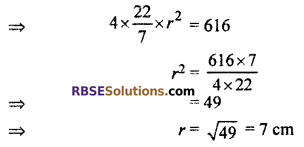
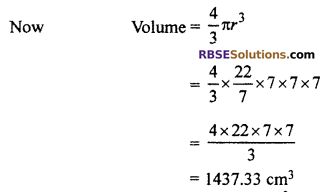
Hence, volume of sphere = 1437.33 cm3
RBSE Solutions For Class 10 Maths Chapter 16.4 Question 3.
Radius of a hemisphere is 4.5 cm. Find its total (RBSESolutions.com) surface area and volume.
Solution :
Given,
Radius of hemisphere (r) = 4.5 cm
Surface area of hemisphere = 3πr2
Let
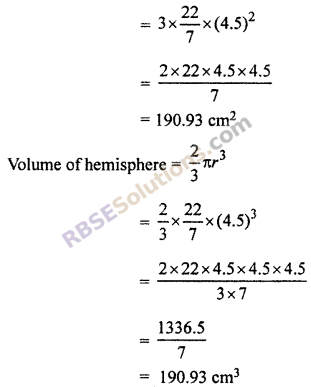
Hence, total surface area = 190.93 cm2 and volume = 190.93 cm3
Exercise 16.4 Class 10 RBSE Question 4.
The volume of a sphere is 38808 cm3. Find its (RBSESolutions.com) surface area.
Solution :
Let radius of the sphere be r,
Volume of sphere = 38808 cm3
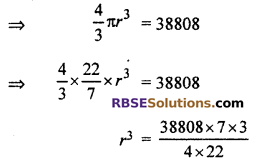
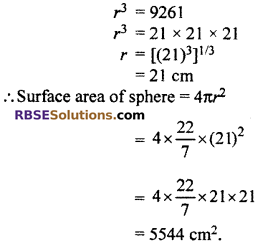
Hence, the surface area of sphere = 5544 cm2
RBSE Class 10 Maths Chapter 16.4 Question 5.
A cylinder is made of glass, whose radius and (RBSESolutions.com) height are 4 cm and 10 cm respectively. By melting it, how many sphere with radii 2 cm each can be recasted?
Solution :
Given, for a cylinder
Radius = 4 cm
And height = 10 cm
Volume = πr2h
= π × 4 × 4 × 10 cm3.
Again the radius of a sphere recasted (r) = 2 cm.
Volume of sphere = \(\frac { 4 }{ 3 }\)πr2
= \(\frac { 4 }{ 3 }\) × π × (2)3
Let the number of sphere recasted be n, then
Volume of the cylinder = n × volume of sphere
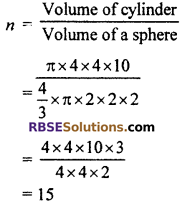
Hence, the number of sphere recasted = 15
RBSE Solutions For Class 10 Maths Chapter 16 Question 6.
The thickness of hollow spherical shell is 2 cm. If its external (RBSESolutions.com) radius is 8 cm find the volume of metal used in it.
Solution :
Given,
External radius of hollow spherical shell r1 = 8 cm.
Internal radius r2 = 8 – 2 = 6
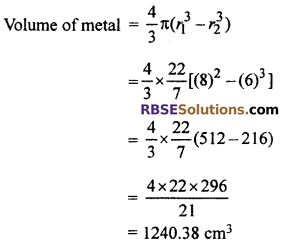
Hence, volume of the metal used = 1240.38 cm3
Chapter 16 Maths Class 10 RBSE Question 7.
How many cones with radius 3 cm and height 6 cm can be (RBSESolutions.com) formed by melting a metallic sphere with radius 9 cm.
Solution :
Given,
Radius of sphere (r) = 9 cm
Volume of the sphere = \(\frac { 4 }{ 3 }\)πr3
= \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 9 × 9 × 9 cm3
For a cone,
Radius (R) = 3 cm
Height (h) = 6 cm
Volume of the cone = \(\frac { 1 }{ 3 }\)πr2h
= \(\frac { 1 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × 3 × 3 × 6 cm3
Let the number of cones recasted be n.
∴ Volume of sphere = n × volume of a cones
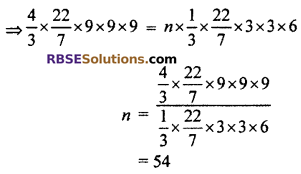
Hence, the number of cones recasted = 54.
Class 10 Maths RBSE Solution Chapter 16 Question 8.
Eight spheres of same volumes are recasted by melting a metallic (RBSESolutions.com) sphere with radius of 10 cm. Find the volume of the recasted sphere.
Solution :
Given,
Radius of the metallic sphere (r) = 10 cm
∴ Volume of sphere = \(\frac { 4 }{ 3 }\)πr3
= \(\frac { 4 }{ 3 }\) × π × r × (10)3
Let the radius of each recasted spheres be R.
∴ The volume of large sphere =8 × volume of spheres with radius R
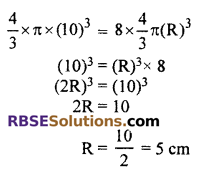
Hence, radius of the (RBSESolutions.com) sphere casted = 5 cm.
Surface area of sphere = 4πR2
= 4 × π × (5)2
=4 × π × 25
= 100π cm2
Hence, surface area of casted sphere = 100π cm2
RBSE Solutions For Class 10 Maths Chapter 16 Miscellaneous Question 9.
If surface area of a sphere ¡n 5544 cm2, then find its volume.
Solution :
Let radius of sphere be r, then
Given, surface area of sphere = 5544 cm2
4πr2 = 5544

Hence, volume of sphere = 38808 cm3
Class 10 Maths RBSE Solution Chapter 16 Question 10.
The measures of a solid cuboid are 66 cm, 42 cm and 21 cm respectively. How many (RBSESolutions.com) spheres with diameter 4.2 cm each can be recasted by melting it.
Solution :
Length (l) = 66 cm
Breadth (b) = 42 cm
and height (h) = 21 cm
Volume of cuboid = l × b × h
= 66 × 42 × 21 cm3
Diameter of sphere recasted = 4.2 cm
radius (r) = \(\frac { 4.2 }{ 2 }\) = 2.1 cm
Volume of sphere = \(\frac { 4 }{ 3 }\)π × (2.1)3
Let by melting the cuboid n spheres are formed.
∴ Volume of cuboid = n × volume of sphere
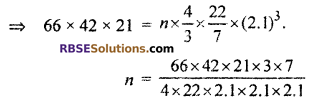
Hence, the number of sphere reformed = 1500
RBSE Class 10 Maths Chapter 16 Question 11.
A sphere with diameter 6 cm is put into the water filled in a (RBSESolutions.com) cylindrical vessel with diameter 12 cm. How much the water level in the vessel will rise?
Solution :
Given,
Diameter of sphere = 6 cm
radius (r) = \(\frac { 6 }{ 2 }\) = 3 cm
Volume of sphere = \(\frac { 4 }{ 3 }\)πr3
= \(\frac { 4 }{ 3 }\) × \(\frac { 22 }{ 7 }\) × (3)3
Diameter of cylindrical vessel = 12 cm
radius (R) = \(\frac { 12 }{ 2 }\) = 6 cm
When the sphere is put into the vessel, the water level rises by h.
∴ Volume of sphere = volume of water rise into cylinder.
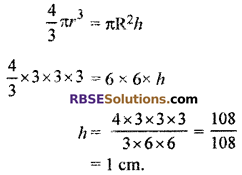
Hence, water level will rise in vessel = 1 cm.
Ch 16 Maths Class 10 RBSE Question 12.
A hemispherical bowl with internal radius 9 cm is filled with liquid (RBSESolutions.com) This liquid is to fill into the smaller cylindrical bottle with diameter 3 cm and height 4 cm. How many bottle will be needed to fill whole liquid?
Solution :
Given,
Radius of hemispherical bowl (r) = 9 cm
Volume of the bowl = \(\frac { 2 }{ 3 }\) × π × r3
= \(\frac { 2 }{ 3 }\) × π × (9)3cm3
Diameter of cylindrical bottle = 3 cm
Radius = \(\frac { 3 }{ 2 }\) cm
And height = 4 cm
Volume of the bottle = πr2h
= π\({ \left( \frac { 3 }{ 2 } \right) }^{ 2 }\) × 4
Let n bottles will be needed to be filled (RBSESolutions.com) the whole Liquid
∴ According to the question.
Volume of hemispherical bowl = n × volume of cylindrical bottles.
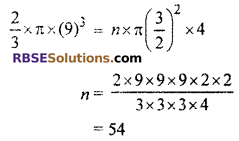
Hence, 54 bottles will be needed.
Class 10 Maths Chapter 16 RBSE Question 13.
The diameter of a sphere is 0.7 cm. From a water tank, 3000 spheres (RBSESolutions.com) completely filled with water is thrown out. Find the volume of the
water thrown out.
Solution :
Given,
Diameter of sphere = 0.7 cm
Radius (r) = \(\frac { 0.7 }{ 2 }\)cm
∴ Volume of sphere V = \(\frac { 4 }{ 3 }\)πr3
= \(\frac { 4 }{ 3 }\)π\({ \left( \frac { 0.7 }{ 2 } \right) }^{ 3 }\)cm3
Volume of water thrown out = 3000 × volume of sphere
= 3000 × \(\frac { 4 }{ 3 }\)π\({ \left( \frac { 0.7 }{ 2 } \right) }^{ 3 }\)
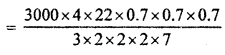
= 539 cm3
Surface Area And Volume Class 10 RBSE Question 14.
The external and internal diameters of hemispheric (RBSESolutions.com) bowl are 43 cm and 42 cm respectively. If the coloring cost is paise 7 per cm2, find the total cost of coloring the bowl.
Solution :
Given,
External diameter of hemispherical bowl = 43 cm
∴ External radius (r1) = \(\frac { 43 }{ 2 }\) cm
Internal diameter = 42 cm
∴ Internal radius (r2) = \(\frac { 42 }{ 2 }\) = 21 cm
External surface area of bowl = 2πr12
And internal (RBSESolutions.com) surface area = 2πr22
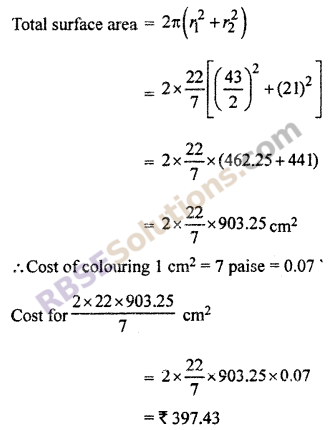
Hence, cost of (RBSESolutions.com) coloring the bowl = ₹ 397.43
We hope the given RBSE Solutions for Class 10 Maths Chapter 16 Surface Area and Volume Ex 16.4 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 16 Surface Area and Volume Exercise 16.4, drop a comment below and we will get back to you at the earliest.