RBSE Solutions for Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions

RBSE Solutions for Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 17
Chapter Name	Measures of Central Tendency
Exercise	Additional Questions
Number of Questions Solved	37
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions

Multiple Choice Questions
Question 1.
Which of the following is not the (RBSESolutions.com) measure of central tendency:
(A) Mean
(B) Median
(C) Mode
(D) Standard devitation
Solution :
(D) is correct.

Question 2.
In calculating mean of grouped data we assumed that frequencies: [NCERT Exemplar Problem]
(A) equally distribution In all classes
(B) centralized on sign of groups
(C) centralized on upper limits of classes
(D) centralized on lower limits of classes.
Solution :
(B) is correct.

Question 3.
If x_i are mid-point of class-intervals of grouped data f_i are their (RBSESolutions.com) corresponding frequencies and \(\overline { x }\) is mean, then Σ(f_ix_i – \(\overline { x }\)) equals: [NCERT Exemplar Problem]
(A) 0
(B) -1
(C) 1
(D) 2
Solution :
(A) is correct.

Question 4.
Cumulative frequency table is helpful in: [NCERT Exemplar Problem]
(A) Mean
(B) Mode
(C)Median
(D) None of these
Solution :
(C) is correct.

Question 5.
In given formula \(\overline { x }\) = a+h\(\left( \frac { { \Sigma f }_{ i }{ u }_{ i } }{ { \Sigma f }_{ i } } \right)\), value of u_i will be : [NCERT Exemplar Problem]
(A) h(x_i – a)
(B) \(\frac { { x }_{ i }-a }{ h }\)
(C) \(\frac { { a-x }_{ i } }{ h }\)
(D) \(\frac { { x }_{ i }+a }{ h }\)
Solution :
Thus (B) is correct.

Question 6.
For distribution :

Sum of lower limits of median class and (RBSESolutions.com) modal class is: [NCERT Exemplar Problem]
(A) 15
(B) 25
(C) 30
(D) 35
Solution :
Cumulative frequency just above 33 is 37 and its corresponding class interval is 10 – 15.
So modal class = 10 – 15.
Thus, sum of lower limit of median class and modal class
= 10 + 15 = 25, so (B) is correct.

Question 7.
For distribution :

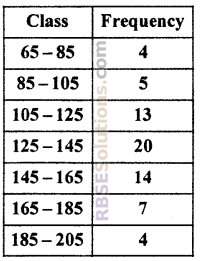
Difference between upper limit of (RBSESolutions.com) median class and lower limit of modal class is.
(A) 0
(B) 19
(C) 20
(D) 38
Solution :
In given data, maximum frequency is 20 and its corresponding class-interval is 125 – 145.
Thus modal class will be 125 – 145.
For median,
cumulative frequency just above 33 is 37 and its corresponding class-interval is 10 – 15.
So median class = 10 – 15
cumulative frequency table

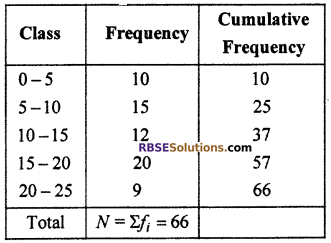
Here N = 66 ⇒ \(\frac { N }{ 2 }\) = \(\frac { 66 }{ 2 }\) = 33
Difference between upper limit of median (RBSESolutions.com) class and lower limit of modal class
= 145 – 125 = 20.
Cumulative frequency just above 33.5 is 42
whose corresponding class interval is 125 – 145.
So median class = 125 – 145 =20
Thus, (C) is correct.

Question 8.
To find mean from grouped data on the formula \(\overline { x }\) = a + \(\frac { { \Sigma f }_{ i }{ d }_{ i } }{ { \Sigma f }_{ i } } \) d_i is deviation of (RBSESolutions.com) following from a. [NCERT Exemplar Problem]
(A) Lower limits of classes
(B) Upper limits of classes
(C) Mid-points of classes
(D) Frequencies of group sign
Solution :
(C) is correct

Question 9.
The average of n observation is \(\overline { X }\). If we add 1 in first term, 2 in second term similarly 3, 4, 5, ………., n, then new mean will be:
(A) \(\overline { X }\) + n
(B) \(\overline { X }\) + \(\frac { n }{ 2 }\)
(C) \(\overline { X }\) + \(\frac { n+1 }{ 2 }\)
(D) None of these
Solution :
(C) is correct.

Question 10.
Number of students in a school (RBSESolutions.com) according to their age are as follows:

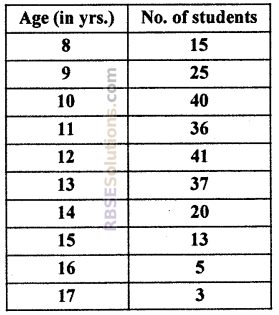
Their mode is:
(A) 41
(B) 12
(C) 3
(D) 17.
Solution :
From above table it is clear that (RBSESolutions.com) frequency 41 is maximum and its corresponding age group of 12. So its mode will be 12.
Thus (B) is correct

Question 11.
The average of statistical data is called:
(A) Arithmetic Mean
(B) Median
(C) Mode
(D) Frequency
Solution :
(A) is correct.

Question 12.
If 9 is mean of 5, 7, 9, x then find x.
(A) 11
(B) 15
(C) 18
(D) 16.
Solution :

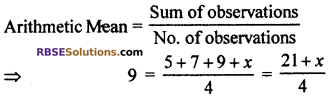
⇒ 36 = 21 + x
⇒ x = 36 – 21 = 15
Thus, (B) is correct.

Short/Long Answer Type Questions

Question 1.
Find median of (RBSESolutions.com) following data
25, 34, 31, 23, 22, 26, 35, 28, 20, 32
Solution :
Arranging given data in ascending order
20, 22, 23, 25, 26, 28, 31, 32, 34, 35
Here total terms (n) = 10 (even number)

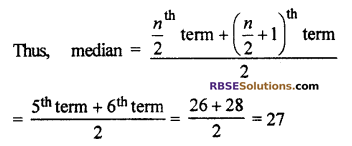
Thus, median = 27

Question 2.
The mean of 20 observation is 20. If 2 is added in each of first ten observation, then find mean of 20 new observations.
Solution :
Sum of 20 observations 20 × 20 = 400
2 is added in 10 observation so total increase = 10 × 2 = 20
Sum of total 20 observations = 400 + 20 = 420
Thus new arithmetic mean = \(\frac { 420 }{ 20 }\) = 21

Question 3.
If \(\overline { x }\) is mean of x₁, x₂ ….. x_n, then find (RBSESolutions.com) mean of mx₁, mx₂ ….. mx_n.
Solution :

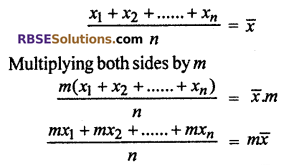
Thus, required mean = m\(\overline { x }\)

Question 4.
If \(\overline { x }\) is mean of x₁, x₂ ….. x_n, then prove that if a is added to (RBSESolutions.com) each term then mean will be (\(\overline { x }\)+a)
Solution :

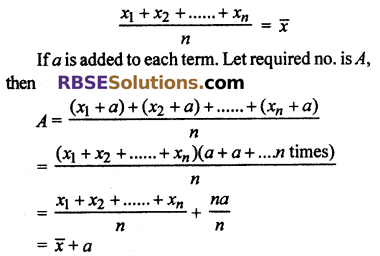
Question 5.
If median of 17, 26, 60, 45, 33 is 33 and if 17 is replaced by 27 then (RBSESolutions.com) what will be new median?
Solution :
If 17 replaced by 27 then numbers will be 27, 26, 60, 45, 33 writing in ascending order 26, 27, 33, 45, 60.
Here n =5 (odd number)
Median = \({ \left( \frac { n+1 }{ 2 } \right) }^{ th }\) term
= \({ \left( \frac { 5+1 }{ 2 } \right) }^{ th }\) term = \(\left( \frac { { 6 }^{ th } }{ 2 } \right) \) term
= 3rd term = 33
∴ Median = 33

Question 6.
If arithmetic mean of following data (RBSESolutions.com) is 15 then find p.

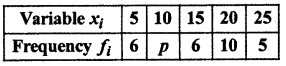
Solution :
Table for calculating A.M

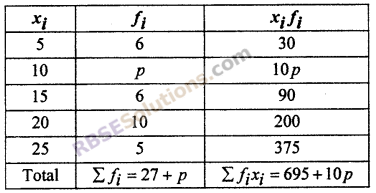
Thus, A.M. (\(\overline { x }\)) = \(\frac { \Sigma fx }{ \Sigma f } \)
15 = \(\frac { 695+10P }{ 27+P }\)
⇒ (27 + p)15 = 695 + 10P
⇒ 405 + 15P = 695 + 10P
⇒ 15P – 10P = 695 – 405
⇒ 5P = 290
⇒ P = \(\frac { 290 }{ 5 }\) = 58

Question 7.
Find mean of the following (RBSESolutions.com) distribution :

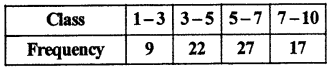
Solution :

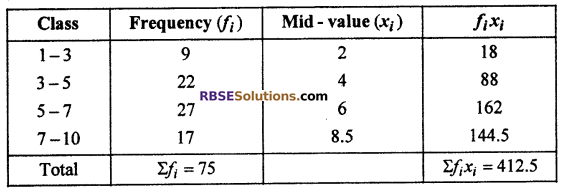
Thus, arithmetic mean (\(\overline { x }\)) = \(\frac { { \Sigma f }_{ i }{ x }_{ i } }{ { \Sigma f }_{ i } }\) = \(\frac { 412.5 }{ 75 }\) = 5.5

Question 8.
Consider the following distribution of daily wages of 40 workers of a factory (RBSESolutions.com) and by using suitable method, find mean daily wages of the workers of this factory :

Solution :

Arithmetic mean = \(\frac { { \Sigma f }_{ i }{ x }_{ i } }{ { \Sigma f }_{ i } }\) = \(\frac { 1980 }{ 40 }\) = 49.50
Thus, mean of daily wages = ₹ 49.50

Question 9.
Calculate the mean of the (RBSESolutions.com) following data : [NCERT Exemplar Problem]

Solution :
Here class-interval is discontinuous but if we convert it into continuous form, mid-values will not change so we will not change class-intervals.

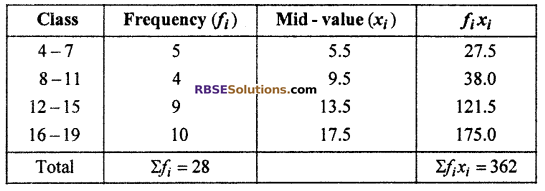
Thus, arithmetic mean (\(\overline { x }\)) = \(\frac { { \Sigma f }_{ i }{ x }_{ i } }{ { \Sigma f }_{ i } }\) = 12.93

Question 10.
Weight of 30 students of a class at the time of medical (RBSESolutions.com) test is recorded as per table given below

Find mean weight of students. [Board of Secondary Education Raj 2012]
Solution :
Let assumed mean (A) = 57.5

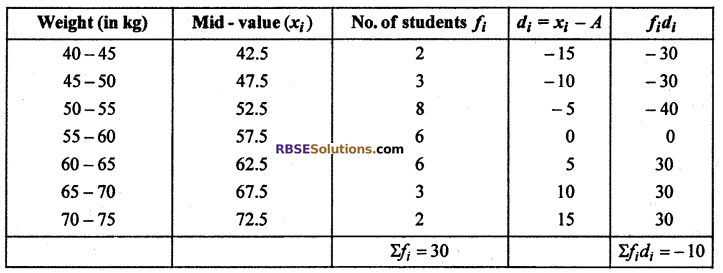
Arithmetic mean (\(\overline { x }\)) = A + \(\frac { { \Sigma f }_{ i }{ d }_{ i } }{ { \Sigma f }_{ i } } \) = 57.5 + \(\frac { -10 }{ 30 }\) = 57.167 = 57.17 kg.
Thus, mean weight of students = 57.17 kg.

Question 11.
To find concentration (part per million) of (SO₂) Sulphur dioxide in air (RBSESolutions.com) data ¡s collected from 30 colonies of a city which are given below:

Find mean of concentration of SO₂ in Air.
Solution :

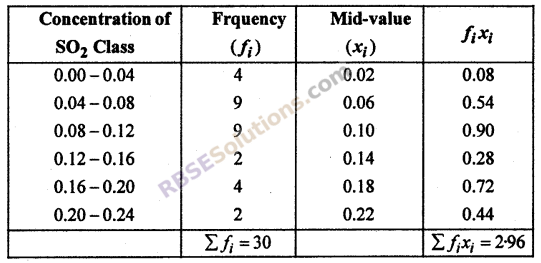
Arithmetic mean (\(\overline { x }\)) = \(\frac { { \Sigma f }_{ i }{ d }_{ i } }{ { \Sigma f }_{ i } } \) = \(\frac { 2.96 }{ 30 }\) = 0.0986 or 0.099 (approx)
Thus, mean of concentration of SO₂ in Air = 0.099 part per million.

Question 12.
Following distribution respresents weight of 30 students in a class. Find (RBSESolutions.com) median weight of students.

Solution :

Here, N = 30 and \(\frac { N }{ 2 }\) = \(\frac { 30 }{ 2 }\) = 15 C.f. just above 15 is 19 and corresponding class-mterval is 55 – 60.
∴ Median class = 55 – 60
∴ l = 55, \(\frac { N }{ 2 }\) = 15, C = 13, f = 6 and h = 5

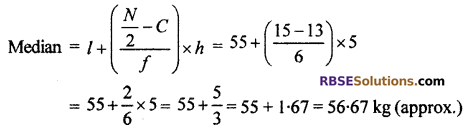
Thus, median weight of students = 56.67 kg(approx)

Question 13.
Following data represents life period observations (RBSESolutions.com) of electrical instruments.

Find mode of life period of instruments.
Solution :
Here maximum frequency is 61 and its corresponding class-interval is 60 – 80. So modal class = 60 – 80.
l = 60, f₁ = 61, f₀ = 52, f₂ = 38 and h = 20

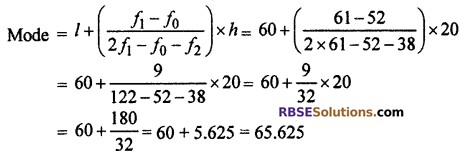
Thus, mode of life period is 65.625 hrs

Question 14.
Find mode of the (RBSESolutions.com) following data : (CBSE 2013)

Solution :
Here maximum frequency is 12 whose class is 60 – 80. So modal class 60 – 80
∴ l = 60, h = 20, f₁ = 12, f₀ = 10, f₂ = 6

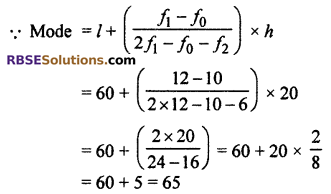
Thus, required mode = 65

Question 15.
Find mode of the following (RBSESolutions.com) data. (CBSE 2014)

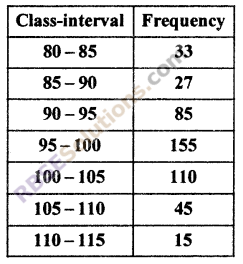
Solution :
Here maximum frequency = 155
whose class is 95 – 100
∴ l = 95, f₁ = 155, f₀ = 85, f₂ = 110, h = 5

Thus, required mode = 98.04

Question 16.
Find unknown frequency in the (RBSESolutions.com) following data of N = 100 and median = 32. (CBSE 2013)

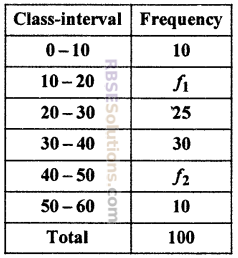
Solution :
Let f₁ and f₂ are unknown frequence, then

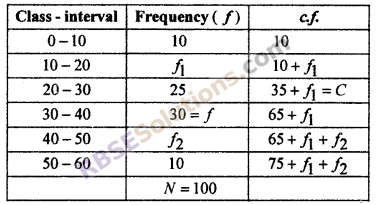
Thus, 75 + f₁ + f₂ = 100
f₁ + f₂ = 100 – 75 = 25
Given: Median = 32
So, median class is 30 – 40.
Thus, l = 30, h = 10, f = 30, C = 35 + f₁

15 – f₁ = 6
f₁ = 15 – 6 = 9
From eqn.(i), f₂ = 16
Thus, f₁ = 9, f₂ = 16

Question 17.
If mean of following (RBSESolutions.com) data is 21.5, then find K. (CBSE 2012)

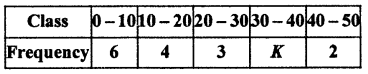
Solution :

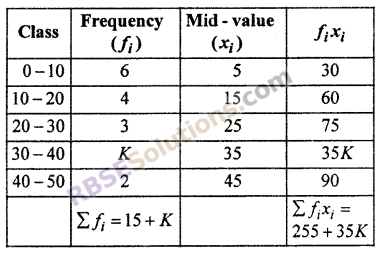
∵ Arithmetic mean = \(\frac { { \Sigma f }_{ i }{ x }_{ i } }{ { \Sigma f }_{ i } }\)
21.5 = \(\frac { 255+35K }{ 15+K }\)
⇒ 322.5 + 21.5 = 255 + 35K
⇒ 322.5 – 255 = 35K – 21.5K
⇒ 13.5K = 67.5
K = \(\frac { 67.5 }{ 13.5 }\) = 5
∴ K = 5

Question 18.
If median of given data is 28.5 then find the (RBSESolutions.com) values of x and y. [Board of Secondary Education Raj. 2014]

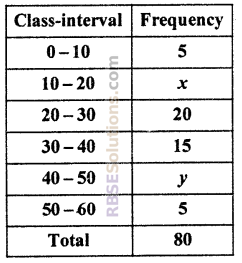
Solution :

cumulative frequency table
But sum of frequency Σf_i = N = 80 which is equal (RBSESolutions.com) to last term of c.f. group
∴ 45 + x + y = 80 or x + y = 80 – 45
⇒ x + y = 35 …(i)
Now \(\frac { N }{ 2 }\) = \(\frac { 80 }{ 2 }\) = 40
and median of distribution = 28.5 which lies in class-interval 20 – 30.
Median class = 20 – 30
l = 20, f = 20, c = 5 + x and h = 10

57 = 75 – x or x = 18
Putting value of x in eqn. (i), 18 + y = 35
Thus, y = 17.

Question 19.
If mean of given distribution is 50, then find the (RBSESolutions.com) values of x and y. [Board of Secondary Raj. 2014]

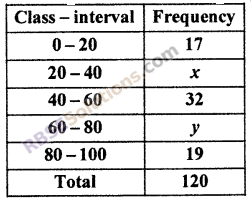
Solution :

But sum of frequencies is Σf_i = N = 120 which is equal (RBSESolutions.com) to last term of cumulative frequency group.
68 + x + y = 120
x + y = 120 – 68
x + y = 52
Now, \(\frac { N }{ 2 }\) = \(\frac { 120 }{ 2 }\) = 60
And median of distribution is equal to 50, which lies in class-interval 40 – 60.
Median class = 40 – 60
l = 40, f = 32, c = 17 + x and h = 20

⇒ 50 = 320 + 215 – 5x
⇒ 400 – 535 = – 5x
⇒ 5x = 135
⇒ x = 27 ……(i)
From equation (i) and (ii)
27 + y = 52
y = 25

Question 20.
Median of following data is 525. If sum of frequencies is 100, then (RBSESolutions.com) find values of x and y. (Board of Secondary Raj. 2012)

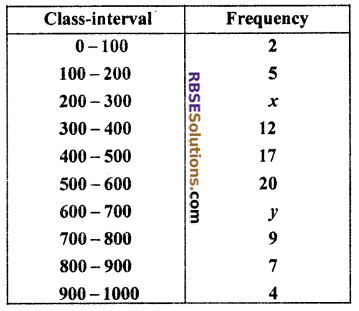
Solution :

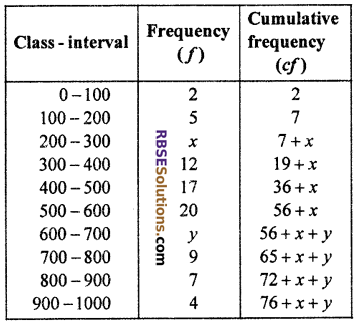
Given: Σf = N = 100
Thus, 76 + x + y = 100
⇒ x + y = 100 – 76 = 24 …..(i)
Median is 525 which (RBSESolutions.com) lies in 500 – 600.
∴ l = 500; f = 20, c = 36 + x, and h = 100


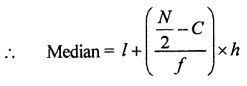
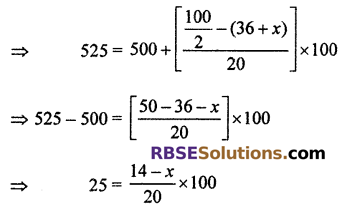
⇒ 25 = (14 – x) × 5
⇒ 14 – x = \(\frac { 25 }{ 5 }\) = 5
⇒ x = 14 – 5
∴ x = 9
From equation (i), 9 + y = 24
⇒ y = 24 – 9
∴ y = 15
Thus, x = 9 and y = 15.

Question 21.
If median of the following distribution is 27, then (RBSESolutions.com) find the values of x and y. [CBSE 2012]

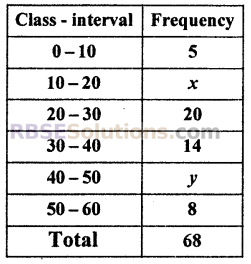
Solution :

Given: N = 68
⇒ 47 + x + y = 68
⇒ x + y = 68 – 47
⇒ x + y = 21 ……..(i)
Now \(\frac { N }{ 2 }\) = \(\frac { 68 }{ 2 }\) = 34
Median of distribution is 27 which (RBSESolutions.com) lies is class-interval 20 – 30.
∴ Median class 20 – 30
l = 20, c = 5 + x, f = 20 and h = 10

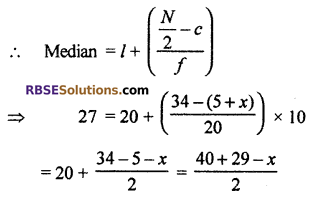
⇒ 69 – x = 2 × 27
⇒ x = 69 – 54 = 15
Putting value of x in eqn. (i),
15 + y = 21
⇒ y = 21 – 15 = 6
Thus, x = 15, y = 6

Question 22.
Following table shows the age of (RBSESolutions.com) patients admit in Hospital :

Find mode and mean. Compare two central measures and explain. them. (NCERT)
Solution :
For Mode : Here maximum frequency is 23 and its corresponding class is 35 – 45.
So, modal class 35 – 45
∴ l = 35, f₀ = 21, f₁ = 23, f₂ = 14, h = 10

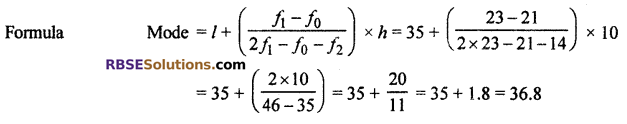
Thus, mode = 36.8 yrs.
For Mean : Let assumed (RBSESolutions.com) mean A = 40

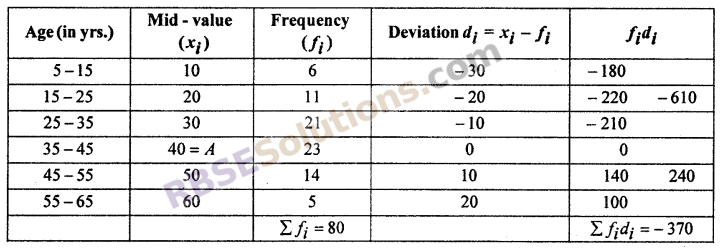
∵ Arithmetic mean (\(\overline { x }\)) = A + \(\frac { { \Sigma f }_{ i }{ d }_{ i } }{ { \Sigma f }_{ i } } \) = 40 – \(\frac { 370 }{ 80 }\) = 40 – 4.625 = 35.375
Thus, mode of data = 36.8 years. and mean = 35.375 years.
Maximum age of patients admit in hospital is 36.8 years. where as average age of patients admit is hospital is 35.57 yrs.

Question 23.
Following table represents literacy rate of 35 cities (RBSESolutions.com) in percentage.

Find mean literacy rate.
Solution :
Let assumed mean (A) 70
Class size (h) = 55 – 45 = 10
By step deviation method

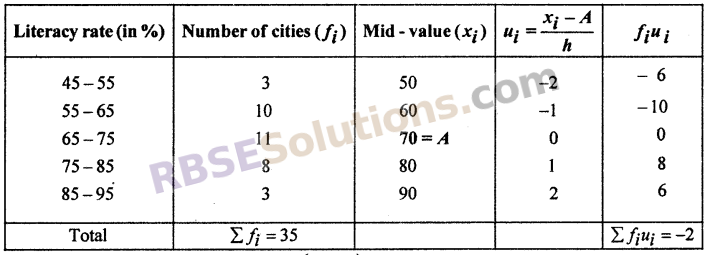
Mean (\(\overline { x }\)) = A + \(\left( \frac { { \Sigma f }_{ i }{ u }_{ i } }{ { \Sigma f }_{ i } } \right)\) × h
⇒ \(\overline { x }\) = 70 + \(\frac { -2 }{ 35 }\) × 10 = 70 + \(\frac { -20 }{ 35 }\)
= 70 + (-0.57) = 70 – 0.57 = 69.43
Thus, mean literacy rate = 69.43%

Question 24.
The distribution of marks obtained by 30 students in (RBSESolutions.com) Maths examination as follows :

Find mean from assumed mean method for given data also find mode.
Solution :
Let assumed mean (A) = 47.5

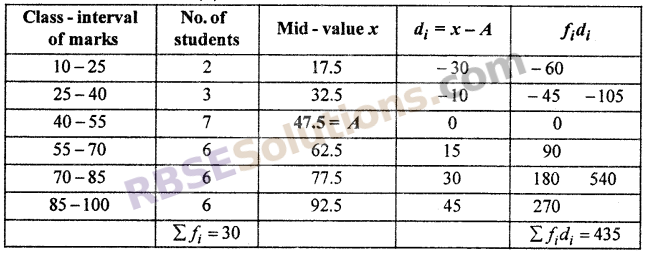
∵ Arithmetic mean (\(\overline { x }\)) = A + \(\frac { { \Sigma f }_{ i }{ d }_{ i } }{ { \Sigma f }_{ i } } \) = 47.5 + \(\frac { 435 }{ 30 }\) = 47.5 + 14.5 = 62
From given table, if is clear that maximum (RBSESolutions.com) frequency is 7 and its corresponding class is 40 – 55.
Thus, modal class will be 40 – 55.
∵ l = 40, f₀ = 3, f₁ = 7, f₂ = 6, and h = 15

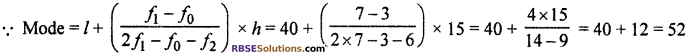
Thus, mean = 62 and mode = 52

Question 25.
Following frequency distribution represents electricity cost of 68 users in a colony. Find mean, median and mode from these data:

Solution :
For median :

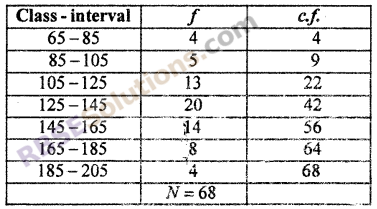
Here, N = 68 \(\frac { N }{ 2 }\) = \(\frac { 68 }{ 2 }\) = 34
Cumulative frequency (RBSESolutions.com) just above 34 is 42 and its corresponding class is 125 – 145.
∴ Median class = 125 – 145, here l = 125, N = 68, f = 20, C = 22, and h = 20

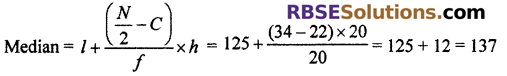
For mean : Let assumed mean (A) = 135, h = 20

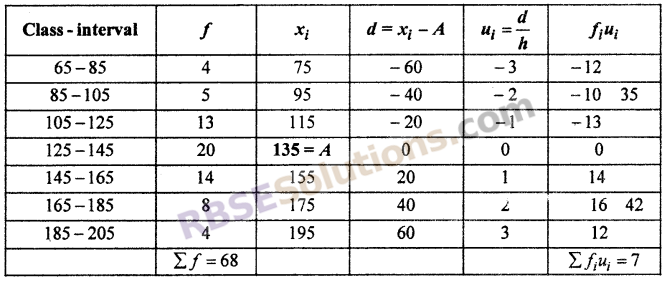
Mean = A + \(\frac { { \Sigma f }_{ i }{ u }_{ i } }{ { \Sigma f }_{ i } }\) × h = 135 + \(\frac { 7 }{ 68 }\) × 20
= 135 + 0.1029 × 20 = 135 + 2.05 = 137.05
For mode : In given data, maximum (RBSESolutions.com) frequency is 20 and its corresponding class is 125 – 145.
Modal class = 125 – 145
Here l = 125, f₁ = 20, f₀ = 13, f₂ = 14 and h = 20

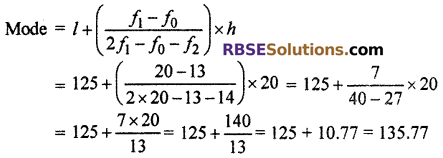
Hence, median = 137, mean = 137.05 and mode = 135.77

We hope the given RBSE Solutions for Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 17 Measures of Central Tendency Additional Questions, drop a comment below and we will get back to you at the earliest.