RBSE Solutions for Class 10 Maths Chapter 2 Real Numbers Ex 2.3 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 2 Real Numbers Exercise 2.3.
| Board | RBSE |
| Te×tbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Real Numbers |
| E×ercise | Exercise 2.3 |
| Number of Questions Solved | 3 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 2 Real Numbers Ex 2.3
RBSE Solutions For Class 10 Maths Chapter 2 Question 1.
Prove that 5 – √3 is (RBSESolutions.com) irrational.
Solution
Let 5 – √3 is a rational number.
we have to find out two integers a and b such as
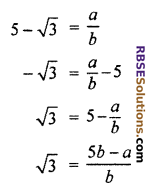
a, b and 5 all are integers
\(\frac { 5b-a }{ b }\) is a rational number.
√3 will be also rational number.
But this contradicts the fact that √3 is an irrational number.
So our hypothesis is wrong.
Hence, 5 – √3 is an irrational number.
Hence proved.
RBSE Solutions For Class 10 Maths Question 2.
Prove that following (RBSESolutions.com) numbers are ir-rational
(i) \(\frac { 1 }{ \surd 2 }\)
(ii) 6 + √2
(iii) 3√2
Solution
(i) \(\frac { 1 }{ \surd 2 }\) is a rational number
we find two integers b such as \(\frac { 1 }{ \surd 2 }\) = \(\frac { a }{ b }\)
where a and b co-prime integers (b ≠ 0)
Square both sides
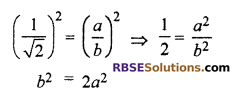
So, b2 divides by 2.
.’. So, b also divides by 2.
Now let b = 2c, where c is any integer
b2 = (2c)2
⇒ b2 = 4c2
⇒ 2a2 = 4c2 (∴ b2 = 2a2)
⇒ a2 = 2c2
Hence, a2, divides by 2.
a also divides by 2.
Hence, 2 is a common (RBSESolutions.com) factor of a and b.
But, this contradicts the fact that a and b have no common factor other than 1.
This contradiction arises by assuming that \(\frac { 1 }{ \surd 2 }\) is rational,
Hence \(\frac { 1 }{ \surd 2 }\) is a irrational number.
Hence proved
(ii) Let 6 + √2 is a rational number
we can find two integers a and b (b ≠ 0)
Such as
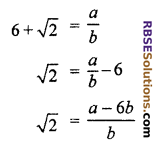
a, b and 6 all are integers.
\(\frac { a-6b }{ b }\) is a rational numbers
√2 is also a rational number
But this contradicts the fact that √2 is an irrational number.
Our hypothesis is wrong.
Hence, 6 + √2 is an irrational number.
Hence proved.
(iii) Let 3√2 is a rational number we (RBSESolutions.com) find two integers a and b such as
3√2 = \(\frac { a }{ b }\) (where a and b co-prime integers)
⇒ √2 = \(\frac { a }{ 3b }\)
⇒ a, b and 3 are integers.
\(\frac { a }{ 3b }\) is a rational number
√2 is a rational number
3√2 will be also a rational numbers.
But this contradicts the fact that √2 is an irrational number.
So, our hypothesis is wrong.
So, 3√2 is an irrational number.
Hence proved.
RBSE Solutions Of Class 10 Maths Question 3.
If p and q are a positive prime number (RBSESolutions.com) then prove that √p + √q is irrational.
Solution
Let √p + √q is a rational number

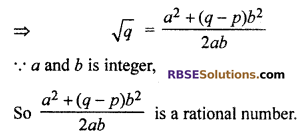
√q is also a (RBSESolutions.com) rational number.
But this result is contradicted.
So our hypothesis is wrong.
Hence, √p + √q is an irrational number.
Hence proved.
We hope the given RBSE Solutions for Class 10 Maths Chapter 2 Real Numbers Ex 2.3 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 2 Real Numbers Exercise 2.3, drop a comment below and we will get back to you at the earliest.