RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.2

by

RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Exercise 3.2.

Board RBSE
Te×tbook SIERT, Rajasthan
Class Class 10
Subject Maths
Chapter Chapter 3
Chapter Name Polynomials
E×ercise Exercise 3.2
Number of Questions Solved 4
Category RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Ex 3.2

RBSE Solutions For Class 10 Maths Chapter 3 Question 1.
Using division algorithm, (RBSESolutions.com) find quotient and remainder dividing f(x) by g(x).
(i) f(x) = 3x3 + x2 + 2x + 5, g(x) = 1 + 2x + x2
(ii) f(x) = x3 – 3x2 + 5x + 3, g(x) = x2 – 2
(iii) f(x) = x3 – 6x2 + 11x – 6, g(x) = x + 2
(iv) f(x) = 9x4 – 4x2 + 4, g(x) = 3x2 + x – 1
Solution
(i) Given : f(x) = 3x3 + x2 + 2x + 5
and g(x) = 1 + 2x + x2
or g(x) = x2 + 2x + 1
Dividing f(x) by g(x)
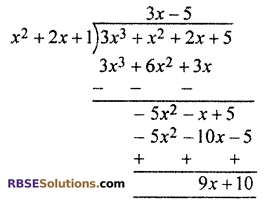
RBSE Solutions For Class 10 Maths Chapter 3 Polynomials
Quotient q(x) = 3x – 5
Remainder r(x) = 9x + 10
Here, Quotient × Divisor + Remainder
(3x – 5) (1 + 2x + x2) + 9x + 10
= 3x + 6x2 + 3x3 – 5 – 10x – 5x2 + 9x + 10
= 3x3 + x2 – 7x – 5 + 9x + 10
= 3x3 + x2 + 2x + 5.
= dividend
Thus division (RBSESolutions.com) algorithm is verified.

(ii) given f(x) = x3 – 3x2 + 5x – 3
and g(x) = x2 – 2
Dividing f(x) by g(x)
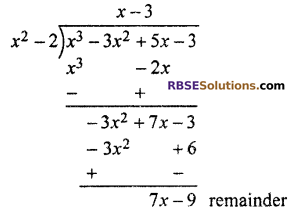
RBSE Class 10 Maths Exercise 3.2 Solutions Polynomials
Quotient q(x) = x – 3
Remainder r(x) = 7x – 9
By Euclid divison algorithm
f(x) = g(x).q(x) + r(x)
= (x2 – 2)(x – 3) + 7x – 9
= x3 – 3x2 – 2x + 6 + 7x – 9
= x3 – 3x2 + 5x – 3
= f(x)
Thus division (RBSESolutions.com) algorithm is verified.
(iii) Given f(x) = x3 – 6x2 + 11x – 6
and g(x) = x + 2
Dividing f(x) by g(x)
Ex 3.2 Class 10 RBSE Polynomials
Quotient q(x) = x2 – 8x + 27
Remainder r(x) = -60
Here, Divisor × Quotient + Remainder
(x + 2) (x2 – 8x + 27) – 60
= x3 + 2x2 – 8x2 – 16x + 27x + 54 – 60
= x3 – 6x2 + 11x – 6
= dividend
Hence, division (RBSESolutions.com) algorithm is verified.
(iv) Given f(x) = 9x4 – 4x2 + 4
and g(x) = 3x2 + x – 1
Dividing f(x) by g(x)
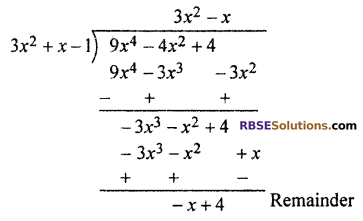
RBSE Class 10 Maths Chapter 3 Solutions Polynomials
Thus quotient q(x) = 3x2 – x
Remainder f(x) = -x + 4
Here : f(x).q(x) + f(x)
= (3x2 + x – 1) (3x2 – x) + (-x) + 4
= 9x4 + 3x3 – 3x2 – 3x3 – x2 + x – x + 4
= 9x4 – 4x2 + 4
= f(x)
Thus, division (RBSESolutions.com) algorithm is verified.

RBSE Class 10 Maths Exercise 3.2 Solutions Question 2.
Dividing second polynomial by first polynomial and test whether first polynomial is a factor of second polynomial.
(i) f(x) = x2 + 3x + 1 ,f(x) = 3x4 + 5x3 – 7x2 + 2x + 2
(ii) g(t) = t2 – 3, f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
(iii) g(x) = x3 – 3x + 1, f(x) = x5 – 4x3 + x2 + 3x + 1
Solution
(i) Given, f(x) = 3x4 + 5x3 – 7x2 + 2x + 2
g(x) = x2 + 3x + 1
If by dividing f(x) by g(x), we get (RBSESolutions.com) remainder as 0, then g(x) will be factor of f(x).
Dividing f(x) by g(x),
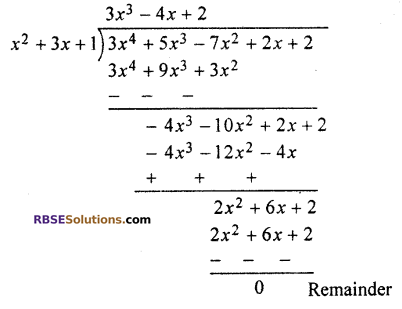
RBSE Solutions For Class 10 Maths Chapter 3.2 Polynomials
Remainder is zero.
By division (RBSESolutions.com) algorithm theorem
3x4 + 5x3 – 7x2 + 2x + 2 = (x2 + 3x + 1) (3x3 – 4x + 2) + 0
Thus, x2 + 3x + 1 is a factor of 3x4 + 5x3 – 7x2 + 2x + 2
(ii) Given,
f(t) = 2t4 + 3t3 – 2t2 – 9t – 12
g(t) = t2 – 3
Dividing f(x) by g(x), If remainder is (RBSESolutions.com) zero then g(x) will be a factor of f(x).
Dividing f(x) by g(x)
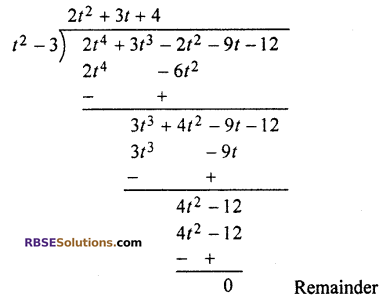
10th Class Maths Polynomials Exercise 3.2 Solutions Polynomials
Remainder is zero
By division (RBSESolutions.com) algorithm theorem
2t4 + 3t3 – 2t2 – 9t – 12 = (t2 – 3) (2t2 + 3t + 4) + 0
Therefore t2 – 3 is a factor of 2t4 + 3t3 – 2t2 – 9t – 12
(iii) Given
f(x) = x5 – 4x3 + x2 + 3x + 1
g(x) = x3 – 3x + 1
If dividing f(x) by g(x) we get remainder 0 then g(x) will be a factor of f(x).
Dividing f(x) by g(x),
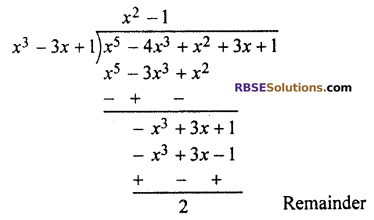
RBSE Class 10 Maths Chapter 3 Polynomials
Remainder r(x) = 2
Quotient q(x) = x2 – 1
Remainder is not zero.
Therefore g(x) is (RBSESolutions.com) not a factor of f(x).

Ex 3.2 Class 10 RBSE Question 3.
Following are the polynomials with their zeros, find all the other zeros.
(i) f(x) = 2x4 – 3x3 – 3x2 + 6x – 2; √2 and -√2
(ii) f(x) = x4 – 6x3 – 26x2 + 138x – 35; 2 ± √3
(iii) f(x) = x3 + 13x2 + 32x + 20; -2
Solution
(i) Given
f(x) = 2x4 – 3x3 – 3x2 + 6x – 2
Two zeros of (RBSESolutions.com) polynomial f(x) are √2 and -√2
(x – √2)(x + √2) = x2 – 2, will be a factor of f(x).
Dividing polynomial f(x) by x2 – 2
Polynomials Class 10 Exercise 3.2 Polynomials
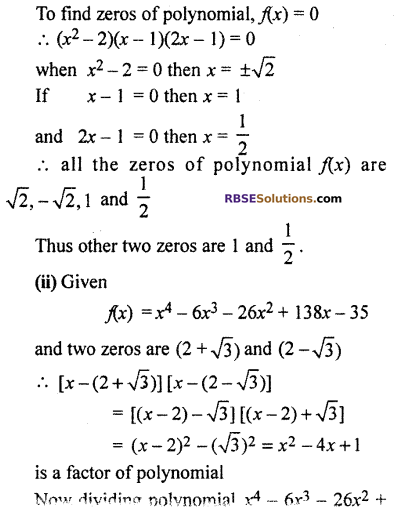
Polynomials Class 10 RBSE Polynomials
Class 10 Maths Chapter 3 Polynomials Exercise 3.2 Polynomials
Now other (RBSESolutions.com) zeros of polynomail
If x + 5 = 0 then x = -5
or x – 7 = 0 then x = 7
Other zeros of polynomail are -5 and 7
(iii) Given
f(x) = x3 + 13x2 + 32x + 20 and one zero is -2
(x + 2) will be factor of f(x)
Now, dividing f(x) by x + 2
RBSE Solutions For Class 10 Maths Chapter 3 Exercise 3.2 Polynomials
Thus f(x) = (x + 2)(x2 + 11x + 10)
= (x + 2)[x2 + 10x + x + 10]
= (x + 2)[x(x + 10) + 1(x + 10)]
= (x + 2)(x + 10)(x + 1)
Now, other zeros of polynomial
If x + 10 = 0 then x = -10
or x + 1 = 0 then x = -1
Thus, other zeros of polynomial are -10, -1

RBSE Class 10 Maths Chapter 3 Solutions Question 4.
Dividing polynomiaal f(x) = x3 – 3x2 + x + 2 by polynomial g(x). (RBSESolutions.com) Quotient q(x) and re-mainder r(x) are obtained as x – 2 and -2x + 4 respectively. Find polynomial g(x).
Solution
Dividend f(x) = x3 – 3x2 + x + 2
divisor g(x) = to find
quotient q(x) = x – 2
remainder r(x) = -2x + 4
By Euclid division theorem
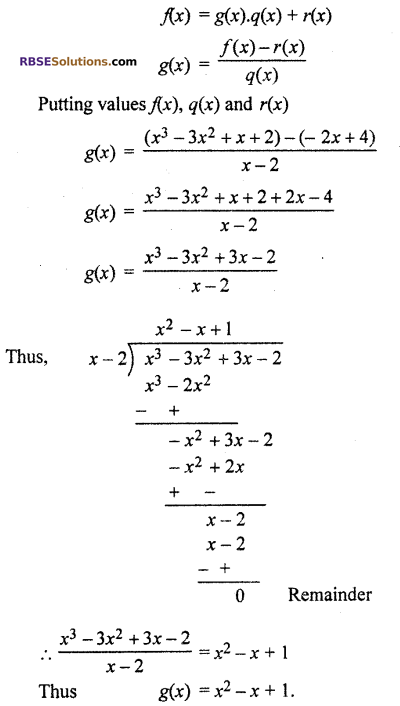
RBSE Class 10 Maths Chapter 3 Exercise 3.2 Polynomials

We hope the given RBSE Solutions for Class 10 Maths Chapter 3 Polynomials Ex 3.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 Polynomials Exercise 3.2, drop a comment below and we will get back to you at the earliest.