RBSE Solutions for Class 10 Maths Chapter 3 बहुपद Ex 3.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 3 बहुपद Exercise 3.2.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | बहुपद |
| Exercise | Exercise 3.2 |
| Number of Questions Solved | 4 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 3 बहुपद Ex 3.2
प्रश्न 1.
विभाजन एल्गोरिथ्म का प्रयोग करके f(x) को g(x) से भाग देने (RBSESolutions.com) पर भागफल तथा शेषफल ज्ञात कीजिए
(i) f(x) = 3x2 + x2 + 2x + 5, g(x) = 1 + 2x + x2
(ii) f(x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2
(iii) f(x) = x3 – 6x2 + 11x – 6, g(x) = x + 2
(iv) f(x) = 9x4 – 4x2 +4, g(x) = 3x2 + x – 1
हल:
(i) हम सर्वप्रथम भाजक एवं भाज्य के पदों की घटती हुई घातों के क्रम में व्यवस्थित करते हैं । यहाँ पर भाज्य पहले से ही मानक रूप में हैं तथा मानक रूप में भाजक x2 + 2x + 1 है।
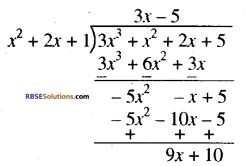
इसलिए भागफल 3x – 5 तथा शेषफल 9x + 10 होगा।
यहाँ— भागफल × भाजक + शेषफल
(3x – 5) (1 + 2x + x2) + 9x + 10
= 3x + 6x2 + 3x3 – 5 – 10x – 5x2 + 9x + 10
= 3x3 + x2 – 7x – 5 + 9x + 10
= 3x3 + x2 + 2x + 5
= भाज्य
अतः विभाजन एल्गोरिथ्म का प्रयोग सत्यापित होता है।
![]()
(ii) यहाँ भाज्य और भाजक दोनों मानक रूप (RBSESolutions.com) में हैं। इसलिए हमें प्राप्त है।
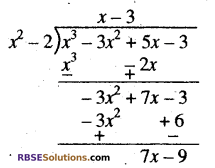
इसलिए भागफल x – 3 तथा शेषफल 7x – 9 होगा।
यहाँ- भागफल × भाजक + शेषफल
(x – 3) (x2 – 2) + 7x – 9
=x3 – 2x – 3x2 + 6 + 7x – 9
= x3 – 3x2 – 2x + 6 + 7x – 9
= x3 – 3x2 + 5x – 3
= भाज्य
अतः विभाजन एल्गोरिथ्म का प्रयोग सत्यापित होता है।
(iii) यहाँ पर भाज्य और भाजक दोनों (RBSESolutions.com) ही मानक रूप में हैं, हमें प्राप्त है।
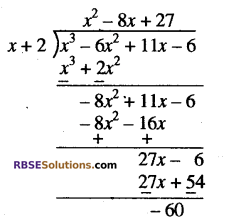
इसलिए भागफल x2 – 8x + 27 तथा शेषफल – 60 होगा।
यहाँ- भागफल × भाजक + शेषफल
(x2 – 8x + 27) × (x + 2) – 60
= x3 + 2x2 – 8x2 – 16x + 27x + 54 – 60
= x3 – 6x2 + 11 – 6
= भाज्य
अतः विभाजन एल्गोरिथ्म का प्रयोग सत्यापित होता है।
(iv) यहाँ पर भाज्य और भाजक (RBSESolutions.com) दोनों ही मानक रूप में हैं। हमें प्राप्त है।
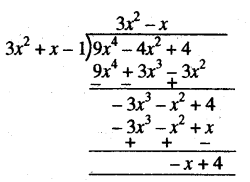
इसलिए भागफल 3x2 – x तथा शेषफल (-x + 4) होगा।
यहाँ- भागफल × भाजक + शेषफल
(3x2 – x) × (3x2 + x – 1) + (-x + 4)
= 9x4 + 3x3 – 3x2 – 3x3 – x2 + x – x + 4
= 9x4 – 4x4 +4
= भाज्य
अतः विभाजन एल्गोरिथ्म का प्रयोग सत्यापित होता है।
![]()
प्रश्न 2.
पहले बहुपद से दूसरे बहुपद को भाग करके, (RBSESolutions.com) जाँच कीजिए कि प्रथम बहुपद दूसरे बहुपद का एक गुणनखण्ड है
(i) g(s) = x2 + 3x + 1, f(x) = 3x4 + 5x3 – 7x2 + 2x + 2
(ii) g(t) = t2 – 3, f(t) = 2x4 + 3t3 – 2t2 – 9y – 12
(iii) g(x) = x3 – 3x + 1, f(x) = x5 – 4x3 + x2 + 3x + 1
हल
(i) 3x4 + 5x3 – 7x2 + 2x + 2 को x2 + 3x + 1 से भाग करने पर
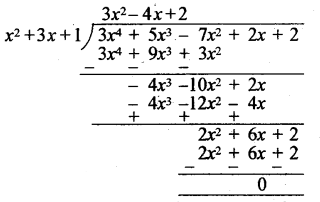
चूँकि, शेषफल शून्य है, अतः x2 + 3x + 1 बहुपद 3x4 + 5x3 – 7x2 + 2x + 2 को एक गुणनखण्ड है। उत्तर
(ii) 2t4 + 3t3 – 2t2 – 9t – 12 को t2 – 3 से भाग करने पर
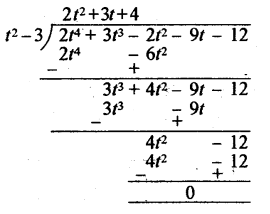
चूँकि, शेषफल शून्य है, अतः t2 – 3 बहुपद 2t4 + 3t3 – 2t2 – 9t – 12 का एक गुणनखण्ड है। उत्तर
(iii) x5 – 4x3 + x2 + 3x + 1 बहुपद को x3 – 3x + 1 से भाग करने पर
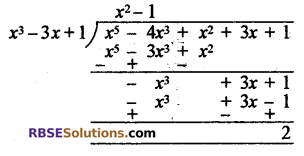
यहाँ शेषफल 2 है अर्थात् शेषफल शून्य (RBSESolutions.com) नहीं है अतः x3 – 3x + 1 बहुपद x5 – 4x3 + x2 + 3x + 1 का गुणनखण्ड नहीं है। उत्तर
![]()
प्रश्न 3.
निम्न बहुपदों के साथ उनके शून्यक दिये गये हैं, अन्य सभी शून्यक ज्ञात कीजिए
(i) f(x) = 2x4 – 3x3 – 3x2 + 6x – 2; \(\sqrt { 2 } \) और \(-\sqrt { 2 } \)
(ii) f(x) = x4 – 6x3 – 26x2 + 138r – 35; \(2\pm \sqrt { 3 } \)
(iii) f(x) = x3 + 13x2 + 32x + 20; – 2
हल:
(i) चूँकि x = α एक बहुपद का शून्यक है, तो (x – α) बहुपद f(x) का गुणनखण्ड होता है। चूँकि \(\sqrt { 2 } \) और \(-\sqrt { 2 } \) बहुपद f(x) के शून्यक हैं,
इसलिए \(\left( x-\sqrt { 2 } \right) \left( x+\sqrt { 2 } \right) ={ x }^{ 2 }-2\), बहुपद (x) का एक गुणनखण्ड है।
अब, हम f(x) = 2x4 – 3x3 – 3x2 + 6x – 2 के अन्य शून्यक ज्ञात करने के लिए इसको g(x) = x2 – 2 से विभाजित करते हैं।

(ii) चूँकि x = α एक बहुपद का (RBSESolutions.com) शून्यक है, तो (x – α) बहुपद f(x) का f(x) गुणनखण्ड होता है।
चूँकि \(\left( 2+\sqrt { 3 } \right) \) और \(\left( 2-\sqrt { 3 } \right) \) बहुपद f(x) के शून्यक हैं। इसलिए

(iii) चूंकि x = α एक बहुपद का, (RBSESolutions.com) शून्यक है, तो (x – α) बहुपद f(x) का गुणनखण्ड होता है, इसलिए (x + 2) बहुपद f(x) का एक गुणनखण्ड है।
अब, हम f(x) = x3 + 13x2 + 32x + 20 के अन्य शून्यक ज्ञात करने के लिए इसको g(x) = (x + 2) से विभाजित करते हैं।
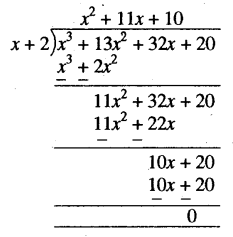
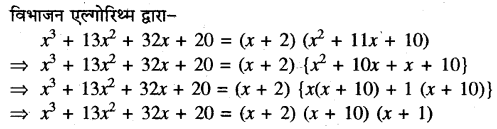
अतः दिये हुए बहुपद के शून्यक – 2, – 10 और – 1 हैं।
अतः बहुपद के अन्य शून्यक – 10 और – 1 हैं। उत्तर
![]()
प्रश्न 4.
बहुपद f(x) = x3 – 3x++ +2 को बहुपद g(x) से भाग देने (RBSESolutions.com)पर भागफल q(x) तथा शेषफल r(x) क्रमशः x-2 और – 2x +4 प्राप्त होता है तो बहुपद g(x) ज्ञात कीजिए।
हल:
बहुपद x3 – 3x2 + x + 2 को एक बहुपद g(x) से भाग देने पर भागफल (x – 2) व शेषफल – 2x +4 प्राप्त होता है।

![]()
इस प्रकार (RBSESolutions.com)समीकरण (i) से g(x) = x2 – x + 1 प्राप्त होता है। उत्तर
We hope the RBSE Solutions for Class 10 Maths Chapter 3 बहुपद Ex 3.2 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 3 बहुपद Exercise 3.2, drop a comment below and we will get back to you at the earliest.