RBSE Solutions for Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions

RBSE Solutions for Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions.

Board	RBSE
Textbook	SIERT, Rajasthan
Class	Class 10
Subject	Maths
Chapter	Chapter 4
Chapter Name	दो चरों वाले रैखिक समीकरण एवं असमिकाएँ
Exercise	Additional Questions
Number of Questions Solved	52
Category	RBSE Solutions

Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions

विविध प्रश्नमाला

प्रश्न 1.
k के किस मान के लिए समीकरण युग्म x + y – 4 = 0; 2x + ky – 3 = 0 का कोई (RBSESolutions.com) हल नहीं होगा
(क) 0
(ख) 2
(ग) 6
(घ) 8

प्रश्न 2.
के किस मान के लिए समीकरण युग्म 3x – 2y = 0 तथा kx + 5y = 0 के अनन्त हल होंगे
(क) \(\frac { 1 }{ 2 } \)
(ख) 3
(ग) \(\frac { -5 }{ 3 } \)
(घ) \(\frac { -15 }{ 2 } \)

प्रश्न 3.
समीकरण युग्म kx – y = 2; 6x – 2y = 3 का हल अद्वितीय होगा, यदि
(क) k = 2
(ख) k = 3
(ग) k ≠ 3
(घ) k ≠ 0

प्रश्न 4.
असमिकाओं x ≥ 0, y ≥ 0 के संगत समीकरण (RBSESolutions.com) व्यक्त करते हैं
(क) 3-अक्ष को
(ख) 1-अक्ष को
(ग) x एवं 1-अक्षों को।
(घ) x = 1 रेखा को

प्रश्न 5.
असमिका y – 3 ≤ 0 के संगत रेखा के लिए निम्न कथन सत्य है
(क) x-अक्ष के समान्तर है।
(ख) 1-अक्ष के समान्तर है
(ग) x-अक्ष को विभाजित करती है
(घ) मूल बिन्दु से गुजरती है।

उत्तर-तालिका
1. (ख) 2. (घ) | 3. (ग) 4. (ग) 5. (क)

प्रश्न 6.
निम्न रैखिक समीकरण युग्म के हलों की (RBSESolutions.com) संख्या लिखिए-
x + 2y – 8 = 0
2x + 4y = 16
हल:
x + 2y – 8 = 0 …..(i)
2x +4y = 16
या 2x + 4y – 16 = 0 …..(ii)
समीकरण (i) से a₁ = 1, b₁ = 2, c₁ = – 8
समीकरण (ii) से a₂ = 2, b₂ = 4, c₂ = – 16

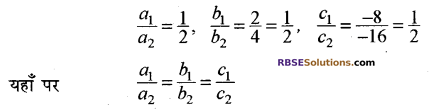
इसलिए रैखिक समीकरण युग्म के हल असीमित (अनन्त) होंगे एवं युग्म संगत होगा तथा रेखायें सम्पाती होंगी।

प्रश्न 7.
यदि समीकरण युग्म 2x + 3y = 7, (a + b)x + (2a – b)y = 21 के अनन्त हल हों तो a, b के मान (RBSESolutions.com) ज्ञात कीजिए।
हल:
दिये गये समीकरण युग्म के समीकरण हैं-
2x + 3y = 7
या 2x + 3y – 7 = 0 …..(i)
(a + b)x + (2a – b)y = 21
या (a + b)x + (2a – b)y – 21 = 0 …..(ii)
समीकरण (i) से हमें प्राप्त हैं-
a₁ = 2, b₁ = 3, c₁ = – 7
समीकरण (ii) से हमें प्राप्त हैं-
a₂ = (a + b), b₂ = (2a – b), c₂ = – 21
चूँकि दिया गया है कि दिये गये समीकरणों के युग्म के हल अनन्त हैं। (RBSESolutions.com) इसलिए अनन्त हल होने की शर्त का उपयोग करने पर।


इस प्रकार से हमें प्राप्त होता है- a = 5, b = 1
अतः a = 5 और b = 1 अभीष्ट हल हैं। उत्तर

प्रश्न 8.
असमिका | x | ≤ 3 के हल समुच्चय को छायांकित (RBSESolutions.com) कीजिए।
हल:
| x | ≤ 3

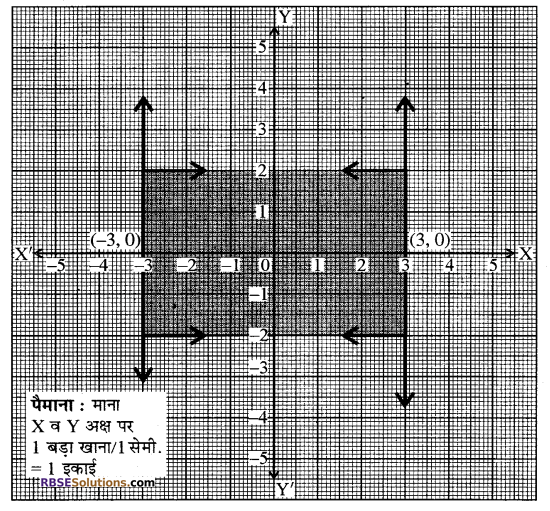
⇒ – 3 ≤ x ≤ 3
⇒ x ≤ 3 तथा x ≥ – 3
असमिका x <3 के संगत समीकरण x = 3 है। (RBSESolutions.com) यह मूल बिन्दु से दायीं ओर 3 इकाई दूरी पर }-अक्ष के समान्तर एक रेखा है। बिन्दु (0, 0) असमिका को सन्तुष्ट करता है। इसलिए मूल बिन्दु हल क्षेत्र में शामिल है।

अतः हल क्षेत्र रेखा x = 3 पर स्थित बिन्दुओं सहित बायीं ओर है। असमिका x ≥ -3 के संगत समीकरण x = – 3 है। यह मूल बिन्दु के बायीं तरफ 3 इकाई दूरी पर y-अक्ष के समान्तर एक रेखा है। बिन्दु (0, 0) असमिका को सन्तुष्ट करता है। इसलिए मूल बिन्दु हल क्षेत्र में शामिल है। अतः हल क्षेत्र रेखा x = – 3 पर स्थित बिन्दुओं सहित दायीं ओर है अतः दी गई असमिका का हल क्षेत्र रेखाओं x = – 3 तथा x = 3 के मध्य का छायांकित भाग है।

प्रश्न 9.
असमिका 2x + 3y ≥ 3 के हल समुच्चय को छायांकित कीजिए।
हल:
सबसे पहले हम दी गयी असमिका के संगत समीकरण को (RBSESolutions.com) लिखने पर

2x + 3y = 3
समीकरण 2x + 3y = 3 का ग्राफ खण्डित रेखा के रूप में खींचा। (RBSESolutions.com) समीकरण में x = 0 तथा y = 0 रखने पर x-अक्ष पर \(B\left( \frac { 3 }{ 2 } ,0 \right) \) तथा x-अक्ष बिन्दु प्राप्त होते हैं। इसका ग्राफ संलग्न आकृति में प्रदर्शित है। अब असमिका में x = (0 तथा y = 0 रखने पर
2x + 3y ≥ 3
2(0) + 3(0) ≥ 3
या 0 ≥ 3 जो कि असत्य है। अतः मूल बिन्दु असमिका 2x + 3y ≥ 3 के क्षेत्र में नहीं है।
अतः अभीष्ट असमिका का हल क्षेत्र मूल बिन्दु के विपरीत, सरल रेखा 2x + 3y = 3 पर स्थित बिन्दुओं उहित होगा।

प्रश्न 10.
निम्न रैखिक समीकरणों के युग्म को आलेखीय विधि से हल – कीजिए तथा इसकी सहायता से ‘a’ का मान ज्ञात कीजिए जबकि 4x +3y = a है। x +3y = 6; 2x – 3y = 12 (माध्य. शिक्षा बोर्ड, मॉडल पेपर, 2017-18 )
हल:
समीकरण x + 3y = 6 द्वारा निरूपित रेखा का आलेखन
दिया है- x + 3y = 6 ⇒ x = 6 – 3y
y = 1 रखने पर x = 6 – 3 x 1 = 6 – 3 = 3
तथा y = 2 रखने पर x = 6 – 3 x 2 = 6 – 6 = 0
अतः समीकरण x + 3y = 6 की निम्न हल सारणी प्राप्त (RBSESolutions.com) होती है-

x	3	0
y	1	2

बिन्दुओं A(3, 1) व B(0, 2) को ग्राफ पेपर पर अंकित करके इनसे गुजरने वाली रेखा AB खींचते हैं जो कि समीकरण x + 3y = 6 का आलेख है।
समीकरण 2x – 3y = 12 द्वारा निरूपित रेखा का आलेखन


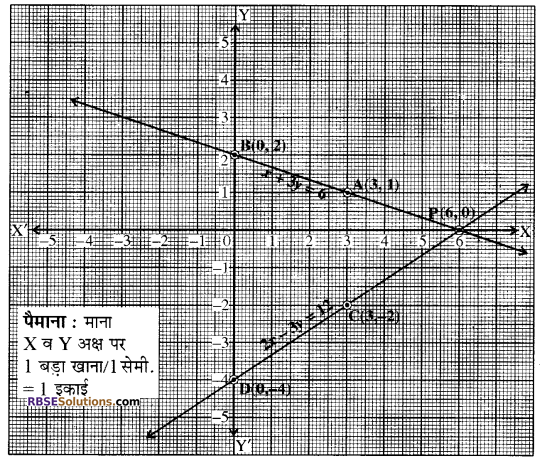
अतः समीकरण 2x – 3y = 12 का निम्न हल सारणी में प्राप्त (RBSESolutions.com) होता है-

x	3	0
y	-2	-4

बिन्दुओं C(3,- 2) तथा D(0, – 4) को उसी ग्राफ पर प्रदर्शित करते हुए उनसे गुजरने वाली रेखा CD खींचते हैं जो कि समीकरण 2x – 3y = 12 का ग्राफ दर्शाती है। ग्राफ से स्पष्ट है कि दोनों समीकरणों के संगत सरल रेखायें एक-दूसरे को बिन्दु P(6, 0) पर काटती हैं।
अत: x = 6 तथा y = 0 दिये गये समीकरण युग्म का हल है।
4x + 3y = a में x = 6 व y = 0 रखने पर
4 x 6 + 3 x 0 = a
⇒ a = 24 उत्तर

प्रश्न 11.
निम्न रैखिक समीकरण युग्म को आलेखिक विधि से हल कीजिए तथा (RBSESolutions.com) उन बिन्दुओं के निर्देशांक ज्ञात कीजिए जहाँ इनके द्वारा निरूपित रेखाएँ y-अक्ष को काटती हैं। 3x + 2y = 12; 5x – 2y = 4
हल:
दिये गये रैखिक समीकरण युग्म हैं-
3x + 2y = 12 ……….(i)
5x – 2y = 4 …..(ii)

अतः समीकरण 3x + 2y= 12 की निम्न हल सारणी (RBSESolutions.com) प्राप्त होती है-

x	2	4
y	3	0

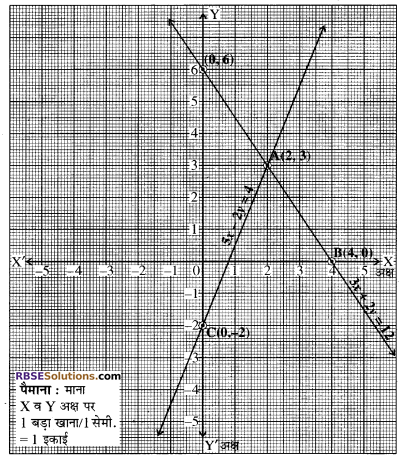
बिन्दुओं A(2, 3) व B(4, 0) को ग्राफ पेपर पर (RBSESolutions.com) अंकित करके इनसे गुजरने वाली रेखा AB खींचते हैं जो कि समीकरण 3x + 2y = 12 का आलेख है।
समीकरण 4x – 2y = 4 द्वारा निरूपित रेखा का आलेखन
5x – 2y = 4

अतः समीकरण 5x – 2y = 4 की निम्न हल सारणी प्राप्त होती है-

x	0	2
y	-2	3

बिन्दुओं C(0, – 2) व A(2, 3) को ग्राफ पेपर पर (RBSESolutions.com) अंकित करके इनसे गुजरने वाली रेखा AC खींचते हैं जो कि समीकरण 5x – 2y = 4 का आलेख है।

ग्राफ से स्पष्ट है कि दोनों समीकरणों के संगत सरल रेखायें एक-दूसरे को बिन्दु A(2, 3) पर काटती हैं। अतः x = 2 तथा y = 3 दिये गये समीकरण युग्म का हल है।
ये दोनों सरल रेखायें -अक्ष को बिन्दु (0, 6) और (0, -2) पर काटती हैं।

अन्य महत्त्वपूर्ण प्रश्न

वस्तुनिष्ठ प्रश्न

प्रश्न 1.
यदि 2x + y = 6 हो तो इसको सन्तुष्ट करने वाला युग्म है
(A) (1, 2)
(B) (2, 1)
(C) (2, 2)
(D) (1, 1)

प्रश्न 2.
यदि \(\frac{4}{x}+5 y=7\) तथा \(x=-\frac{4}{3}\) हो, तो y का (RBSESolutions.com) मान होगा-
(A) \(\frac { 37 }{ 15 } \)
(B) 2
(C) \(\frac { 1 }{ 2 } \)
(D) \(\frac { 1 }{ 3 } \)

प्रश्न 3.
समीकरण \(\frac{y-3}{7}-\frac{x}{2}=1\) में यदि y = 10 हो, तो x बराबर है-
(A) 0
(B) 1
(C) – 2
(D) 2

प्रश्न 4.
यदि रैखिक समीकरणों का कोई युग्म संगत है, तो इसके आलेख की रेखायें होंगी–
(A) समान्तर
(B) सदैव सम्पाती
(C) प्रतिच्छेदी या सम्पाती
(D) सदैव प्रतिच्छेदी

प्रश्न 5.
समीकरण y = 0 और y = – 7 के (RBSESolutions.com) युग्म-
(A) का एक हल है
(B) के दो हल हैं।
(C) अपरिमित रूप से अनेक हल हैं
(D) का कोई हल नहीं है।

प्रश्न 6.
पिता की आयु पुत्र की आयु की तिगुनी है, यदि पिता की आयु x वर्ष है, तो 5 वर्ष बाद पुत्र की आयु होगी|
(A) 3x +5
(B) x +5
(C) \(\frac{x}{3}+5\)
(D) \(\frac{x+5}{3}\)

प्रश्न 7.
x-अक्ष पर बिन्दु है
(A) (2; 3)
(B) (2, 0)
(C) (0, 2)
(D) (2, 2)

प्रश्न 8.
बिन्दु P(3, – 4) जिस चतुर्थाश में है, (RBSESolutions.com) वह है
(A) प्रथम
(B) द्वितीय
(C) तृतीय
(D) चतुर्थ

प्रश्न 9.
एक असमिका का चिह्न-
(A) बदलता है जब हम असमिको के दोनों ओर एक धनात्मक संख्या से गुणा करते हैं।
(B) बदलता है जब असमिका के दोनों ओर एक ऋणात्मक संख्या से गुणा करते हैं।
(C) निश्चित रूप से कुछ नहीं कहा जा सकता है।
(D) इनमें से कोई नहीं।

प्रश्न 10.
असमिका x² + 3x – 2 > 0 का हल है-
(A) (- 1, 2)
(B) (2, 1)
(C) (1, 2)
(D) (2, – 1)

उत्तर-तालिका
1. (C) 2. (B) 3. (A) 4. (C) 5. (D) 6. (C) 7. (B) 8. (D) 9. (B) 10. (C)

अतिलघूत्तरात्मक प्रश्न

प्रश्न 1.
K के किस मान के लिए (RBSESolutions.com) समीकरण निकाय 2x + ky = 1; 3x – 5y = 7 का कोई हल विद्यमान नहीं है?
हल:
कोई हल नहीं होने के लिए।

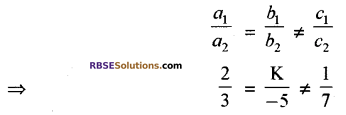
प्रश्न 2.
अनुपातों \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात कीजिये कि रैखिक समीकरणों 2x – 2y – 2 = 0 तथा 4x – 4y – 5 = 0 के युग्म संगत हैं। या असंगत
हल:
समीकरणों 2x – 2y – 2 = 0 तथा 4x – 4y – 5 = 0 की तुलना करने पर

अतः समीकरणों का युग्म संगत है। उत्तर

प्रश्न 3.
दिखाइये रेखाएँ x – 4y + 5 = 0 और 3x – 12y + 8 = 0 समान्तर (RBSESolutions.com) हैं।
हल:
दी गयी रेखाओं के समीकरण
x – 4y + 5 = 0
तया 3x – 12y + 8 = 0
उपर्युक्त समीकरण युग्म की व्यापक समीकरण युग्म से तुलना करने पर
a₁ = 1, b₁ = – 4, c₁ = 5 तथा a₂ = 3, b₂ = – 12, c₂ = 8

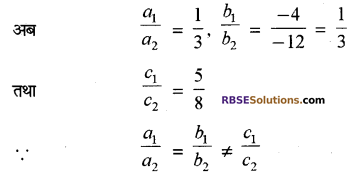
दिये गये समीकरण युग्म असंगत हैं। अतः दी गयी रेखाएँ समान्तर हैं।

प्रश्न 4.
दो चर वाले रैखिक समीकरण युग्म का निरूपण एवं हल प्रस्तुत (RBSESolutions.com) करने की विधियाँ लिखिए।
हल:

1. ग्राफीय विधि,
2. बीजीय विधि

प्रश्न 5.
रैखिक समीकरणों के असंगत युग्म से आप क्या समझते हो?
उत्तर:
यदि दोनों रेखाएँ समान्तर हों, तब इस रैखिक समीकरण युग्म का कोई हल नहीं होता है। इस दशा में यह रैखिक समीकरणों का असंगत युग्म कहलाता है।

प्रश्न 6.
निम्न समीकरण निकाय के हलों की प्रकृति ज्ञात कीजिए-
2x + 4y = 7, 3x + 6y = 10
हल:
2x + 4y – 7 = 0
3x + 6y – 10 = 0
a₁x + b₁x + c = 0 तथा a₂x + b₂y + c₂ = 0 से तुलना करने पर
\(\frac{a_{1}}{a_{2}}=\frac{2}{3}\) तथा \(\frac{b_{1}}{b_{2}}=\frac{4}{6}=\frac{2}{3}\) तथा \(\frac{c_{1}}{c_{2}}=\frac{7}{10}\)
अतः \(\frac{2}{3}=\frac{2}{3} \neq \frac{7}{10}\)
अतः समीकरण निकाय असंगत है और निकाय का कोई हल नहीं है।

प्रश्न 7.
रैखिक समीकरण युग्म 3x + 4y = 0 तथा 2x – y = 0 का हल (RBSESolutions.com) लिखिए।
हल:
x= 0 तथा y = 0 उत्तर

प्रश्न 8.
यदि रैखिक समीकरण a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 में यदि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) हो, तो इस स्थिति का अर्थ स्पष्ट कीजिए।
हल:
यदि \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\) हो, तो रैखिक समीकरण युग्म असंगत है

प्रश्न 9.
समीकरण 5y – 3y – 10 = 0 में y को x के रूप में व्यक्त कीजिए। वह बिन्दु ज्ञात कीजिए जहाँ समीकरण 5y – 3x – 10 = 0 द्वारा निरूपित रेखा y-अक्ष को काटती है।
हल:
समीकरण 5y – 3x – 10 = 0
या 5y = 3x + 10
∴ \(y=\frac{3 x+10}{5}\) उत्तर
समीकरण 5y – 3x – 10 = 0 में रेखा -अक्ष पर तब काटेगी जब x = 0 हो तो \(y=\frac{3 \times 0+10}{5}=2\)
अतः वह बिन्दु (0, 2) होगा। उत्तर

प्रश्न 10.
यदि रैखिक समीकरण a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 में \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) हो, तो इस स्थिति का अर्थ स्पष्ट कीजिए।
हल:
यदि \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) हो, तो रैखिक (RBSESolutions.com) समीकरण युग्म संगत होता है।

प्रश्न 11.
p के किन मानों के लिए, निम्न समीकरणों के युग्म का एक अद्वितीय हल है?
4x + py + 8 = 0
2x + 2y + 2 = 0
हल:
यहाँ a₁ = 4, a₂ = 2, b₁ = p, b₂ = 2 है।
अब दिए गए युग्म का एक अद्वितीय हल होने के लिए, \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) होगा।
अर्थात् \(\frac{4}{2} \neq \frac{p}{2}\)
अर्थात् p ≠ 4
अतः 4 के अतिरिक्त, p के प्रत्येक मान के लिए दिए हुए समीकरण युग्म का एक अद्वितीय हल होगा।

प्रश्न 12.
असमिका क्या है?
उत्तर:
एक गणितीय कथन जिसमें चर एवं (RBSESolutions.com) चिह्न >, <, ≥ या ≤ विद्यमान हो, असमिका कहलाती है।
असमिकायें एक चर वाली या एक से अधिक चर वाली हो सकती हैं।

प्रश्न 13.
एक चर वाली रैखिक असमिकायें किसे कहते हैं?
उत्तर:
माना a एक अशून्य वास्तविक संख्या है तो चर x के लिए ax + b < 0, ax + b ≤ 0, 4x + b > 0 और a + b ≥ 0 असमिकायें एक चर वाली रैखिक असमिकायें कहलाती हैं।

प्रश्न 14.
दो चर वाली रैखिक असमिकायें क्या हैं?
उत्तर:
माना a, b दो अशून्य वास्तविक संख्यायें हैं। x और y चरों के लिए असमिकायें ax + by < c, ax + by ≤ c, ax + by > c या ax + by ≥ c दो चरों वाली रैखिक असमिकायें कहलाती हैं।

प्रश्न 15.
यदि मूल बिन्दु असमिका को सन्तुष्ट नहीं करता है (RBSESolutions.com) तो छायांकित क्षेत्र रेखा के किस तरफ होगा?
उत्तर:
रेखा के मूल बिन्दु की विपरीत होगी यही क्षेत्र असमिका का अभीष्ट हल होगा।

प्रश्न 16.
सरल रेखा ax + by = c, xy-तल को कितने भागों में विभाजित करती है और वे कौन-कौनसे हैं?
उत्तर:
सरल रेखा ax + by = c, xy-तल को दो भागों में विभाजित करती है ये विभाजित क्षेत्र ax+ by ≤ 0 एवं ax + by ≥ c द्वारा व्यक्त किये जा सकते हैं।

लघूत्तरात्मक प्रश्न

प्रश्न 1.
अनुपातों \(\frac{a_{1}}{a_{2}}, \frac{b_{1}}{b_{2}}\) और \(\frac{c_{1}}{c_{2}}\) की तुलना कर ज्ञात (RBSESolutions.com) कीजिए कि निम्न समीकरण युग्म द्वारा निरूपित रेखाएँ एक बिन्दु पर प्रतिच्छेद करती हैं, समान्तर हैं अथवा संपाती हैं-
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
हल:
(i) दी गई रैखिक समीकरण युग्म है-
5x – 4y + 8 = 0
और 7x + 6y – 9 = 0
उक्त समीकरणों की तुलना a₁x + b₁y + c₁ = 0 तथा
a₂x + b₂y + c₂ = 0 से करने पर
यहाँ a₁ = 5, b₁ = – 4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = – 9
अब \(\frac{a_{1}}{a_{2}}=\frac{5}{7} ; \frac{b_{1}}{b_{2}}=\frac{-4}{6}=\frac{-2}{3} ; \frac{c_{1}}{c_{2}}=\frac{8}{-9}\)
\(\therefore \frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)
अतः, दी गई रैखिक समीकरण युग्म एक बिन्दु पर (RBSESolutions.com) प्रतिच्छेदित करती है। उत्तर

(ii) दी गई रैखिक समीकरण युग्म है :
9x + 3y + 12 = 0
और 18x + 6y + 24 = 0
उक्त समीकरणों की तुलना a₁x + b₁y + c₁ = 0 तथा
a₂x + b₂y + c₂ = 0 से करने पर

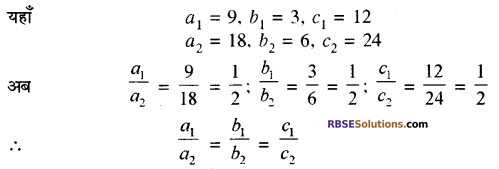
अतः, दी गई समीकरण-युग्म संपाती है। उत्तर

(iii) दी गई रैखिक समीकरण-युग्म है :
6x – 3y + 10 = 0
और 2x – y + 9 = 0
उक्त समीकरणों की (RBSESolutions.com) तुलना a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर

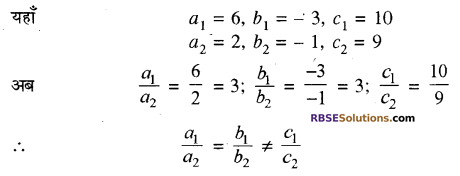
अतः, दी गई रैखिक समीकरण-युग्म एक-दूसरे के समान्तर है। उत्तर

प्रश्न 2.
अनुपातों और की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के युग्म संगत हैं या असंगत
(i) 3x + 2y = 5; 2x – 3y = 7
(ii) \(\frac{3}{2} x+\frac{5}{3} y=7 ; 9 x-10 y=14\)
हल:
(i) दी गई रैखिक समीकरण-युग्म है|
3x + 2y = 5
और 2x – 3y = 7
या 3x + 2y – 5 = 0
और 2x – 3y – 7 = 0
यहाँ a₁ = 3, b₁ = 2, c₁ = – 5
a₂ = 2, b₂ = – 3, c₂ = – 7

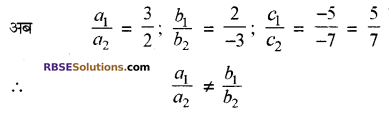
अतः, दी गई रैखिक (RBSESolutions.com) समीकरण-युग्म संगत है। उत्तर

(ii) दी गई रैखिक समीकरण-युग्म है-
\(\frac{3}{2} x+\frac{5}{3} y=7\)
और 9x – 10y = 14

अतः, दी गई रैखिक समीकरण-युग्म संगत है। उत्तर

प्रश्न 3.
नीचे दिये गये निम्न रैखिक समीकरणों (RBSESolutions.com) की जाँच कीजिये कि कौनसे समीकरण युग्म संगत हैं या असंगत
(i) 5x – 3y = 11; – 10x + 6y = – 22
(ii) \(\frac{4}{3} x+2 y=8\) 2x + 3y = 12
हल:
(i) दी गई रैखिक समीकरण-युग्म है-

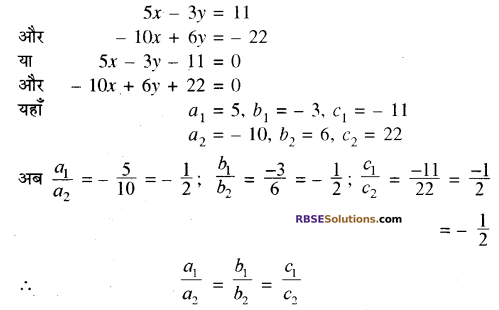
अतः, दी गई रैखिक समीकरण-युग्म संगत और आश्रित है (RBSESolutions.com) और हल असीमित होंगे, सम्पाती रेखायें हैं। उत्तर

(ii) दी गई रैखिक समीकरण-युग्म है-

∴ समीकरण युग्म द्वारा निरूपित रेखाएं सम्पाती होंगी।
अत: रैखिक समीकरण का यह युग्म संगत और आश्रित है। उत्तर

प्रश्न 4.
k के किस मान के लिए, निम्न रैखिक (RBSESolutions.com) समीकरणों के युग्म के अपरिमित रूप से अनेक हल होंगे?
kx + 3y – (k – 3) = 0
12x + ky – k = 0
हल:
यहा \(\frac{a_{1}}{a_{2}}=\frac{k}{12}, \frac{b_{1}}{b_{2}}=\frac{3}{k}, \frac{c_{1}}{c_{2}}=\frac{k-3}{k}\) है।
रैखिक समीकरणों के युग्म के अपरिमित रूप से अनेक हल होने के लिए, \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) होना चाहिए।

जिसमें k² = 36 प्राप्त होता है, अर्थात् k = ± 6 हैं।
साथ ही \(\frac{3}{k}=\frac{k-3}{k}\)
जिससे 3k = k²2 – 3k प्राप्त होता है, अर्थात् 6k = k² है।
जिसका अर्थ k = 0 या k = 6 है।
इसलिए, k का मान, जो दोनों प्रतिबन्धों को सन्तुष्ट करता है, k = 6 है। इस मान के लिए समीकरणों के युग्म के अपरिमित रूप से अनेक हल हैं। उत्तर

प्रश्न 5.
द्विविमीय तल में असमिका 3r – 6 ≥ 0 का (RBSESolutions.com) आलेखन-विधि से हल कीजिए।
हल:

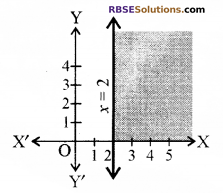
3x – 6 > 0 का आलेख आकृति में दिया गया है।
हम एक बिन्दु (0, 0) का चयन करते हैं और इसे दी गई असमिका में रखने पर हम पाते हैं कि
3 (0) – 6 ≥ 0 या – 6 ≥ 0 जो कि असत्य है।
इस प्रकार दी गई असमिका का हल-क्षेत्र रेखा x = 2 के दाहिनी ओर छायांकित भाग है।

प्रश्न 6.
y <2 को आलेखन विधि से हल कीजिए।
हल:
y = 2 का आलेख दिया गया

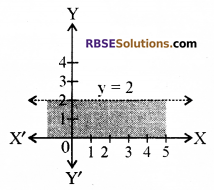
हम निचले अर्द्ध-तल I में एक बिन्दु जैसे (0, 0) का चयन करते हैं और दी गई। (RBSESolutions.com) असमिका में y= 0 रखने पर हम पाते हैं कि 0 < 2 जो कि सत्य है।
इस प्रकार रेखा y= 2 के नीचे का क्षेत्र जिसमें मूल बिन्दु (0, 0) स्थित है, दी गई। असमिका का हल-क्षेत्र है। अत: रेखा y = 2 के नीचे के समस्त बिन्दु (जिसमें रेखा के बिन्दु सम्मिलित नहीं हैं) दी गई असमिका के हल हैं

प्रश्न 7.
असमिका r + y < 5 को हल क्षेत्र आलेखन-विधि से द्विविमीय तल में निरूपित कीजिए।
हल:
सबसे पहले हमने समीकरण x + y = 5 का ग्राफ खण्डित रेखा के रूप में खींचा समीकरण में y = 0 तथा x = 5 रखने पर x-अक्ष पर बिन्दु (5, 0) प्राप्त होता है तथा 1-अक्ष पर बिन्दु (0, 5) इस प्रकार इस समीकरण का ग्राफ आकृति में प्रदर्शित है।

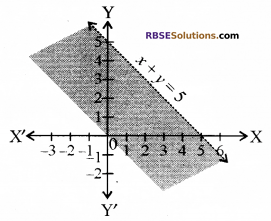
अब असमिका x + y < 5 में x = 0 तथा y = 0 रखने पर 0 + 0 < 5 जो कि सत्य है। अतः मूल बिन्दु x + y < 5 के क्षेत्र में है। इस रेखा पर अन्य कोई बिन्दु असमिका को सन्तुष्ट नहीं करता है। अतः छायांकित क्षेत्र x + y < 5 को निरूपित करता है। यही इस असमिका का हल है।

निबन्धात्मक प्रश्न

प्रश्न 1.
निम्न रैखिक समीकरणों के युग्मों में से (RBSESolutions.com) कौनसे युग्म संगत/ असंगत हैं, यदि संगत हैं तो ग्राफीय विधि से हल ज्ञात कीजिए
(i) x – y = 8, 3x – 3y = 16
(ii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iii) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
हल:
(i) दी गई रैखिक समीकरण-युग्म है-
x – y = 8
और 3x – 3y = 16
था x – y – 8 = 0
और 3x – 3y – 16 = 0
उक्त समीकरण युग्म की तुलना समीकरण युग्म a₁x + b₁y + c₁ = 0 तथा a₂x + b₂y + c₂ = 0 से करने पर

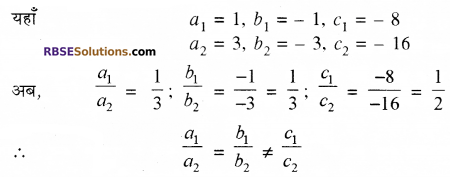
दिये गये समीकरण युग्म का कोई हल नहीं होगा।
अतः, दी गई रैखिक समीकरण-युग्म असंगत है। उत्तर

(ii) दी गई रैखिक (RBSESolutions.com) समीकरण-युग्म है-
2x + y – 6 = 0
और 4x – 2y – 4 = 0
यहाँ a₁ = 2, b₁ = 1, c₁ = – 6

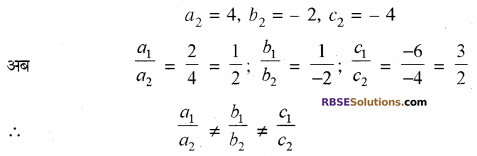
दिये गये समीकरण युग्म का एक अद्वितीय हल होगा।
∴ दी गई रैखिक समीकरण-युग्म संगत है।
इन रैखिक समीकरणों का आलेख खींचने पर
2x + y – 6 = 0
या y = 6 – 2x
x = 1 रखने पर तब y = 6 – 2 × 1 = 6 – 2= 4
x = 2 रखने पर तब y = 6 – 2 × 2 = 6 – 4 = 2
अतः सारणी प्राप्त होती है-

x	1	2
y	4	2

बिन्दुओं A(1, 4), B(2, 2) को आलेखित करने (RBSESolutions.com) और उनको मिलाते हुए रेखा खींचने पर हमें समीकरण 2x + y – 6 = 0 आलेख प्राप्त होता है। पुनः दूसरा रैखिक समीकरण लेने पर
4x – 2y – 4 = 0
या 2[2x – y – 2]= 0
या 2x – y – 2= 0
या y = 2x – 2
x = 1 रखने पर तब y = 2 × 1 – 2 = 2 – 2 = 0
x = 2 रखने पर तब y = 2 × 2 – 2 = 4 – 2 = 2
अतः सारणी प्राप्त होती है-

x	1	2
y	0	2

बिन्दुओं C(1, 0), B(2, 2) को आलेखित करने पर और उनको मिलाते हुए खींचने पर हमें समीकरण 4x – 2y – 4 = 0 का आलेख प्राप्त होता है।
आलेख से स्पष्ट है कि दी गई समीकरण (RBSESolutions.com) युग्म बिन्दु B(2, 2) पर मिलती है।

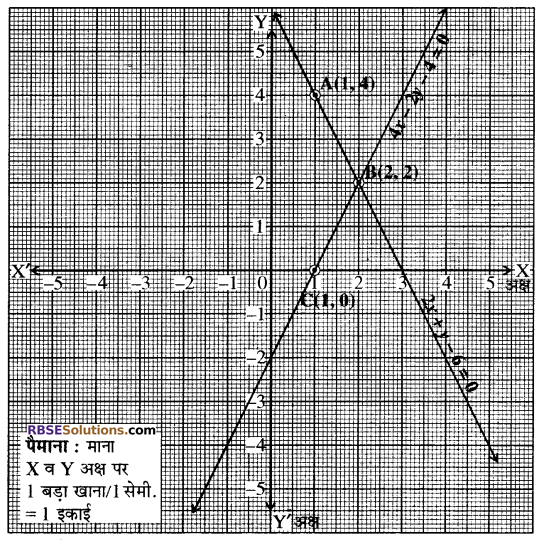
अतः दी गई रैखिक समीकरण-युग्म अद्वितीय है। उत्तर

(iii) दी गई रैखिक (RBSESolutions.com) किरण-युग्म है-
2x – 2y – 2 = 0
और 4x – 4y – 5 = 0
यहाँ a₁ = 2, b₁ = – 2, c₁ = – 2
a₂ = 4, b₂ = – 4, c₂ = – 5

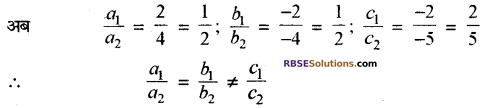
∴ दिये गये समीकरण युग्म का कोई हल नहीं है। अतः, दी गई समीकरण युग्म असंगत है। उत्तर

प्रश्न 2.
आलेखीय विधि द्वारा अग्र समीकरण (RBSESolutions.com) निकाय का हल ज्ञात कीजिए-
2x + 3y = 13
5x- 2y = 4
हल:
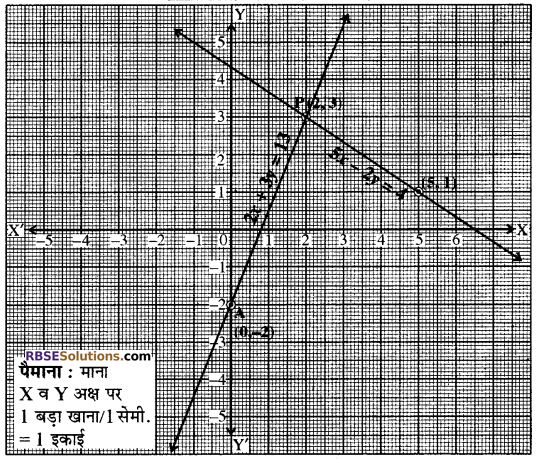
दिये गये समीकरण निकाय हैं-
2x + 3 = 13 ………(i)
5x – 2y = 4 ………..(ii)
समीकरण (1) में x = 2 रखने पर
2 × 2 + 3y = 13
⇒ 4 + 3y = 13
या 3y = 13 – 4 = 9
\(y=\frac{9}{3}=3\)
अब x = 5 रखने पर
2 × 5 + 3y = 13
या 10 + 3y = 13
या 3y = 13 – 10 = 3
या \(y=\frac{3}{3}=1\)
अतः बिन्दु निम्न सारणी अनुसार (RBSESolutions.com) प्राप्त हुए हैं-

x	2	5
y	3	1

इसी प्रकार (RBSESolutions.com) समीकरण (2) में x = 0 रखने पर
5 × 0 – 2y = 4
⇒ 0 – 2y = 4
या – 2y = 4
या \(y=\frac{4}{-2}=-2\)
समीकरण (2) में x = 2 रखने पर
5 × 2 – 2y = 4
या 10 – 2y = 4
या – 2y = 4 – 10 = – 6
∴ y = 3
अतः बिन्दु निम्न सारणी अनुसार प्राप्त हुए हैं-

x	0	2
y	-2	3

अब हम उपरोक्त सारणियों से प्राप्त बिन्दुओं को ग्राफ पेपर पर निरूपित कर निम्न सरल रेखायें प्राप्त करते हैं अर्थात् ग्राफ पेपर पर XOX’ तथा YOY’ अक्षों का निर्माण कर सारणी में दिये गये बिन्दुओं को मिलाकर सरल रेखा प्राप्त करते हैं।

दोनों सरल रेखायें बिन्दु P(2, 3) पर प्रतिच्छेद होती हैं। (RBSESolutions.com) अतः समीकरण निकाय का हल x = 2, y = 3 है। उत्तर,

प्रश्न 3.
आलेखीय विधि द्वारा निम्न समीकरण निकाय का हल ज्ञात कीजिए
2x + 4y = 10
3x + 6y = 12
हल:
दिये गये समीकरण निकाय हैं-
2x + 4y = 10
3x + 6y = 12
समीकरण (1) से
2x + 4y = 10
या 4y = 10 – 2x

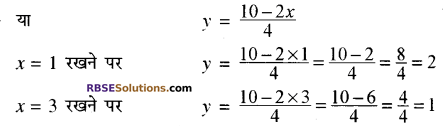
अतः समीकरण (1) के लिए बिन्दु सारणी (RBSESolutions.com) निम्न प्रकार प्राप्त होती है-

x	1	3
y	2	1

इसी प्रकार समीकरण (2) से
3x = 6y = 12
या 6y = 12 – 3x

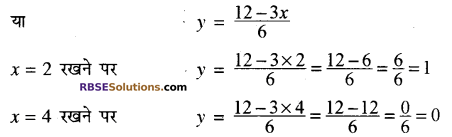
अतः समीकरण (2) के लिए बिन्दु (RBSESolutions.com) सारणी निम्न प्रकार प्राप्त होती है-

x	2	4
y	1	0

अब उपरोक्त सारणियों से प्राप्त बिन्दुओं को ग्राफ पेपर पर आलेखित करते हैं एवं बिन्दुओं को मिलाकर ग्राफ (आलेख) प्राप्त करते हैं।
समीकरण निकाय का कोई हल नहीं होगा एवं युग्म असंगत होगा। समान्तर रेखायें होंगी । उत्तर

प्रश्न 4.
निम्न समीकरणों का आलेख विधि से हल ज्ञात कीजिए
4x + 6y = 18
2r + 3y = 9
हल:
दिये गये समीकरण निकाय हैं
4x + 6y = 18 ……….(i)
2x + 3y = 9 …………(ii)
समीकरण (1) में x = 0 रखने (RBSESolutions.com) पर
4 × 0 + 6y = 18
या 0 + 6y = 18
या 6y = 18 या y = 3
x = 3 रखने पर
4 × 3 + 6y = 18
⇒ 12 + 6y = 18
⇒ 6y = 18 – 12 = 6

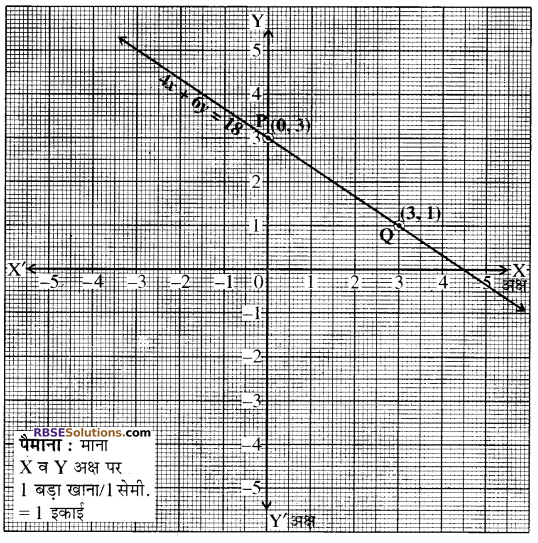
\(y=\frac{6}{6}=1\)
अतः बिन्दु सारणी निम्न प्रकार प्राप्त (RBSESolutions.com) होती है-

x	0	3
y	3	1

समीकरण (2) के लिए x = 0 पर
2 × 0 + 3y = 9
या 0 + 3y = 9
या 3y = 9
∴ \(y=\frac{9}{3}=3\)
तथा x = 3 पर
2 × 3 + 3y = 9
या 6 + 3y = 9
या 3y = 9 – 6 = 3
∴ \(y=\frac{3}{3}=1\)
इस प्रकार समीकरण (2) के लिए सारणी (RBSESolutions.com) प्राप्त हुई-

x	0	3
y	3	1

अब उपरोक्त सारणियों से प्राप्त बिन्दुओं का ग्राफ पेपर पर आलेखन करते हैं। एवं इस प्रकार प्राप्त रेखाओं का ग्राफ आलेख प्राप्त करते हैं।
उपरोक्त ग्राफ (आलेख) में दोनों रेखायें एक-दूसरे को ढके हुए हैं अर्थात् दोनों रेखायें सम्पाती हैं। स्पष्ट है दोनों समीकरण तुल्य रेखाओं को प्रदर्शित करते हैं। उत्तर

प्रश्न 5.
निम्न रैखिक समीकरण युग्मों को आलेखीय विधि से हल कीजिए-
(i) 3x + 2y – 11 = 0
2x – 3y + 10 = 0
(ii) 2x + 3y = 8
x – 2y = – 3
हल:
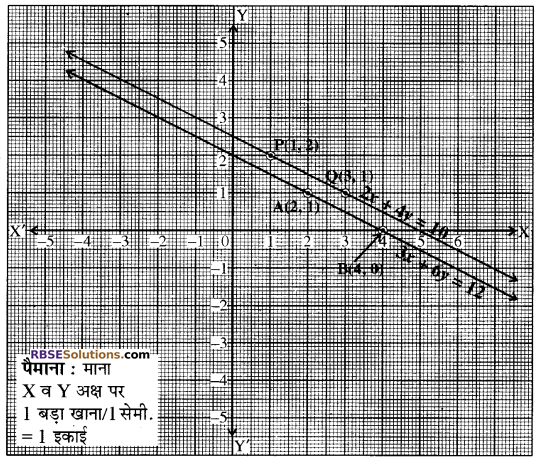
(i) दिया गया रैखिक (RBSESolutions.com) समीकरण युग्म है-
3x + 2y – 11 = 0
या 3x + 2 = 11 …..(1)
2x – 3y + 10 = 0
या 2x – 3y = – 10 …..(2)
संजीव पास बुक्स समीकरण (1) से बिन्दु सारणी प्राप्त करने पर
3x + 2y = 11
2y = 11 – 3x

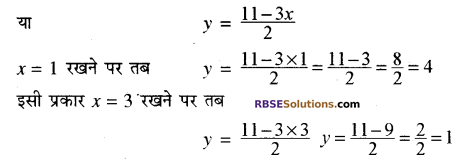
अत: समीकरण (1) की बिन्दु सारणी निम्न प्रकार प्राप्त होती है-

x	1	3
y	4	1

अब समीकरण (2) की बिन्दु सारणी (RBSESolutions.com) प्राप्त करने पर-

x	1	-2
y	4	2

उपरोक्त दोनों समीकरणों से संगत रेखाओं का ग्राफ पेपर पर आलेखन करते हैं।
उपरोक्त निरूपण से स्पष्ट है (RBSESolutions.com) कि दोनों रेखायें बिन्दु (1, 4) पर प्रतिच्छेद करती हैं। अतः x = 1 एवं y = 4 रेखायुग्म 3x + 2y = 11, 2x – 3y = – 10 का अभीष्ट हल है। अर्थात् x = 1, y = 4 मान इन दोनों समीकरणों को सन्तुष्ट करते हैं। अतः हल सत्यापित होता है। उत्तर

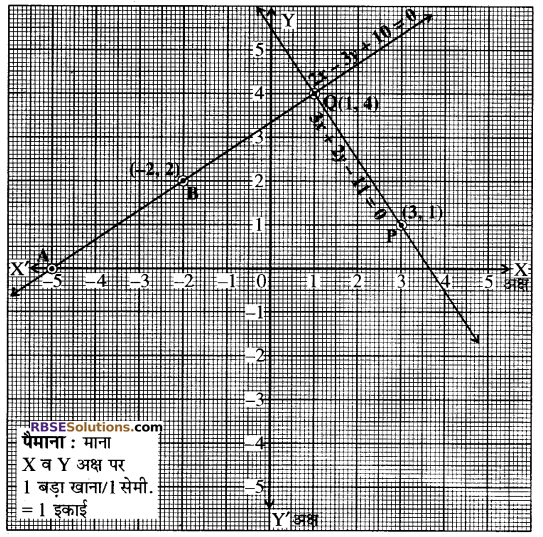
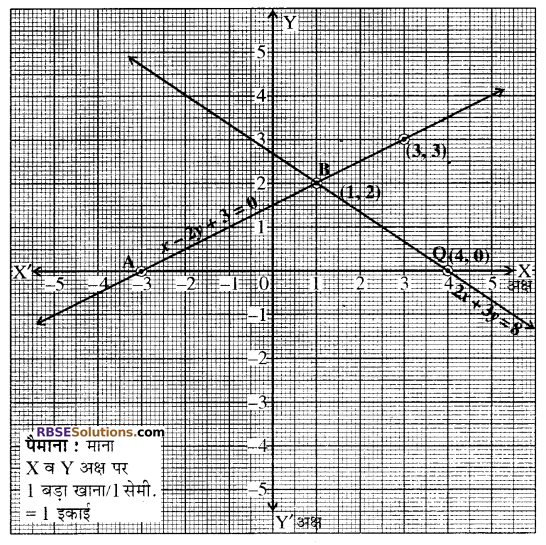
(ii) दिया गया समीकरण युग्म है-
2x + 3y = 8 …….(1)
x – 2y = – 3 …..(2)
हम समीकरण (1) की बिन्दु (RBSESolutions.com) सारणी प्राप्त करने पर-
x = 1 रखने पर
2 × 1 + 3y = 8
या 2 + 3y = 8
या 3y = 8 – 2 = 6
∴ \(y=\frac{6}{3}=2\)
x = 4 रखने पर
2 × 4 + 3y = 8
या 8 + 3y = 8
या 3y = 8 – 8 = 0
∴ \(y=\frac{0}{3}=0\)
अतः समीकरण (1) की बिन्दु सारणी निम्न प्राप्त होती है-

x	1	4
y	2	0

अब हम समीकरण (2) की बिन्दु (RBSESolutions.com) सारणी प्राप्त करते हैं।


इस प्रकार निम्न बिन्दु सारणी (RBSESolutions.com) समीकरण (2) के लिए प्राप्त होती है-

x	1	3
y	2	3

उपरोक्त समीकरण (1) तथा (2) के संगत सारणियों की सहायता से ग्राफ पेपर पर रेखाओं को निरूपित करते हैं।
दोनों रेखायें बिन्दु B(1, 2) पर प्रतिच्छेद होती हैं। अतः समीकरण युग्म का अभीष्ट हल x = 1 व y = 2 है। उत्तर

प्रश्न 6.
निम्न रैखिक समीकरण युग्म को आलेखीय विधिद्वाराहल कीजिए 2x + y = 6, 2x – y = 2 अतः इसकी सहायता से सम्बन्ध 6x + 7y = p में p का मान ज्ञात कीजिए। (माध्य. शिक्षा बोर्ड, 2018)
हल:
दिये गये रैखिक समीकरण युग्म
2x + y = 6 …..(1)
2x – y = 2 …………(2)
समीकरण (1) के संगत बिन्दु सारणी (RBSESolutions.com) प्राप्त करने पर

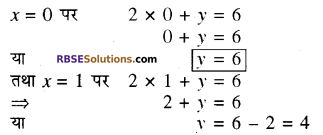
इस प्रकारे समीकरण (1) की बिन्दु सारणी निम्न प्रकार प्राप्त होगी-

x	0	1
y	6	4

अतः समीकरण (2) के संगत बिन्दु (RBSESolutions.com) सारणी प्राप्त करते हैं।
समीकरण (2) में x = 0 रखने पर

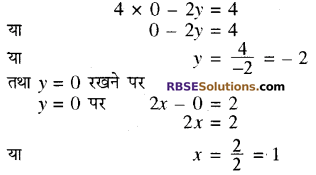
अतः समीकरण (2) की बिन्दु सारणी निम्न प्रकार प्राप्त होती है-

x	0	1
y	-2	0

उपरोक्त समीकरण (1) एवं (2) से प्राप्त बिन्दु सारणियों की सहायता (RBSESolutions.com) से ग्राफ पेपर पर रेखायुग्म का निरूपण करते हैं ।
दोनों रेखायें बिन्दु M(2, 2) पर प्रतिच्छेद करती हैं। अतः समीकरण निकाय का अभीष्ट हल x = 2 व y = 2 है। उत्तर
x = 2 व y = 2 को दिये गये सम्बन्ध 6x + 7y = p में रखने पर
6 × 2 + 7 × 2 = p
⇒ 12 + 14 = p
∴ p = 26 उत्तर

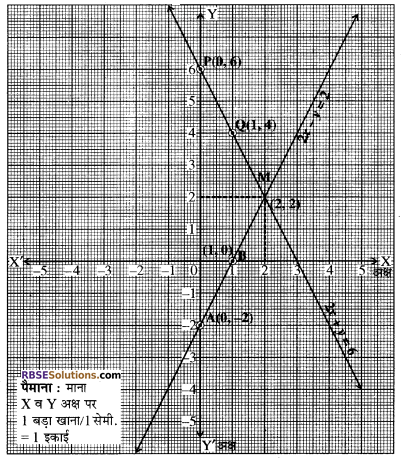
प्रश्न 7.
रैखिक समीकरणों x – y + 1 = 0 और 3x + 2y – 12 = 0 का ग्राफ (RBSESolutions.com) खींचिये।-अक्ष और इन रेखाओं से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिये और त्रिभुजाकार पटल को छायांकित कीजिए।
हल:
रैखिक समीकरण युग्म लेने पर
x – y + 1 = 0
और 3x + 2y – 12 = 0
x – y + 1 = 0
या y = x +1
x = 1 रखने पर तब y = 1 + 1 = 2
x = 2 रखने पर तब y = 2 + 1 = 3
अतः सारणी प्राप्त होती है-

x	2	2
y	2	3

बिन्दु A(1, 2), B(2, 3) को आलेखित करने और उनको मिलाकर (RBSESolutions.com) रेखा खींचने पर हमें समीकरण x – y + 1 = (0 का आलेख प्राप्त होता है।
पुन: दूसरे समीकरण से
3x + 2 – 12 = 0



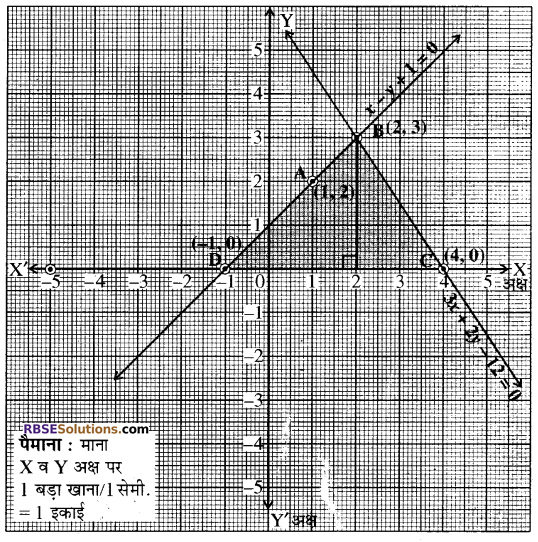
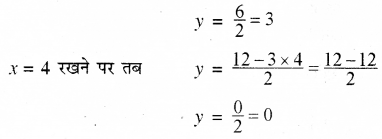
अतः सारणी प्राप्त (RBSESolutions.com) होती है-

x	2	4
y	3	0

बिन्दुओं B(2, 3), C(4, 0) को आलेखित करने पर और उनको मिलाकर रेखा खींचने पर हमें समीकरण 3x + 2y – 12 = 0 का आलेख प्राप्त होता है। रैखिक समीकरणों के युग्म और ४-अक्ष द्वारा बनाये गये त्रिभुज के शीर्षों को आलेख में छायांकित किया गया है। ABCD इस प्रकार बना त्रिभुज है।

∆BCD के शीर्षों के निर्देशांक हैं-
B(2, 3), C(4,0), D(-1, 0) उत्तर

प्रश्न 8.
निम्न असमिकाओं को आलेखन विधि से हल (RBSESolutions.com) कीजिए-
(i) x ≤ 2
(ii) 2x – y ≥ 1
(iii) |y – x | ≤ 3
हल:
(i) दी गयी असमिका है-

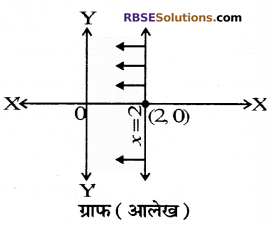
x ≤ 2
इसके संगत समीकरण लिखने पर
x=2
स्पष्ट है यह सरल रेखा y- . अक्ष के समान्तर है एवं -अक्ष के बिन्दु (2, 0) से गुजरेगी। इसका ग्राफ (आलेख) सामने चित्र के ग्राफ ( आलेख) अनुरूप प्राप्त होता है।
अब मूल बिन्दु (0, 0) से असमिका x ≤ 2 सन्तुष्ट होती है अतः क्षेत्र रेखा x = 2 से मूल बिन्दु की ओर छायांकित क्षेत्र ही इसका हल समुच्चय होगा।
(ii) दी गयी असमिका को (RBSESolutions.com) स पीकरण रूप में बदलने पर 2x – y = 1 प्राप्त होता है।
इस समीकरण में x = 0 रखने पर ,
2 × 0 – y = 1

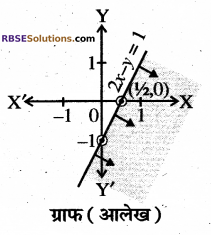
या y = -1 प्राप्त होता है। अतः y-अक्ष पर बिन्दु (0, – 1) कटान बिन्दु है। इसी प्रकार समीकरण में y = 0 रखने पर, \(x=\frac{1}{2}\) प्राप्त होता है। अतः x-अक्ष पर बिन्दु \(\left(\frac{1}{2}, 0\right)\) कटान बिन्दु प्राप्त हुआ। दोनों कटान बिन्दु (0, – 1). एवं \(\left(\frac{1}{2}, 0\right)\) को मिलाने पर इसका ग्राफ आलेख ग्राफ (आलेख) चित्र प्राप्त होता है।

अब मूल बिन्दु (0, 0) से असमिका 2x – y > 1 सन्तुष्ट नहीं होती अर्थात् 2 × 0 – 0 ≥ 1 सत्य नहीं है। अतः रेखा 2x – y = 1 से मूल बिन्दु. के विपरीत छायांकित क्षेत्र ही इसका हल समुच्चय होगा।

(iii) दी गई असमिका | y – x | ≤ 3 है। इस मोड्यूलस को (RBSESolutions.com) हटाने पर निम्नानुसार लिखा जा सकता है
– 3 ≤ y – x ≤ 3
इसे पुनः निम्नानुसार दो असमिकाओं के रूप में लिखा जा सकता है|
– 3 ≤ y – x
तथा y – x ≤ 3
अर्थात् x – y – 3 ≤ 0 …..(i)
तथा x – y + 3 ≥ 0
असमिका (i) को समीकरण रूप में लिखने पर x – y – 3 = 0 प्राप्त होता है।
इसके x-अक्ष पर कटान बिन्दु (3, 0) एवं y-अक्ष पर कटान बिन्दु (0, – 3) प्राप्त होते हैं। इसी प्रकार द्वितीय (ii) असमिका को समीकरण रूप में लिखने पर x – y + 3 = 0 प्राप्त होता है।

इस रेखा के x-अक्ष पर कटान बिन्दु (-3, 0) एवं y-अक्ष पर कटान बिन्दु (0, 3) प्राप्त होते हैं। अब इन दोनों रेखाओं के ग्राफ (आलेख) आगे दर्शाये अनुसार प्राप्त होते हैं।
अब मूल बिन्दु (0, 0) से असमिका x -y – 3 ≤ 0 व x – y + 3 ≥ 0 सन्तुष्ट होती है।
अर्थात् 0 – 0 – 3 ≤ 0 और
0 – 0 + 3 ≤ 0
अतः रेखा x – y – 3 = 0 तथा x – y + 3 = 0 से मूल बिन्दु की (RBSESolutions.com) ओर छायांकित क्षेत्र ही इसका हल समुच्चय होगा।

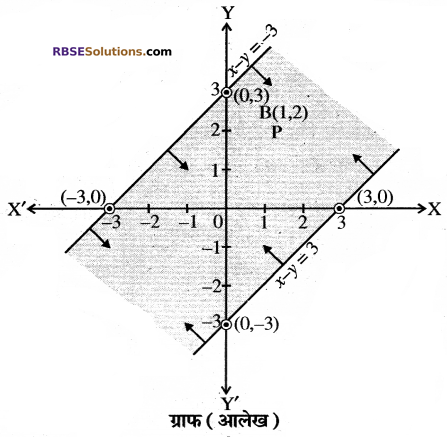
प्रश्न 9.
निम्नलिखित असमिकाओं का हल क्षेत्र (RBSESolutions.com) ज्ञात कीजिए
(i) y > 2
(ii) x < 3 (iii) y ≤ – 1 (iv) x + 2y ≥ 1 हुल: (i) y > 2

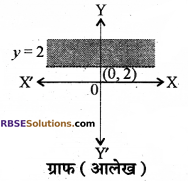
y > 2 असमिका के संगत रेखा y = 2 जो कि x-अक्ष के समान्तर है। असमिको को (0, 0) सन्तुष्ट नहीं करता है। अतः हल क्षेत्र मूल बिन्दु के विपरीत दिशा में होगा और रेखा y = 2 पर स्थित सभी बिन्दु इसमें शामिल नहीं हैं।

(ii) x < 3

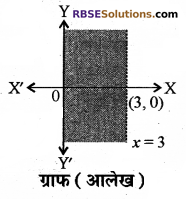
x < 3 असमिका का संगत समीकरण x = 3 है तथा (RBSESolutions.com) असमिका (0, 0) को सन्तुष्ट करती है। अतः हल क्षेत्र रेखा के बायीं ओर होगा और रेखा x = 3 पर स्थित सभी बिन्दु इसमें शामिल नहीं हैं।

(iii) y ≤ – 1

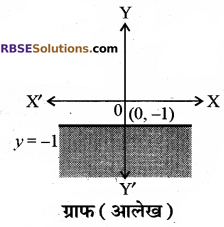
असमिका y ≤ – 1 का संगत समीकरण y = – 1 है तथा असमिका (0, 0) को सन्तुष्ट नहीं करती है। अतः हल क्षेत्र रेखा के नीचे की ओर होगा और रेखा y = -1 पर स्थित सभी बिन्दु रेखा में शामिल हैं।

(iv) x + 2y ≥ 1

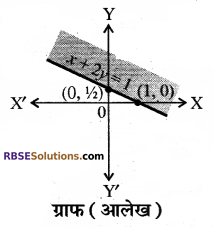
असमिका x + 2y ≥ 1 के संगत (RBSESolutions.com) समीकरण x + 2y = 1 हैं। सबसे पहले हमने समीकरण x + 2y = 1 का ग्राफ खण्डित रेखा के रूप में खींचा। समीकरण में y = 0 तथा x = 0 रखने पर x-अक्ष पर बिन्दु (1, 0) प्राप्त होता है तथा y-अक्ष पर बिन्दु \(\left(0, \frac{1}{2}\right)\) प्राप्त होता है। इस प्रकार इस समीकरण का ग्राफ (आलेख) ग्राफ (आलेख) आकृति में प्रदर्शित है। अब असमिका x + 2y ≥ 1 में x= 0 तथा y= 0 रखने पर।
0 + 2.0 ≥ 1 अर्थात् 0 ≥ 1 जो कि असत्य है।
अतः असमिका का क्षेत्र मूल बिन्दु से विपरीत दिशा में होगा और x + 2y = 1 पर स्थित सभी बिन्दु इसमें शामिल हैं।

We hope the RBSE Solutions for Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Additional Questions, drop a comment below and we will get back to you at the earliest.