RBSE Solutions for Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Ex 4.1 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Exercise 4.1.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 4 |
| Chapter Name | दो चरों वाले रैखिक समीकरण एवं असमिकाएँ |
| Exercise | Exercise 4.1 |
| Number of Questions Solved | 4 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Ex 4.1
प्रश्न 1.
अनुपातों \(\frac { { a }_{ 1 } }{ { a }_{ 2 } } ,\frac { { b }_{ 1 } }{ { b }_{ 2 } } \) और \(\frac { { c }_{ 1 } }{ { c }_{ 2 } } \) की तुलना कर ज्ञात कीजिए कि निम्न रैखिक समीकरणों के (RBSESolutions.com) युग्म संगत हैं या असंगत।
(i) 2r – 3y = 8; 4c – 6y = 9
(ii) 3x – y = 2; 6x – 2y = 4
(iii) 2x – 2y = 2; 4x – 4y = 5
(iv) \(\frac { 4 }{ 3 } \) + 2y = 8; 2x + 3y = 12
हल:
(i) दिया गया रैखिक समीकरण-युग्म है-
23 – 3y = 8 या 2x – 3y – 8 = 0
4x – 6y = 9 या 4x – 6y – 9 = 0
यहाँ a1 = 2, b1 = – 3, c1 = – 8 और a2 = 4, b2 = – 6, c2 = – 9.
\(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { 2 }{ 4 } =\frac { 1 }{ 2 } ,\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { -3 }{ -6 } =\frac { 1 }{ 2 } ,\frac { { c }_{ 1 } }{ { c }_{ 2 } } =\frac { -8 }{ -9 } =\frac { 8 }{ 9 } \)
इस प्रकार से ह\(\frac { 1 }{ 2 } =\frac { 1 }{ 2 } \neq \frac { 8 }{ 9 } \)
अर्थात् \(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } \neq \frac { { c }_{ 1 } }{ { c2 }_{ } } \)
∴ दिये गये समीकरण युग्म का कोई हल नहीं है।
अतः रैखिक समीकरणों का यह युग्म असंगत है। उत्तर
![]()
(ii) दिया गया रैखिक समीकरण-युग्म है-
3x – y = 2 या 3x – y – 2 = 0
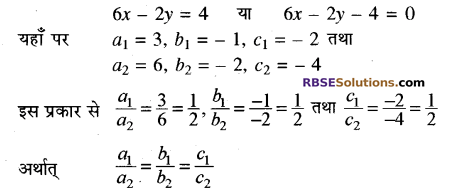
समीकरण युग्म सम्पाती हैं। इसलिये समीकरणं युग्म के अनन्त हल हैं। (RBSESolutions.com) अतः रैखिक समीकरणों का यह युग्म संगत है। उत्तर
(iii) दिया गया रैखिक समीकरण युग्म है-
2x – 2y = 2 या 2x – 2y – 2 = 0
4x – 4y = 5 या 4x – 4y – 5 = 0
यहाँ a1 = 2, b1 = – 2, c1 = – 2 तथा
a2 = 4, b2 = – 4, c2 = -5
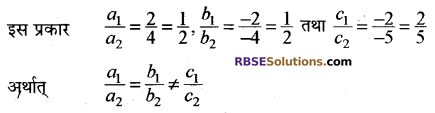
दिये गये समीकरण युग्म का कोई हल नहीं है।
अतः रैखिक समीकरणों का यह युग्म असंगत है। उत्तर
(iv) दिया गया रैखिक समीकरण युग्म है-

दिये गये समीकरण युग्म के अनन्त हल हैं। (RBSESolutions.com) अतः रैखिक समीकरणों का यह युग्म संगत होगा। उत्तर
![]()
प्रश्न 2.
निम्न रैखिक समीकरणों के युग्म को ग्राफीय विधि से हल कीजिए एवं हल की प्रकृति बताइए-
(i) x + y = 3; 3x – 2y = 4
(ii) 2x – y = 4; x + y = -1
(iii) x + y = 5; 2x + 2y = 10
(iv) 3x + y = 2; 2x – 3y = 5
हल:
(i) x + y = 3 के ग्राफ के लिए हमें प्राप्त है-
x + y = 3 या y = 3 – c
यदि x = 0 हो, तो y = 3 तथा यदि x = 3 है, तो y = 0 है। (RBSESolutions.com) अतः हमें तालिका प्राप्त होती है-
| x | 0 | 3 |
| y | 3 | 0 |
अब ग्राफ 3x – 2y = 4
या 2y = 3x – 4
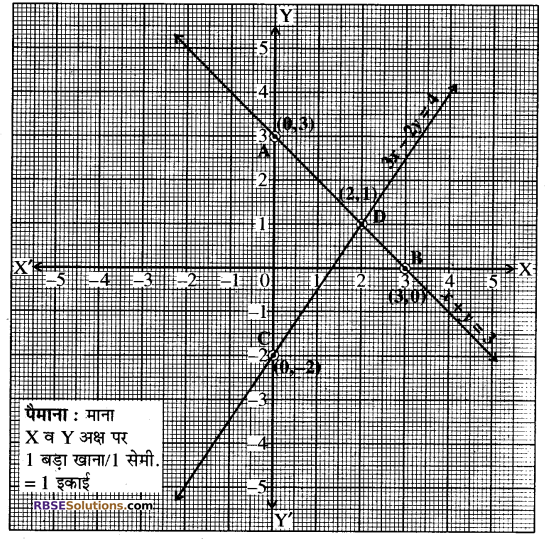
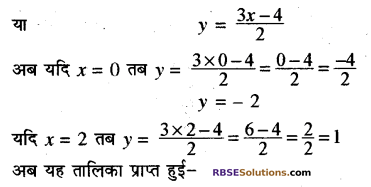
| x | 0 | 2 |
| y | -2 | 1 |
(ii) रैखिक समीकरण युग्म है-बिन्दुओं A(o, 3) तथा B(3, o) को ग्राफ पर (RBSESolutions.com) आलेखित किया गया और इन्हें मिलाकर x + y = 3 का ग्राफ प्राप्त किया गया। अब बिन्दु C(0, -2) और D(2, 1) को ग्राफ पेपर पर आलेखित किया गया और इन्हें मिलाकर 3x – 2 = 4 का ग्राफ आलेखित किया गया ये दोनों रेखायें बिन्दु (2, 1) पर प्रतिच्छेद करती हैं, अतः x = 2 तथा y = 1 ही इनका अभीष्ट हल है।
इस प्रकार दोनों रेखाओं के हल की प्रकृति अद्वितीय हल होगी।
2x – y = 4, x + y = – 1
पहले रैखिक समीकरण से सारणी तैयार करने पर,
2x – y = 4
या 2x – 4 = y
या y = 2x – 4
अब यदि x = 1 तब y= 2 × 1 – 4 = 2 – 4 = -2
यदि x = 0 तब y = 2 × 0 – 4 = 0 – 4 = -4
अतः सारणी-
| x | 1 | 0 |
| y | -2 | -4 |
बिन्दुओं A(1, – 2) तथा B(0, – 4) को ग्राफ पर आलेखित किया गया और इन्हें मिलाकर 2x – y = 4 का ग्राफ (RBSESolutions.com) प्राप्त किया गया।
दूसरे समीकरण से-
x + y = – 1
y = – 1 – x
और यदि x = 1 तब y = -1 – 1 = -2
और यदि x = 2 तब y = – 1 – 2 = – 3
अतः सारणी-
| x | 1 | 2 |
| y | -2 | -3 |
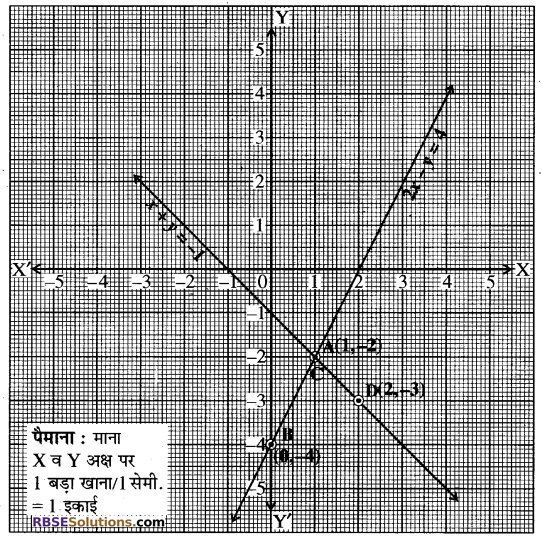
अब बिन्दु A(1, – 2) तथा D(2, – 3) को इसी ग्राफ पर आलेखित कर और इनको मिलाकर x + y =-1 का ग्राफ प्राप्त किया गया।
अब बिन्दु C(1, – 2) और D(2,- 3) को ग्राफ (RBSESolutions.com) पेपर पर आलेखित किया। गया और इन्हें मिलाकर x + y = – 1 का ग्राफ आलेखिंत किया गया। ये दोनों रेखायें बिन्दु C(1, – 2) पर प्रतिच्छेद करती हैं। अतः x = 1, y = – 2 ही इनका हल है। इस प्रकार दोनों रेखाओं के हल की प्रकृति अद्वितीय हल होगी।
हल–(iii) x + y = 5 के ग्राफ के लिए हमें प्राप्त है-
x + y = 5 या y = 5 – x
यदि x = 0 हो, तो y = 5 तथा यदि x = 5 है, तो y = 0 है।
अब, यह तालिका प्राप्त हुई-
| x | 0 | 5 |
| y | 5 | 0 |
अब ग्राफ 2x + 2y = 10 के लिए हमें प्राप्त है-
2x + 2y = 10 या 2 = 10 – 2x
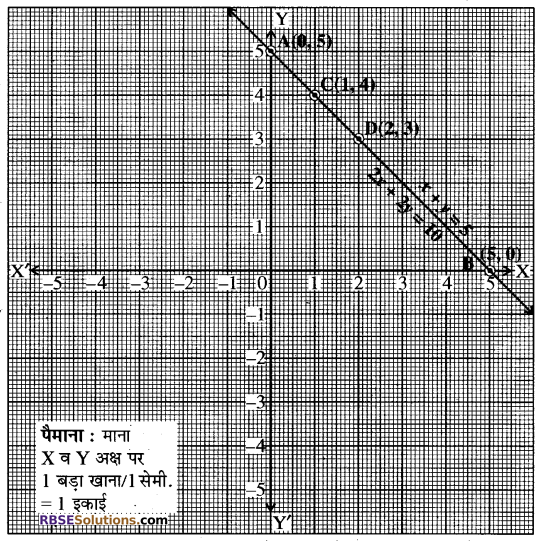
अब, यदि x = 1 हो, तो y = 5 – 1 = 4 है तथा (RBSESolutions.com) यदि x = 2 है, तो y = 5 – 2 = 3 है।
अब यह तालिका प्राप्त हुई-
| x | 1 | 2 |
| y | 4 | 3 |
बिन्दुओं A(0, 5) तथा B(5, 0) को ग्राफ पर आलेखित किया गया और इन्हें मिलाकर x + y = 5 का ग्राफ प्राप्त किया गया। अब C(1, 4) तथा D(2, 3) को इसी ग्राफ पर आलेखित कर और इनको मिलाकर 2x + 2y = 10 का ग्राफ प्राप्त किया गया
हमने देखा कि बिन्दुओं C तथा D, x + 1 = 5 के ही ग्राफ पर स्थित हैं। अतः एक समीकरण का हल दूसरी समीकरण का भी हल है। इस प्रकार इस रैखिक. युग्म के अपरिमित रूप से अनेक हल हैं। अर्थात् अनन्त हल हैं अतः यह रैखिक समीकरण युग्म संगत और आश्रित हैं।
![]()
(iv) दिया गया रैखिक समीकरण युग्म है-
3x + y = 2
2x – 3y = 5
रैखिक समीकरण 3x + y = 2 से
या y = 2 – 3x
यदि x = 0 हो, तो y = 2 – 3 x 0 = 2 – 0 = 2
तथा यदि x = 1 हो, तो y = 2 – 3 x 1 = 2 – 3 = – ।
अतः हमें तालिका प्राप्त होती है-
| x | 0 | 1 |
| y | 2 | -1 |
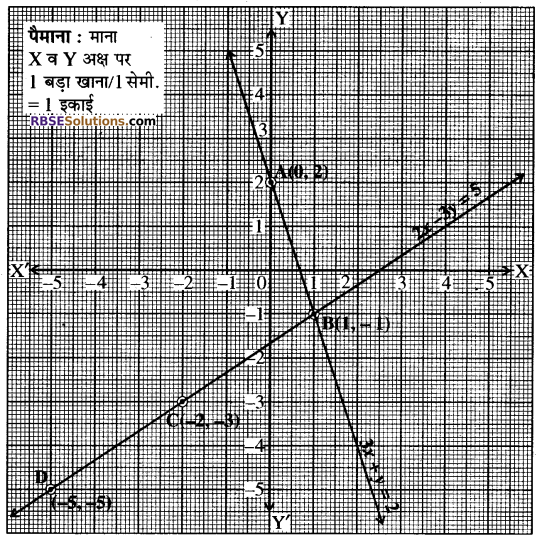

बिन्दुओं A(0, 2) तथा B(1, – 1) को ग्राफ पेपर पर (RBSESolutions.com) आलेखित किया गया और इन्हें मिलाकर 3x + 1 = 2 का ग्राफ प्राप्त किया गया। अब बिन्दु C(-2, – 3) और D- 5, – 5) को ग्राफ पेपर पर आलेखित किया गया और इन्हें मिलाकर 27 – 3y = 5 का ग्राफ आलेखित किया गया। ये दोनों रेखायें बिन्दु (1,-1) पर प्रतिच्छेद करती हैं। अतः x = 1 तथा y = – 1 ही इनका हल है। इस प्रकार दोनों रेखाओं के हल की प्रकृति अद्वितीय हल होगी।
प्रश्न 3.
निम्न रैखिक समीकरणों के युग्मों को आलेखीय विधि से हल कीजिए तथा उन बिन्दुओं के निर्देशांक भी ज्ञात कीजिए जहाँ इनके द्वारा निरूपित रेखाएँ y-अक्ष को काटती हैं।
(i) 2x – 5y + 4 = 0; 2x + y – 8 = 0
(ii) 3x + 2 = 12; 5x – 2y = 4
हल:
(i) दिया गया रैखिक समीकरण युग्म है-
2x – 5y + 4 = 0
2x + y – 8 = 0
2x – 5y + 4 = 0 के ग्राफ के लिए हमें (RBSESolutions.com) प्राप्त है-
5y = 2x +4
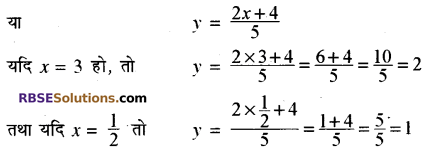
| x | 3 | 0.5 |
| y | 2 | 1 |
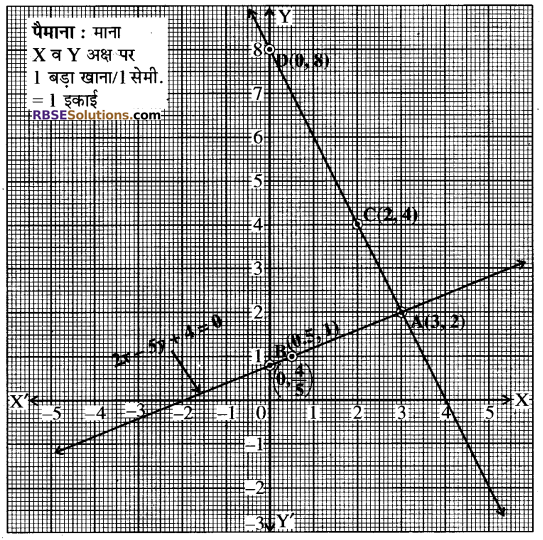
अब, ग्राफ 2x + y – 8 = 0 के लिए (RBSESolutions.com) हमें प्राप्तः है-
2x + y = 8 या y = 8 – 2x
अब यदि x = 2, तब y = 8 – 2 × 2 =8 – 4 = 4
अब यदि x = 3, तब y=8 – 2 × 3 = 8 – 6 = 2
अब यह तालिका हमें प्राप्त हुई-
| x | 2 | 3 |
| y | 4 | 2 |
बिन्दुओं A(3, 2) तथा B(0.5, 1) को ग्राफ पेपर पर आलेखित किया गया तथा इन्हें मिलाकर 2x – 5y + 4 = 0 का ग्राफ प्राप्त किया गया। अब C(2, 4) तथा A(3, 2) को इसी ग्राफ पर आलेखित कर और इनको मिलाकर 2x + y – 8 = 0 का ग्राफ प्राप्त किया गया। ये दोनों रेखायें बिन्दु (3, 2) पर प्रतिच्छेद करती हैं। अतः x = 3 तथा y = 2 ही इनका हल है और दोनों सरल रेखायें -अक्ष को निर्देशांक (0, 0.8) और (0, 8) पर काटती हैं। (RBSESolutions.com) उत्तर
![]()
(ii) दिया गया रैखिक समीकरण युग्म है-


बिन्दु A(4, 0) तथा B(2, 3) को ग्राफ पेपर पर आलेखित किया गया (RBSESolutions.com) तथा इन्हें मिलाकर 3x + 2 = 4 का ग्राफ प्राप्त किया गया। अब B(2, 3) तथा C(0, – 2) को इसी ग्राफ पर आलेखित कर और इनको मिलाकर 5x – 2y = 4 का ग्राफ प्राप्त किया। यह दोनों रेखायें बिन्दु (2, 3) पर प्रतिच्छेद करती हैं। अतः x = 2 तथा y = 3 ही इनका हल है तथा दोनों सरल रेखायें y-अक्ष को निर्देशांक . (0, 6) और (0, -2) पर काटती हैं। उत्तर
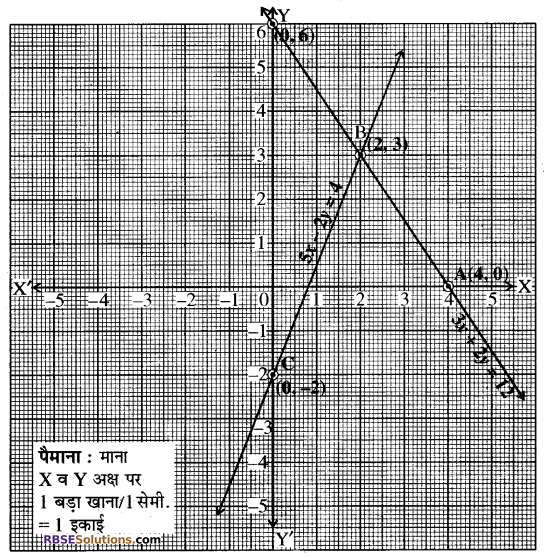
प्रश्न 4.
निम्न रैखिक समीकरण युग्म को आलेखीय विधि द्वारा हल (RBSESolutions.com) कीजिए तथा y-अक्ष तथा युग्म द्वारा निरूपित रेखाओं से निर्मित त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए
4x – 5y = 20, 3x + 5y = 15
हल:


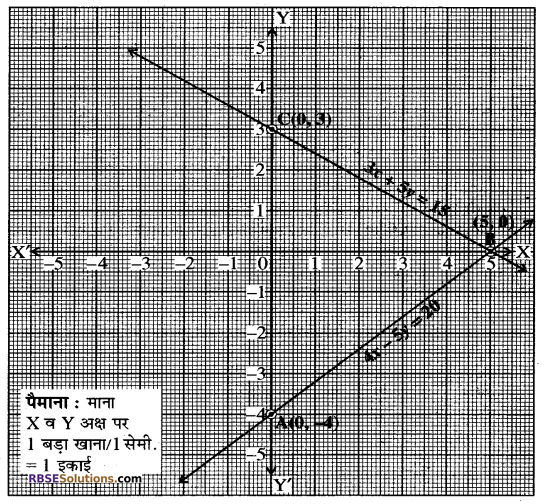
बिन्दुओं A(0, -4) तथा B(5, 0) को ग्राफ पेपर पर आलेखित किया (RBSESolutions.com) गया और इन्हें मिलाकर 4-5y = 20 का ग्राफ प्राप्त किया गया। अब बिन्दु C(0, 3) तथा बिन्दु B(5, 0) को ग्राफ पेपर पर आलेखित किया गया और इन्हें मिलाकर 3x + 5y = 15 का ग्राफ आलेखित किया गया। ये दोनों रेखायें बिन्दु (5, 0) पर प्रतिच्छेद करती हैं। अतः x = 5 तथा y = 0 (शून्य) ही इनका हल है।
y-अक्ष तथा युग्म द्वारा निरूपित रेखाओं से निर्मित त्रिभुज ABC के शीर्षों के निर्देशांक क्रमशः (0, -4), (5, 0) तथा (0, 3) हैं। उत्तर
![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Ex 4.1 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 4 दो चरों वाले रैखिक समीकरण एवं असमिकाएँ Exercise 4.1, drop a comment below and we will get back to you at the earliest.