RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Exercise 5.2.
Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.2
Ex 5.2 Class 10 RBSE Question 1.
Find
(i) 10th term of A.P. 2, 7, 12, ….
(ii) 18th term of A.P. √2, 3√2, 5√2, …..
(iii) 24th term of A.P. 9, 13, 17, 21, ….
Solution :
(i) Given A.P. 2, 7, 12, …..
First term a = 2
Common (RBSESolutions.com) difference d = 7 – 2 = 5
nth term an = a + (n – 1)d
∴ a10 = 2 + (10 – 1) × 5
= 2 + 9 × 5
= 2 + 45
= 47
Hence, 10th term of given series 47.
(ii) Given A.P. √2, 3√2, 5√2, …..
First term a = √2
Common term d = 3√2 – √2
= √2(3 – 1) = 2√2
nth term an = a + (n – 1)d
∴ a18 = √2 + (18 – 1)2√2
= √2 + 17 × 2√2
= √2 + 34√2
= 35√2
Hence a18 = 35√2
(iii) Given A.P. 9, 13, 17, 21, …..
First term a = 9
common (RBSESolutions.com) difference
d = 13 – 9 = 4
nth term an = a + (n – 1)d
∴ a24 = 9 + (24 – 1) × 4
= 9 + 23 × 4
= 9 + 92
= 101
Hence a24 = 101
RBSE Solutions For Class 10 Maths Chapter 5.2 Question 2.
Solve
(i) Which term of A.P. 21, 18, 15, …… is – 81?
(ii) Which term of AP. 84, 80, 76, …. is zero ?
(iii) Is 301 any term of series 5, 11, 17, 23, …… ?
(iv) Is -150 is any term of A.P. 11, 8, 5, 2, …….
Solution :
(i) Given A.P. 21, 18, 15, ….
First term (a) = 21
Common (RBSESolutions.com) difference
(d) = 18 – 21 = -3
∵ an = a + (n – 1)d
According to question
-81 = 21 + (n – 1)(-3)
⇒ -81-21 = (n – 1) × -3
⇒ -102 = (n – 1) × -3
⇒ (n – 1) = \(\frac { -102 }{ -3 }\)
⇒ n – 1 = 34
⇒ n = 34 + 1 = 35
Hence, 35th term of given series is -81.
(ii) Given A.P. 84, 80, 76…..
First term (a) = 84
Common (RBSESolutions.com) difference (d) = 80 – 84 = -4
∵ an = a + (n – 1)d
According to question,
0 = 84 + (n – 1)(-4)
⇒ -84 = (n – 1) × -4
⇒ (n – 1) = \(\frac { -84 }{ -4 }\)
⇒ n – 1 = 21
⇒ n = 21 + 1 = 22
Hence. 22nd term of given A.P. is zero.
(iii) Given A.P. 5, 11, 17, 23 …..
First term (a) = 5
Common difference
(d) = 11 – 5 = 6
∵ an = a + (n – 1)d
According to (RBSESolutions.com) question.,
⇒ 301 = 5 + (n – 1)(6)
⇒ 301 – 5 = 6(n—1)
⇒ 6(n – 1) = 296
⇒ (n – 1) = \(\frac { 296 }{ 6 }\)
⇒ n – 1 = 49.33
⇒ n = 49.33 + 1 = 50.33
∴ Value of n cannot be fraction, it means n is not a whole number. Thus no term can be 301 in given series A.P.
(iv) Given A.P. : 11, 8, 5, 2 …
First term (a) = 11 and common difference (d) = 8 – 11 = – 3
Let nth term, an = -150
⇒ a + (n – 1)d = -150
⇒ 11 + (n – 1) × (-3) = -150
⇒ -3(n – 1) = -150 – 11 = -161
⇒ (n – 1) = \(\frac { -161 }{ -3 }\)
= 53.6 (approx)
∴ n = 53.6 + 1 = 54.6
⇒ n is not a whole no.
Hence, -150 is no (RBSESolutions.com) term is given A.P.
Exercise 5.2 Class 10 RBSE Question 3.
If 6th term and 17th turn of A.P. are 19 and 41 respectively, then find 40th term.
Solution :
Given
6th term a6 = 19
and 17th term a17 = 41
40th term a40 = ?
nth term, a = a + (n – 1)d
a6 = a + (6 – 1)d
⇒ 19 = a + 5d …..(i)
and a17 = a + (17 – 1)d
⇒ 41 = a + 16 d …(ii)
On subtracting (i) from (ii)
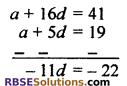
d = 2
Putting d = 2 in (RBSESolutions.com) equation (i)
a + 5 × 2 = 19
a = 19 – 10
a = 9
Thus, a40 = a + (40 – 1)d
= 9 + 39 × 2
= 9 + 78 = 87
Hence, 40th term of A.P. is 87.
RBSE Solutions For Class 10 Maths Chapter 5 Question 4.
Third and ninth term of an A.P. (RBSESolutions.com) are 4 and -8 respectively, then its which term will be zero?
Solution :
Let a is first term of A.P. and d is common difference.
Given, third term a3 = 4
a + (3 – 1)d = 4, [an = a + (n – 1)d]
⇒ a + 2d = 4
and ninth term a9 = -8
a + (9 – 1)d = -8
⇒ a + 8d = -8 …(ii)
Subtracting equation (i) from (ii)
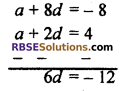
d = \(\frac { -22 }{ -11 }\)
∴ d = \(\frac { -12 }{ 6 }\) = -2
Putting this value (RBSESolutions.com) of d in equation (i)
a + 2(-2) = 4
or a – 4 = 4
∴ a = 4 + 4 = 8
Let nth term of series will be zero, than nth term
nth term an = 0
∴ a + (n – 1)d = 0
⇒ 8 + (n – 1) × (-2) = 0
⇒ -2(n – 1) = -8
⇒ (n – 1) = 4
∴ n = 5
Hence, 5th term of AP. will be zero
RBSE Class 10 Maths Chapter 5 Question 5.
Third term of an A.P. Is 16 and 7th term is 12 more than (RBSESolutions.com) 5th term, then find AP.
Solution :
Let first term of A.P. is a and common difference is d.
Given a3 = 16
a + (3 – 1)d = 16
⇒ a + 2d = 16 …(i)
According to question, a7 = 12 – a5
⇒ a7 – a5 = 12
[a + (7 – 1)d] – [a+(5 – 1)d] = 12
⇒ a7 + 6d – a – 4d = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
d = \(\frac { 12 }{ 2 }\) = 6
Substituting value of d in equation (i)
a + 2(6) = 16
∴ a = 16 – 12 = 4
AP. a, a + d, a + 2d,…
= 4, 4 + 6, 4 + 2 × 6,…
= 4, 10, 16,…
Hence, required A.P. is 4, 10, 16, 22,…
RBSE Class 10 Maths Chapter 5.2 Question 6.
How many three digit (RBSESolutions.com) numbers are divisible by 7 ?
Solution :
Series of 3 digit numbers 100, 101, 102, …….. 999,
First three digit number divisible by 7 = 105 and last number = 994
Then series of three digit numbers divisible by 7
105, (105 + 7), (105 + 7+ 7), …. 994 = 105, 112, 119, …,994
Let total number of terms is n.
First term a = 105, common difference d = 7,
∴ nth term an = 994
⇒ a + (n – 1)d = 994
⇒ 105 + (n – 1) × 7 = 994
⇒ (n – 1) × 7=994 – 105 = 889
⇒ (n – 1) = \(\frac { 889 }{ 7 }\) = 127
∴ n = 127 +1 = 128
Hence, three digit number divisible by 7 is 128.
Class 10 Maths RBSE Solution Chapter 5 Question 7.
Find 11th term from (RBSESolutions.com) last of A.P. 10, 7, 4, …., -62
Solution :
Given A.P. 10, 7, 4….., -62
First term (a) = 10
Common difference (d) = 7 – 10 = – 3
Last term an = -62
Formula, rth term from last
= an – (r – 1)d
11th term from last = -62 – (11 – 1) × (-3)
= -62 – 10(-3)
= -62 + 30
= -32
Hence, 11th term from last of A.P. = 32.
RBSE Class 10 Maths Chapter 5 Exercise 5.2 Question 8.
Find the 12th term from (RBSESolutions.com) last of A.P. 1, 4, 7, 10, …., 88
Solution :
Given A.P. 1, 4, 7, 10……, 88
First term (a) = 1
Common difference (d) = 4 – 1 = 3
Last term an = 88
Formula, rth term from last
= an – (r – 1)d
12th term from last = 88 – (12 – 1) × 3
= 88 – 11 × 3
= 88 – 33 = 55
Hence, 12th term from last term of A.P will be 55.
Chapter 5 Class 10 Maths RBSE Question 9.
There are 60 terms in an AP. If its first and (RBSESolutions.com) last term are 7 and 125 respectively, then find its 32nd term.
Solution :
Number of terms (n) = 60
First term (a) = 7
Last term (an) = 125
Formula, an = a + (n – 1)d
⇒ 125 = 7 + (60 – 1)d
⇒ 125 – 7 = 59 d
⇒ 118 = 59 d
⇒ d = \(\frac { 118 }{ 59 }\)
⇒ d = 2
Thus, 32nd term
a32 = a + (32 – 1)d
= 7 + 31 × 2
= 7 + 62 = 69
Hence, 32nd term of A.P. is 69.
RBSE Class 10 Chapter 5 Question 10.
Four numbers are ¡n A.P. If sum of (RBSESolutions.com) numbers is 50 and larger number is 4 times the smaller number, then find the number.
Solution :
Let four numbers in A.P. are
a, a + d, a + 2d, a + 3d
According to question
a + (a + d) + (a + 2d) + (a + 3d) = 50
⇒ 4a + 6d = 50
⇒ 2(2a + 3d) = 50
⇒ 2a + 3d = 25 …..(i)
If larger number is 4 times the smaller (RBSESolutions.com) number, then equation will be as follow,
a + 3d = 4 x a
⇒ a + 3d = 4a
⇒ 3d = 3a
⇒ d = a …(ii)
from equation (i) and (ii)
2a + 3a = 25 [∴ d = a]
a = 25
a = 5
∴ d = 5 [∵ eqn(ii)]
∴ Numbers a = 5
a + d = 5 + 5 = 10
a + 2d = 5 + 2 × 5 = 15
a + 3d = 5 + 3 × 5 = 20
Hence, four numbers are 5, 10, 15, and 20
We hope the given RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Exercise 5.2, drop a comment below and we will get back to you at the earliest.