RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Exercise 5.3.
Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3
Ex 5.3 Class 10 RBSE Question 1.
Find the sum of the (RBSESolutions.com) following A.P.’s
(i) 1, 3, 5, 7, …, upto 12 terms
(ii) 8, 3, -2, …, upto 22 terms
(iii) \(\frac { 1 }{ 15 } ,\frac { 1 }{ 22 } ,\frac { 1 }{ 10 } ,….\) upto 11 terms
Solution :
(i) Given A.P. 1, 3, 5, 7 ….. upto 12 terms
First term (a) = 1
Common difference (d) = 3 – 1 ⇒ 2
Sum of n terms
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
S12 = \(\frac { 12 }{ 2 }\) [2 × 1 + (12 – 1)2]
= 6[2 + 11 × 2]
= 6[2 + 22]
= 6 × 24
= 144
Hence, sum of first 12 terms = 144.
(ii) Given. A.P. 8, 3, -2, …, upto 22 terms
First term (a) = 8
common (RBSESolutions.com) difference (d) = 3 – 8 = -5
sum of n terms
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
= \(\frac { 22 }{ 2 }\) [2 × 8 + (22 – 1)(-5)]
= 11[16 + 21 × -5]
= 11[16 – 105]
= 11 [- 89]
= -979
Hence, sum of first 22 terms is -979.
(iii) GivenA.P. \(\frac { 1 }{ 15 } ,\frac { 1 }{ 12 } ,\frac { 1 }{ 10 } ,….\) upto 11 terms
First term (a) = \(\frac { 1 }{ 15 }\)
Common difference (d) = \(\frac { 1 }{ 12 }\) – \(\frac { 1 }{ 15 }\)
= \(\frac { 15-12 }{ 180 }\) = \(\frac { 3 }{ 180 }\) = \(\frac { 1 }{ 60 }\)
and number (RBSESolutions.com) of term n = 11
∵ Sum of n terms Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]

Hence, sum of first 11 terms of series = \(\frac { 33 }{ 20 }\)
Arithmetic Progression Class 10 RBSE Question 2.
Find the sum of the (RBSESolutions.com) following :
(i) 3 + 11 + 19 + … 803
(ii) 7 + 10\(\frac { 1 }{ 2 }\) + 14 + …… + 84
Solution :
(i) Given :
3 + 11 + 19 + … + 803
Here first term a = 3
Common difference d = 11 – 3 = 8
If 803 is nth term of given A.P, then
nth term, an = 803
a + (n – 1)d = 803
3 + (n – 1)8 = 803
(n – 1)8 = 803 – 3
n – 1 = \(\frac { 800 }{ 8 }\)
n – 1 = 100
n = 100 + 1
n = 101
Hence, A.P. has 101 terms.
∴ Sum of n terms
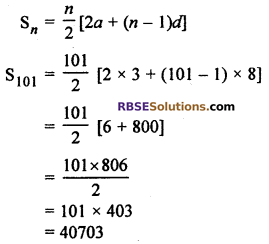
Thus, 3 + 11+ 15 + … + 803 = 40703.
(ii) Given
7 + 10\(\frac { 1 }{ 2 }\) + 14 + …. + 84
Here, First term (a) = 7
common difference (d) = 10\(\frac { 1 }{ 2 }\) – 7 = 3\(\frac { 1 }{ 2 }\)
= \(\frac { 7 }{ 2 }\)
If 84 is nth term of given (RBSESolutions.com) series, then
∴ nth term an = 84
a + (n – 1)d = 84
⇒ 7 + (n – 1) \(\frac { 7 }{ 2 }\) = 84
⇒ 1 + \(\frac { n-1 }{ 2 }\) = 12
⇒ \(\frac { n-1 }{ 2 }\) = 12 – 1
⇒ \(\frac { n-1 }{ 2 }\) = 11 ⇒ n – 1 = 22
n = 22 + 1 = 23
There are 23 terms in series
Sum of 23 terms
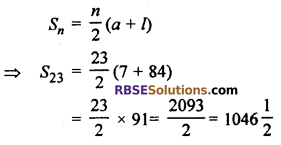
Hence, 7 + 10\(\frac { 1 }{ 2 }\) + 14 + …… + 84 = 1046\(\frac { 1 }{ 2 }\)
RBSE Solutions For Class 10 Maths Chapter 5 Question 3.
Find the number of terms
(i) How many (RBSESolutions.com) terms of the A.P. : 9, 17, 25 ….. must be taken to give a sum of 636?
(ii) How many terms the A.P. 63, 60, 57, …… must be taken to give a sum of 693?
Solution :
(i) Given A.P. : 9, 17, 25, …
First term (a) = 9, common difference (d) = 17 – 9 = 8
Let no. of terms be n
Sn = 636
⇒ \(\frac { n }{ 2 }\) [2a + (n – 1)d] = 636
⇒ \(\frac { n }{ 2 }\) [2 × 9+ (n – 1)8] = 636
⇒ \(\frac { n }{ 2 }\) [18 + 8n – 8] = 636
⇒ \(\frac { n }{ 2 }\) [8n + 10] = 636
⇒ n(4n + 5) = 636
⇒ 4n2 + 5n = 636
⇒ 4n2 + 5n – 636 = 0
⇒ 4n2 + 53 n – 48n – 636 = 0
⇒ n(4n + 53) – 12(4n + 53) = 0
⇒ (4n + 53)(n – 12) = 0
⇒ n – 12 = 0 or 4n + 53 = 0
⇒ n = 12 or – \(\frac { 53 }{ 4 }\)
∵ n cannot be (RBSESolutions.com) negative
So, ignore n = – \(\frac { 53 }{ 4 }\)
∴ n = 12
Hence, sum of 12 terms of given A.P. is 636.
(ii) Given A.P. 63, 60, 57 …..
First term(a) = 63
Common difference (d) = 60 – 63 = -3
Let number of terms be n
Sn = 693
We know that
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
⇒ 693 = \(\frac { n }{ 2 }\) [2 × 63 + (n – 1) (-3)]
⇒ 693 = \(\frac { n }{ 2 }\) [126 – 3n + 3]
⇒ 1386 = n(129 – 3n)
⇒ 1386 = 129n – 3n2
⇒ 3n2 – 129n + 1386 = 0
⇒ n2 – 43n + 462 = 0
⇒ n2 – 21n – 22n + 462 = 0
⇒ = n(n – 21) – 22(n – 21) = 0
⇒ (n – 21)(n – 22) = 0
⇒ n – 21 = 0 or n – 22 = 0
n = 21 or n = 22
By taking 21 or 22 terms (RBSESolutions.com) of given A.P. we will get sum 693.
RBSE Class 10 Maths Chapter 5 Question 4.
Find the sum of first 25 terms of following series whose th term is given :
(i) an = 3 + 4n
(ii) an = 7 – 3n
Solution :
(i) Given an = 3 + 4n …..(i)
Substituting various values of n in equation (i)
a1 = 3 + 4(1) = 7
a2 = 3 + 4(2) = 11
a3 = 3 + 4(3) = 15, …
common difference (d) = a2 – a1 = 11 – 7 = 4
a3 – a2 = 15 – 11 = 4
∵ a2 – a1 = a3 – a2 = 4
Thus series is 7, 11, 15 ….
and given series (RBSESolutions.com) is an A.P.
Here, a = 7, d= 4 and n = 25
∵ Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
S25 = \(\frac { 25 }{ 2 }\) [2 × 7 + (25 – 1)4]
= \(\frac { 25 }{ 2 }\) [14 + 24 × 4]
= \(\frac { 25 }{ 2 }\) [14 + 96]
= \(\frac { 25 }{ 2 }\) × 110
= 25 × 55
= 1375
Thus S25 = 1375
(ii)Given : an = 7 – 3n
substituting various values (RBSESolutions.com) of n in equation (i)
a1 = 7 – 3(1) = 4
a2 = 7 – 3(2) = 1
a3 = 7 – 3(3) = -2
common difference (d) = a2 – a1 = 1 – 4 = -3
and a3 – a2 = -2 – 1 = -3
∵ a2 – a1 = a3 – a2 = -2 – 1 = -3
Thus A.P. is 4, 1, -2,…
Here a = 4 d = -3 and n = 25
We have to find sum of first 25 terms
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
Sn = \(\frac { 25 }{ 2 }\) [2 x 4 + (25 – 1)(-3)
= \(\frac { 25 }{ 2 }\) [8 + 24 × -3]
= \(\frac { 25 }{ 2 }\) [8 – 72]
= \(\frac { 25 }{ 2 }\) × – 64
= -25 × 32
= -800
Hence S25 = – 800.
RBSE Solutions For Class 10 Maths Chapter 5.3 Question 5.
Find the sum of first 51 terms of AP. in (RBSESolutions.com) which IInd and IIIrd term are 14 and 18 respectively.
Solution :
Second term of A.P. a2 = 14
and third term a3 = 18
∴ Common difference d = a3 – a2
= 18 – 14 = 4
Again, ∵ IInd term = 14
∴ a + d = 14
⇒ a + 4 = 14
⇒ a = 14 – 4
⇒ a = 10
∵ a = 10, d = 4
Then, sum of n terms Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
∴ S51 = \(\frac { 51 }{ 2 }\) [2 × 10 + (51 – 1)4]
= \(\frac { 51 }{ 2 }\) [20 + 50 × 4]
= \(\frac { 51 }{ 2 }\) [20 + 200]
= \(\frac { 51 }{ 2 }\) × 220 = 51 × 110 = 5610
Hence, sum of 5 terms of given A.P. = 5610
Exercise 5.3 Class 10 RBSE Question 6.
The first and last term of an A.P. are 17 and 350 respectively. If (RBSESolutions.com) common difference is 9 then find number of terms in A.P. and their sum.
Solution :
Given
First term (a) = 17
Last term (l) = an = 350
and common difference (d) = 9
∵ an = 350
a + (n – 1)d = 350
⇒ 17 + (n – 1)9 = 350
⇒ 9(n – 1) = 350 – 17 = 333
⇒ n – 1 = \(\frac { 333 }{ 9 }\) = 37
∴ n = 37 + 1 = 38
Now, Sn = \(\frac { n }{ 2 }\)(a + l)
∴ = \(\frac { 38 }{ 2 }\) (17 + 350)
= 19 × 367 = 6973
Hence, n = 38 and sum of term (Sn) = 6973
RBSE Solutions For Class 10 Maths Chapter 5 Miscellaneous Question 7.
Find the sum of all odd numbers, (RBSESolutions.com) divisible by 3 between 1 and 1000.
Solution :
Odd numbers divisible by 3, between 1 and 1000 are 3, 9, 15, 21 …….. 999.
Clearly series 3, 9, 15, 15,21 …… 999 is A.P.
whose first term (a) = 3 and common difference (d) = 6.
Let us assume that this series contains n terms.
∴ an = 999
⇒ a + (n – 1)d = 999
⇒ 3 + (n – 1) × 6 = 999
⇒ 6n – 3 = 999
⇒ 6n = 1002
⇒ n = \(\frac { 1002 }{ 6 }\)
⇒ n = 167
∴ Required sum
Sn = \(\frac { n }{ 2 }\) (a + l)
S167 = \(\frac { 167 }{ 2 }\) (3 + 999)
= \(\frac { 167 }{ 2 }\) × 1002
= 167 × 501
= 83667
Hence, required sum = 83667.
RBSE Class 10 Maths Chapter 5.3 Question 8.
The first term of A.P. is 8, nth term is 33 and sum (RBSESolutions.com) of first n terms is 123, then find n and common difference d.
Solution :
Given
First term (a) = 8
nth term (an) = 33
sum of n terms (Sn) = 123
∵ nth term an = a + (n – 1)d
⇒ 33 = 8 + (n – 1)d
⇒ (n – 1)d = 33 – 8
⇒ (n – 1)d = 25 ……(i)
Now, sum of n terms
Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
⇒ 123 = \(\frac { n }{ 2 }\) [2 × 8 + 25] [From equation (i)]
⇒ 123 = \(\frac { n }{ 2 }\) (16 + 25)
⇒ 123 = \(\frac { n }{ 2 }\) × 41
⇒ n = \(\frac { 123\times 2 }{ 41 }\)
⇒ n = 6
Put the value of n in equation (i)
⇒ (6 – 1)d = 25
⇒ 5d = 25
⇒ d = 5
Thus, n = 6 and d = 5
RBSE Solutions For Class 10 Maths Chapter 5.3 Question 9.
A sum of ₹ 280 is to be used to give four (RBSESolutions.com) cash prize. If each prize is ₹ 20 less than its preceding prize. Find the value of each of the prizes.
Solution :
Let first prize is ₹ a
∴ IInd prize a2 = ₹ (a – 20)
IIIrd prize a3 = ₹ [(a – 20) – 20]
a3 = ₹ (a – 40)
IVth prize a4 = ₹ [(a – 40) – 20)]
a4 = ₹ (a – 60)
Here first term = a,
Common difference d = (a – 20) – a
d = -20
Number of terms n = 4
Sum of terms Sn = 280
By Formula, Sn = \(\frac { n }{ 2 }\) [2a + (n – 1)d]
S4 = \(\frac { 4 }{ 2 }\) [2a + (4 – 1) × -20]
⇒ 280 = 2[2a + 3 × – 20]
⇒ 280 = 2[2a – 60]
⇒ 140 = 2a – 60
⇒ 2a = 140 + 60
⇒ a = \(\frac { 200 }{ 2 }\) = 100
Hence Ist prize = 100, remaining (RBSESolutions.com) prize are ₹ (100 – 20), ₹ (100 – 20 – 20) and ₹(100 – 20 – 20 – 20).
Hence price are ₹ 100, ₹ 80, ₹ 60, and 40
Class 10 Maths RBSE Solution Chapter 5 Question 10.
A manufacturer of TV sets produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production increases uniformly by a fixed number every year, find
(i) the production in the Ist year.
(ii) The production in the 10th year.
(iii) The total production in first 7 years.
Solution :
(i) Let production of T.V. sets in first years is a. (RBSESolutions.com) Given that production of T.V. sets in third year
a3 = 600
and in seventh year
a7 = 100.
Now, a3 = a + (3 – 1)d
600 = a + 2d …..(i)
and a7 = a + (7 – 1)d
700 = a + 6d …(ii)
subtracting eqn (i) from (ii),
100 = 4d
d = \(\frac { 100 }{ 4 }\) = 25
Put the value of d in (RBSESolutions.com) equation (i)
⇒ 600 = a + 2 × 25
⇒ 600 = a + 50
⇒ a = 600 – 50
⇒ a = 550
Production of T.V. set in Ist year = 550
(ii) Production of TV. sets in 10th year
Formula, an = a + (n – 1)d
an = 550 + (10 – 1)25
= 550 + 9 × 25
= 550 + 225 = 775
Thus, production (RBSESolutions.com) of T.V. sets in 10th year = 775 sets
(iii) Total production in 7 years
Sn = \(\frac { 7 }{ 2 }\) [2a + (n – 1)d]
By formula, S7 = \(\frac { 7 }{ 2 }\) [2 × 550 + (7 – 1)25]
= \(\frac { 7 }{ 2 }\) [1100 + 6 × 25]
= \(\frac { 7 }{ 2 }\) [1100 + 150]
= \(\frac { 7 }{ 2 }\) × 1250 = 7 × 625
= 4375
Thus, total production in 7 years in 4375 etc.
We hope the given RBSE Solutions for Class 10 Maths Chapter 5 Arithmetic Progression Ex 5.3 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 5 Arithmetic Progression Exercise 5.3, drop a comment below and we will get back to you at the earliest.