RBSE Solutions for Class 10 Maths Chapter 5 समान्तर श्रेढ़ी Ex 5.3 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 5 समान्तर श्रेढ़ी Exercise 5.3.
| Board | RBSE |
| Textbook | SIERT, Rajasthan |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 5 |
| Chapter Name | समान्तर श्रेढ़ी |
| Exercise | Exercise 5.3 |
| Number of Questions Solved | 10 |
| Category | RBSE Solutions |
Rajasthan Board RBSE Class 10 Maths Chapter 5 समान्तर श्रेढ़ी Ex 5.3
प्रश्न 1.
निम्नलिखित समान्तर श्रेढ़ियों का (RBSESolutions.com) योगफल ज्ञात कीजिए
(i) 1, 3, 5, 7, …., 12 पदों तक
(ii) 8, 3, – 2, …., 22 पदों तक
(iii) \(\frac{1}{15}, \frac{1}{12}, \frac{1}{10}, \ldots \ldots, 11\) पदों तक
हल:
(i) दिया है- a = 1, d = 5 – 3 = 2 और n = 12 है। हम जानते हैं-
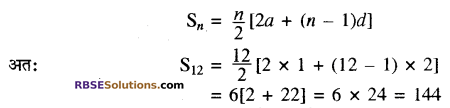
इसलिए दी हुई A.P के प्रथम 12 पदों का योग 144 है। उत्तर
(ii) दिया है-a = 8, d = 3 – 8 = – 5 और n = 22 है। (RBSESolutions.com) हम जानते हैं कि
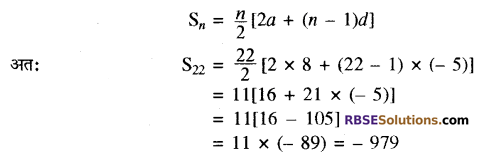
इसलिए दी हुई A.P के प्रथम 22 पदों का योग – 979 है। उत्तर
(iii) दिया है- \(a=\frac{1}{15}, d=\frac{1}{12}-\frac{1}{15}=\frac{1}{60}\) और n = 11 हम जानते हैं कि

इसलिए दी हुई A.P के प्रथम 11 पदों का (RBSESolutions.com) योग \(\frac{33}{20}\) है। उत्तर
![]()
प्रश्न 2.
निम्नलिखित का योगफल ज्ञात कीजिए-
(i) 3 + 11 + 19 +, …., + 803
(ii) 7 + \(10 \frac{1}{2}\) + 14 + ,…, + 84
हल:
(i) यहाँ अन्तिम पद दिया है। पहले हमें पदों की संख्या ज्ञात करनी होगी। दिया है-a = 3, d = 11 – 3 = 8, l = an = 803
इसलिए an = a + (n – 1)d
मान रखने पर
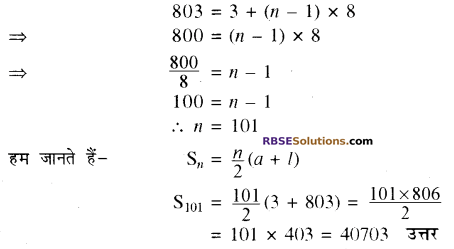
(ii) यहाँ अन्तिम पद दिया है। पहले हमें पदों की (RBSESolutions.com) संख्या ज्ञात करनी होगी। \(a=7, d=10 \frac{1}{2}-7=3 \frac{1}{2}=\frac{7}{2}\), an = l = 84
हम जानते हैं-
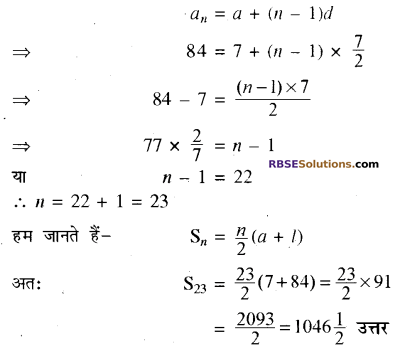
प्रश्न 3.
पदों की संख्या ज्ञात कीजिए
(i) समान्तर श्रेढ़ी 9, 17, 25, ….. के कितने पद लिए जायें कि उनका (RBSESolutions.com) योगफल 636 हो ?
(ii) समान्तर श्रेढ़ी 63, 60, 57, ….. के कितने पद लिए जायें कि उनका योगफल 693 हो ?
हल:
(i) दिया है-A.P 9, 17, 25, …
यहाँ a = 9, d = 17 – 9 = 8
क्योंकि Sn = 636

अतः दी गई A.P के 12 पदों का (RBSESolutions.com) योग 636 है। उत्तर
(ii) दिया है-A.P 63, 60, 57, …..
यहाँ a = 63, d = 60 – 63 = – 3, Sn = 693
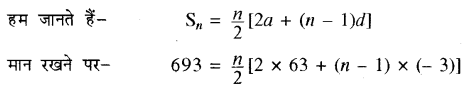
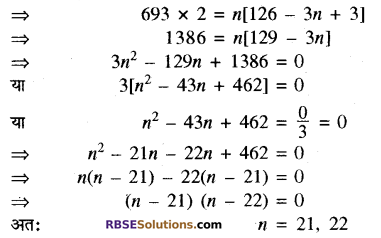
अतः दी गई A.P के 21 या 22 पदों का योग 693 है। उत्तर
![]()
प्रश्न 4.
निम्न श्रेढ़ियों के पहले 25 पदों का योगफल ज्ञात (RBSESolutions.com) कीजिए जिसका वाँ पद दिया है
(i) an = 3 + 4n
(ii) an = 7 – 3n
हल:
(i) दिया है-an = 3 + 4n n = 1, 2, 3, 4, ….. n रखने पर
श्रेढ़ी 7, 11, 15, 19, ….. (3 + 4n) एक समान्तर श्रेढ़ी है, जिसका सार्वअन्तर d = 4 है।
हम जानते हैं-
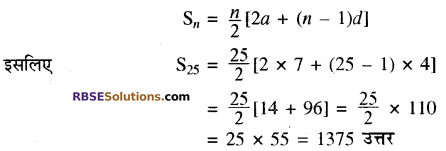
(ii) दिया है-an = 7 – 3 n
n = 1, 2, 3, 4, ….. n रखने पर
श्रेढी 4, 1, – 2, 5, – 8…… (7 – 3n) एक समान्तर श्रेढ़ी है, (RBSESolutions.com) जिसका प्रथम पद a = 4 और सार्वअन्तर d = 1 – 4 = – 3 है।

प्रश्न 5.
एक समान्तर श्रेढ़ी के पहले 51 पदों का योग ज्ञात कीजिये जिसमें द्वितीय तथा तृतीय पद क्रमशः 14 तथा 18 हैं।
हल:
माना कि ‘a’ और ‘d’ प्रथम पद और सार्व (RBSESolutions.com) अन्तर है।
दिया गया है कि a2 = 14; a3 = 18
और n = 51

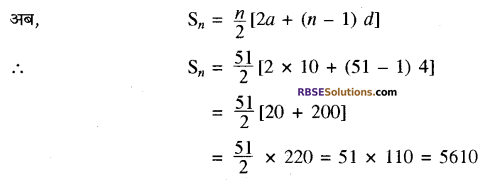
अतः, दी गई A.P के प्रथम 51 पदों का योग 5610 है। उत्तर
प्रश्न 6.
किसी समान्तर श्रेढ़ी का प्रथम एवं (RBSESolutions.com) अन्तिम पद क्रमशः 17 और 350 हैं। यदि सार्वअन्तर 9 हो तो समान्तर श्रेढ़ी में पदों की संख्या कितनी है तथा उनका योग क्या है?
हल:
दिया है कि प्रथम पद = a= 17;
अन्तिम पद = l = an = 350
और सार्व अन्तर= d= 9
∵ l = an = 350
a + (n – 1) d= 350
17 + (n – 1)9 = 350
या 9 (n – 1) = 350 – 17 = 333
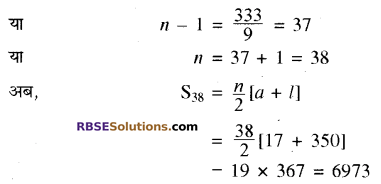
अतः दी गई A.P के 38 पदों का योग 6973 है। उत्तर
![]()
प्रश्न 7.
1 से 1000 के बीच 3 से भाज्य सभी (RBSESolutions.com) विषम संख्याओं का योगफल ज्ञात कीजिए।
हल:
1 से 1000 के बीच 3 से भाज्य विषम संख्याएँ निम्न होंगी-
3, 9, 15, 21, ….., 999 एक समान्तर श्रेणी है।
अतः यहाँ पर दिया गया है-
प्रथम पद (a) = 3,
सार्वअन्तर (d) = 9 – 3 = 6,
l = an = 999
हम जानते हैं-
an = a + (n – 1)d
मान रखने पर-
999 = 3 + (n – 1) × 6
⇒ 996 = (n – 1) × 6
⇒ \((n-1)=\frac{996}{6}=166\)
n = 166 + 1 = 167
हमें यहाँ पर 1 से 1000 के बीच 3 से भाज्य (RBSESolutions.com) विषम संख्याओं का योग ज्ञात करना है। इसलिए
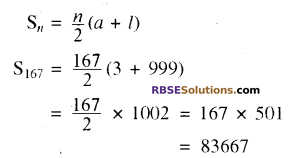
अतः अभीष्ट योगफल = 83667 उत्तर
प्रश्न 8.
एक समान्तर श्रेढ़ी में प्रथम पद 8 है, nवाँ घद 33 है तथा पहले n पदों का (RBSESolutions.com) योग 123 है तो n तथा सार्वअन्तर d को ज्ञात कीजिए।
हल:
दिया है-

अतः n = 6 तथा d = 5 है। उत्तर
![]()
प्रश्न 9.
280 रु. की राशि चार पुरस्कार देने के लिए रखी गई है। (RBSESolutions.com) यदि प्रथम पुरस्कार के बाद का प्रत्येक पुरस्कार, अपने ठीक पहले पुरस्कार से 20 रु. कम हो, तो प्रत्येक पुरस्कार की राशि ज्ञात कीजिए।
हल:
माना कि पुरस्कार क्रमवार a – 3d, a – d, a + d तथा a + 3d है।
इसलिए इनका योग करने पर
a – 3d + a – d + a + d + a + 3d = 280
⇒ 4a = 280
या \(a=\frac{280}{4}=70\)
प्रश्नानुसार दिया गया है-
(a – 1) – (a – 3d) = 20
⇒ a – d – a + 3d = 20
⇒ 2d = 20
∴ \(d=\frac{20}{2}=10\)
इसलिए चार पुरस्कार रुपयों में (RBSESolutions.com) इस प्रकार हैं-
70 – 3 × 10, 70 – 10, 70 + 10, 70 + 3 × 10
40, 60, 80, 100
अतः पहला पुरस्कार ₹ 100, शेष पुरस्कार क्रम से ₹ 20 – 20 कम है।
अतः पुरस्कार ₹ 100, ₹ 80, ₹ 60 और 40 है। उत्तर
प्रश्न 10.
एक टेलीविजन सेटों का निर्माता, तीसरे वर्ष 600 टी.वी. तथा सातवें वर्ष में 700 टी.वी. सेटों का उत्पादन करता है। यह मानते हुए कि प्रत्येक वर्ष उत्पादन में एक समान रूप से एक निश्चित संख्या में वृद्धि होती है, ज्ञात कीजिए
(i) प्रथम वर्ष में उत्पादन
(ii) 10वें वर्ष में उत्पादन
(iii) 7 वर्षों में कुल उत्पादन
हल:
(i) चूंकि प्रत्येक वर्ष उत्पादन में समान रूप से (RBSESolutions.com) एक निश्चित संख्या में वृद्धि होती है, इसलिए पहले, दूसरे, तीसरे…. वर्षों में उत्पादित टी.वी. सेटों की संख्याएँ एक A.P में होंगी। आइये हम यदि वें वर्ष में उत्पादित टी.वी. सेटों की, संख्या को an से व्यक्त करें।
दिया गया है|-
a3 = 600 तथा a7 = 700
प्रश्नानुसार a3 = a + 2d = 600 …..(1)
और a7 = a + 6d = 700 …..(2)
समीकरण (2) में से (1) को घटाने पर
4d = 100
∴ \(d=\frac{100}{4}=25\)
d का मान समीकरण (1) में रखने पर हमें a = 550 प्राप्त होता है। अतः प्रथम वर्ष में उत्पादित टी.वी. सेटों की संख्या 550 है। उत्तर
(ii) अब
a10 = a + (10 – 1)d = a + 9d
मान रखने पर a10 = 550 + 9 × 25
a10 = 550 + 225
= 775
अतः 10वें वर्ष में उत्पादित टी.वी. सेटों की (RBSESolutions.com) संख्या 775 है। उत्तर
(iii) साथ ही
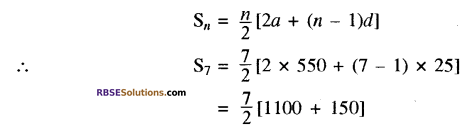
\(\begin{aligned}=\frac{7 \times 1250}{2} &=7 \times 625 \\ &=4375 \end{aligned}\)
अतः प्रथम 7 वर्षों में कुल उत्पादित हुए सभी टी.वी. सेटों की संख्या 4375 है। उत्तर
![]()
We hope the RBSE Solutions for Class 10 Maths Chapter 5 समान्तर श्रेढ़ी Ex 5.3 help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 5 समान्तर श्रेढ़ी Exercise 5.3, drop a comment below and we will get back to you at the earliest.