RBSE Solutions for Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions

RBSE Solutions for Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions.

Rajasthan Board RBSE Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions

Multiple Choice Questions
Question 1.
It tan θ = 1, then (RBSESolutions.com) cos θ will be :
(A) 1
(B) \(\frac { 1 }{ 2 }\)
(C) \(\frac { \sqrt { 3 } }{ 2 }\)
(D) \(\frac { 1 }{ \sqrt { 2 } }\)
Solution :
tan θ = 1
⇒ tan θ = tan 45°
∴ θ = 45°
cos 45° = \(\frac { 1 }{ \sqrt { 2 } }\)
Hence, option (D) is correct.

Question 2.
If sin θ = cos θ (θ = acute angle), then value of θ will be ;
(A) 30°
(B) 45°
(C) 60°
(D) 75°
Solution :
sin θ = cos θ
⇒ \(\frac { sin\theta }{ cos\theta } \) = 1
⇒ tan θ = 1
⇒ tan θ = tan 45°
∴ θ = 45°
Hence, option (B) is correct.

Question 3.
value of 2 sin² 60° + 3 cot² 30° – tan 45° is.
(A) \(\frac { 2 }{ 19 }\)
(B) \(\frac { 12 }{ 19 }\)
(C) \(\frac { 19 }{ 2 }\)
(D) None of these
Solution :
2 sin² 60° + 3 cot² 30° – tan 45°

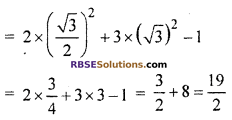
Hence, option (C) is correct.

Question 4.
If in ∆ABC, ∠C is right-angle, (RBSESolutions.com) then value of cos (∠A + ∠B) is :
(A) 0
(B) 1
(C) \(\frac { 1 }{ 2 }\)
(D) \(\frac { \sqrt { 3 } }{ 2 }\) [NCERT Exemplar Problem]
Solution :
Given : ∠C of ∆ABC is right angle.

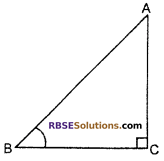
∵ We know that sum of all the three angles of a triangle is 180°.
∴ ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠B + 90° = 180°
⇒ ∠A + ∠B = 180° – 90°
⇒ ∠A + ∠B = 90°
Taking cos both sides.
⇒ cos (∠A + ∠B) = cos 90°
⇒ cos(∠A + ∠B) = 0
Hence, option (A) is correct.

Question 5.
If tan θ = √3, then value (RBSESolutions.com) of sin θ is :
(A) \(\frac { 1 }{ \sqrt { 3 } }\)
(B) \(\frac { \sqrt { 3 } }{ 2 }\)
(C) \(\frac { 2 }{ \sqrt { 3 } }\)
(D) 1
Solution :

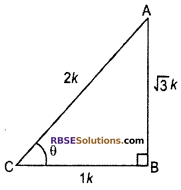
tan θ = \(\frac { AB }{ BC }\) = √3 = \(\frac { \sqrt { 3 } }{ 1 }\)
Let AB = √3 k
and BC = k
In right angled ∆ABC, by (RBSESolutions.com) pythagorus theorem,
AC² =AB² + BC²
= (√3k)² + (k)²
= 3k² + k² = 4k²
∴ AC = 2k
Now,

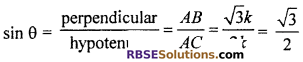
Hence, option (B) is correct.

Question 6.
sin (45° + θ) – cos (45° – θ) equals :
(A) 2 cos θ
(B) 0
(C) 2 sinθ
(D) 1 [NCERT Exemplar Problem]
Solution :
sin (45° + θ) – cos (45° – θ)
= sin (45° + θ) – cos [90° – (45° + θ)] [∵ (45° – θ) = {90° – (45° + θ)}]
= sin (45° + θ) – sin (45° + θ) [∵ cos (90° – θ) = sin θ]
= 0
Hence (B) is correct.

Question 7.
Given sin α = \(\frac { 1 }{ 2 }\) and cos β = \(\frac { 1 }{ 2 }\), then (RBSESolutions.com) value of (α + β) is :
(A) 0°
(B) 30°
(C) 60°
(D) 90° [NCERT Exemplar Problem]
Solution :
Given,
sin α = \(\frac { 1 }{ 2 }\) ⇒ sin α = sin 30°
α =30°
and cos β = \(\frac { 1 }{ 2 }\) ⇒ cos β = cos 60°
β = 60°
Now, α + β = 30° + 60° = 90°
Hence, option (D) is correct.

Question 8.
If tan θ = 1, then (RBSESolutions.com) cos θ will be :
(A) 1
(B) \(\frac { 1 }{ 2 }\)
(C) \(\frac { \sqrt { 3 } }{ 2 }\)
(D) \(\frac { 1 }{ \sqrt { 2 } }\)
Solution :
tan θ = 1
⇒ tan θ =tan
∴ θ = 45°

Hence, option (D) is correct.

Question 9.
If sec θ = √2, then (RBSESolutions.com) value of θ will be :
(A) \(\frac { \pi }{ 8 }\)
(B) \(\frac { \pi }{ 6 }\)
(C) \(\frac { \pi }{ 4 }\)
(D) \(\frac { \pi }{ 3 }\)
Solution :
sec θ = √2
sec θ = sec 45° = sec \(\frac { \pi }{ 4 }\)
θ = \(\frac { \pi }{ 4 }\)
Hence, option (C) is correct.

Question 10.
If θ = 30°, then \(\frac { { 1-sin }^{ 2 }2\theta }{ cos2\theta }\) is
(A) 1
(B) -1
(C) 2
(D) -2
Solution :


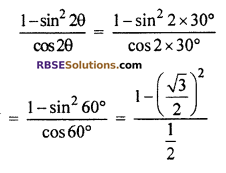
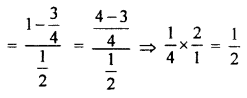
Hence, (RBSESolutions.com) option (B) is correct.

Short/Long Answer Type Questions

Question 1.
Evaluate : cosec² 30° – 3 sec 60°.
Solution :
cosec² 30° – 3 sec 60°
= (2)² – 3(2)
= 4 – 3 × 2 = 4 – 6
= -2

Question 2.
Evaluate : 4 cos³ 45° – 3 cos 45°
Solution :
4 cos³ 45° – 3 cos 45°

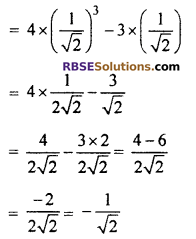
Question 3.
Find the value (RBSESolutions.com) of the following :
(i) sin 60° cos 30° + sin 30° cos 60°
(ii) 2 tan² 45° + cos² 30° – sin² 60°

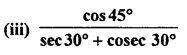
Solution :
(i) sin 60° cos 30° + sin 30° cos 60°

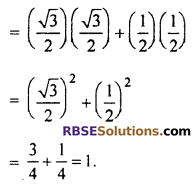
(ii) 2 tan² 45° + cos² 30° – sin² 60°

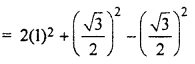
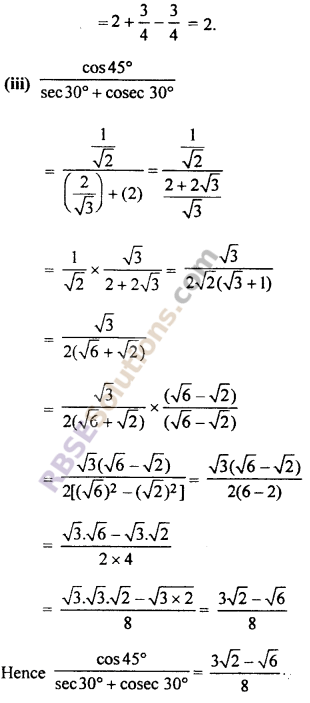
Question 4.
Prove (RBSESolutions.com) that : \(\frac { { sin60 }^{ \circ } }{ { 1+cos60 }^{ 0 } }\) = tan 30°
Solution :
L.H.S.= \(\frac { { sin60 }^{ \circ } }{ { 1+cos60 }^{ 0 } }\)

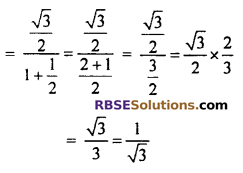
R.H.S. = tan 30° = \(\frac { 1 }{ \sqrt { 3 } }\)
Thus, L.H.S. = R.H.S.

Question 5.
Evaluate : 3 sin 60° – 4 sin³ 60°
Solution :
3 sin 60° – 4 sin³ 60°
Putting values of (RBSESolutions.com) trigonometric ratios

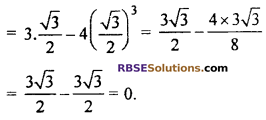
Question 6.
If tan 3x = sin 45° cos 45° + sin 30°, then find value of x.
Solution :
tan 3x = sin 45° cos 45° + sin 30°
⇒ tan 3x = \(\frac { 1 }{ \sqrt { 2 } }\) × \(\frac { 1 }{ \sqrt { 2 } }\) + \(\frac { 1 }{ 2 }\)
⇒ tan 3x = \(\frac { 1 }{ 2 }\) + \(\frac { 1 }{ 2 }\)
⇒ tan 3x = 1
⇒ tan 3x = tan 45°
⇒ 3x = 45°
⇒ x = 15°

Question 7.
If A = B = 60°, then (RBSESolutions.com) prove that :
(i) cos(A – B) = cos A cos B + sin A sin B
(ii) sin(A – B) = sin A cos B – cos A sin B
Solution :
(i) A = B = 60° (Given)
LH.S. cos(A – B) = cos(60° – 60°)
= cos 0° = 1
R.HS. cosA cosB + sinA sinB
= cos 60° cos 60° + sin 60° sin 60°
cos² 60° + sin² 60° = 1 [ sin² θ + cos² θ = 1]
Thus, L.H.S. R.H.S.
(ii) sin(A – B) = sin A cos B – cos A sin B
L.H.S. sin(A – B) = sin(60° – 60°)
= sin 0° = 0
R.H.S. sin A cos B – cos A sin B
= sin 60° cos 60° – cos 60° sin 60°
= 0
Thus, L.H.S. = R.H.S.

We hope the given RBSE Solutions for Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 6 Trigonometric Ratios Additional Questions, drop a comment below and we will get back to you at the earliest.