RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Additional Questions

RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Additional Questions is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Additional Questions.

Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Additional Questions

Multiple Choice Type Questions
Question 1.
If the height of a pole is 6 m and (RBSESolutions.com) the length of its shadow is 2√3 m, then the angle of elevation of sun is equal to :
(A) 60°
(B) 45°
(C) 30°
D) 90° [NCERT Exemplar Problem]
Solution :
Let AB is a pole of height 6 m
Length of a shadow of pole BC = 2√3 m
Let angle of elevation of sun ∠ACB = θ

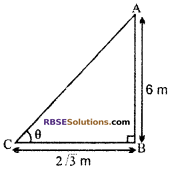
From right angled ΔABC,
tan θ = \(\frac { AB }{ BC }\)
⇒ tan θ = \(\frac { 6 }{ 2\sqrt { 3 } } \)
⇒ tan θ = √3
⇒ tan θ = tan 60°
⇒ θ = 60°
So, correct choice is (A).

Question 2.
A kite ¡s flying at a height of 30 m from the (RBSESolutions.com) ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is : [CBSE 2012]
(A) 45°
(B) 30°
(C) 60°
(D) 90°
Solution :
Let A is a kite which is 30 meter high from the ground which is flying with string of 60 m long.
Let ∠ACB = θ

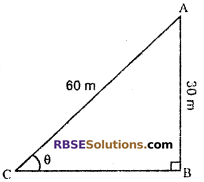
From right angled
sin θ = \(\frac { AB }{ AC }\)
⇒ sin θ = \(\frac { 30 }{ 60 }\)
⇒ sin θ = \(\frac { 1 }{ 2 }\)
⇒ sin θ = sin 30°
⇒ θ = 30°
So, correct choice is (B).

Question 3.
If the angle of elevation of a point at horizontal slope (RBSESolutions.com) of a hill is 60°. If one has to walk 300 m to reach to top of hill from the point then distance of the point from the foot of the hill :
(A) 300√3 m
(B) 150 m
(C) 150√3 m
(D) \(\frac { 150 }{ \sqrt { 3 } }\) m
Solution :
Let BC is a hill. Let AB = x m and length between A to C i.e., AC = 300 m and ∠BAC = 60°

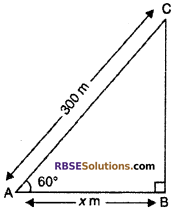
From right angled ΔABC
cos 60° = \(\frac { AB }{ AC }\)
⇒ \(\frac { 7 }{ 5 }\) = \(\frac { x }{ 300 }\)
⇒ x = \(\frac { 300 }{ 2 }\)
∴ x = 150 m
Hence, distance of point from base is 150 m.
So, correct choice is (B).

Question 4.
If angle of elevation of sum is 45° then the (RBSESolutions.com) length of the shadow casts by a 12 m high tree is :
(A) 6√3 m
(B) 12√3 m
(C) \(\frac { 12 }{ \sqrt { 3 } }\) m
(D) 12 m
Solution :
Let BC is a tree of height 12 m and shadow of tree AB = x m and angle of elevation of sun = 45°
i.e., ∠CAB = 45°

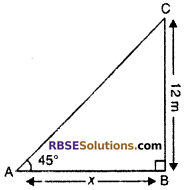
From right angled ΔABC,
tan 45° = \(\frac { BC }{ AB }\)
⇒ 1 = \(\frac { 12 }{ x }\)
x = 12 m
Hence, length of shadow of tree = 12 m
So, correct choice is (D).

Question 5.
A ladder ¡s placed against a wall such that it (RBSESolutions.com) just reaches the top of the wall. The foot of the ladder 1.5 m away from the wall and ladder ¡s inclined at an angle of 60° with the ground. Height of the wall is :
(A) 2.60 m
(B) 2.10 m
(C) 4.52 m
(D) 12.60 m
Solution :
Let PQ is a wall of height h. Let QR is ladder and QR = 1.5 m.
Since ladder makes an angle 60° with the ground i.e., ∠PRQ = 60°.

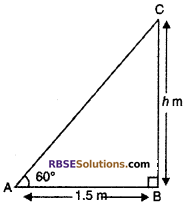
From right angled ΔPQR
tan 60° = \(\frac { PQ }{ QR }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ 1.5 }\)
h = 1.5 × √3
= 1.5 × 1.732 [∵ √3 = 1.732]
= 2.598 m
= 2.60 m
Hence, height of wall = 2.60 m
So, correct choice is (A)

Question 6.
If a length of a kite is 100 m which makes an (RBSESolutions.com) angle 60° from horizontal. Taking it as a straight line and its one end on the ground, then find the height of the kite from the ground :
(A) \(\frac { 100 }{ \sqrt { 3 } }\) m
(B) 50√3 m
(C) 25√3 m
(D) 100√3 m
Solution :
Let kite is at point P and height of kite from ground PR = h m.
Length of string of kite (PQ) = 100 m
Angle of string from horizontal ∠PQR = 60°

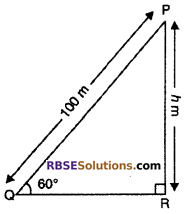
From right angled ∆PRQ,
sin 60° = \(\frac { PR }{ PQ }\)
⇒ \(\frac { \sqrt { 3 } }{ 2 } \) = \(\frac { h }{ 100 }\)
⇒ 2 × h = 100√3
⇒ h = \(\frac { 100\sqrt { 3 } }{ 2 }\)
∴ h = 50√3 m
Hence, height of kite from ground is 50√3 m
So, correct choice is (B).

Question 7.
If the shadow of a tree is times of its (RBSESolutions.com) height, then find the angle of elevation :
(A) 45°
(B) 60°
(C) 90°
(D) 30°
Solution :
Let PQ is a tree of height h m
Length of shadow of tree OQ = h√3 m
Let angle of elevation of sun is θ i.e., ∠POQ = θ

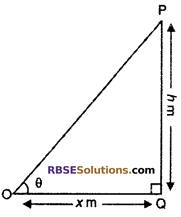
From right angled ∆OQP
tan θ = \(\frac { PQ }{ OQ }\)
⇒ tan θ = \(\frac { h }{ \sqrt { 3 } h } \)
⇒ tan θ = \(\frac { 1 }{ \sqrt { 3 } }\)
= tan 30°
∴ θ = 30°
So, angle of elevation of sun is 30°
So, correct choice is (D).

Question 8.
From the base of a tower a straight line is (RBSESolutions.com) at distance of 4 m and 16 m the angle of elevation of top of tower from two points are complementary, then height of tower is :
(A) 12 m
(B) 10 m
(C) 8 m
(D) 64 m
Solution :
If angle of elevations of top of tower from two points at straight line are complementary, then
Height of tower

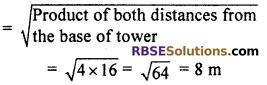
So, correct choice is (C).

Question 9.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. If the angle made by the rope with the ground level is 30°, then height of pole is :
(A) 10√3 m
(B) 10 m
(C) 20 m
(D) 20√3 m
Solution :
Let AB is a pole. Length of string is 20 m and angle (RBSESolutions.com) made by string with ground 30°
i.e., ∠ACB = 30°

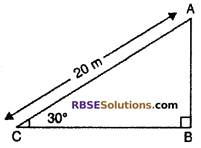
From right angled ∆ABC
sin 30° = \(\frac { AB }{ AC }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { AB }{ 20 }\)
∴ AB = \(\frac { 20 }{ 2 }\) = 10 m
Hence, height of pole = 10 m
So, correct choice is (B).

Question 10.
A house makes a right angle at the window of its opposite. Angle from horizontal to top is 60°. If the width of street is 6 m, then height of house is :
(A) 6√3 m
(B) 2√3 m
(C) 8√3 m
(D) 24 m
Solution :
Let C is window in the following figure (RBSESolutions.com) and AB is a house. House makes right angle from window C i.e.,
∠ACB = 90°

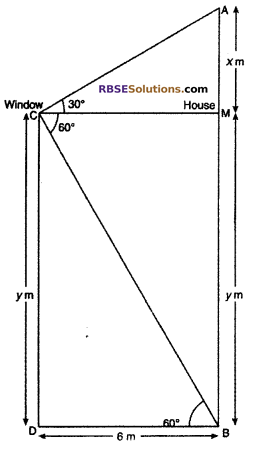
width of street BD = CM = 6 m
∠CBD = 60°, ∠ACM = 90° – 60° = 30°
Let AM = x and CD = BM = y
From right angled ∆CDB,
tan 60° = \(\frac { CD }{ BD }\)
\(\sqrt { 3 }\) = \(\frac { y }{ 6 }\)
or y = 6√3 m
From right angled ∆AMC,

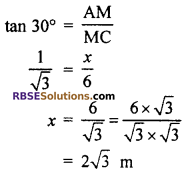
Hence, height of house = AB = AM + BM
= x + y
= 2√3 + 6√3
= 8√3 m
So, correct choice is (C).

Question 11.
A point is at 100 m distance from the base of a tree. (RBSESolutions.com) The angle of depression of the point from the top of the tree is 40°, then the height of the tree is :
(A) 100√2 m
(B) 100 m
(C) 50√2 m
(D) None of these
Solution :
Let height of tree AC is h m. From its ground C, point B is 100 m. The angle of depression of B from top of tree A is 45°.
So, ∠XAB = 45° = ∠ABC

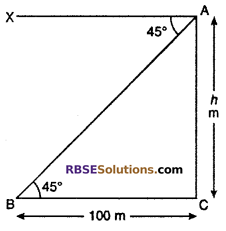
From right angled ∆ACB,
tan 45° = \(\frac { h }{ 100 }\)
⇒ 1 = \(\frac { h }{ 100 }\)
⇒ h = 100 m
So, correct choice is (B).

Question 12.
The top of a broken tree due to windstorm makes a 30° angle (RBSESolutions.com) and the top of the tree from the foot of the tree touches the ground at 15 m distance. The total height of the tree in m is :
(A) 15√2 m
(B) 15√3 m
(C) 30√3 m
(D) None of these
Solution :
Let length of tree before windstorm is AB. After windstorm the tree broken from point C reaches at point D on the ground which makes an angle 30°.

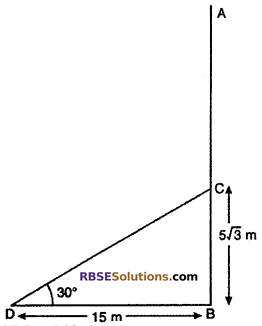
∠CDB = 30°, AC = CD and BD = 15 m
From right angled ∆DBC,


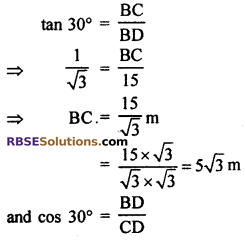
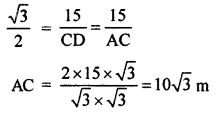
So, total length of tree
AB = AC + BC
= (10√3 + 5√3)m = 15√3 m
So, correct choice is (B).

Question 13.
From the top of a 200 m high pillar, the top and (RBSESolutions.com) foot of another pillar respectively of 30° and 60°, make an angle of elevation. The height of the second pillar and the distance between the two pillars is in m :

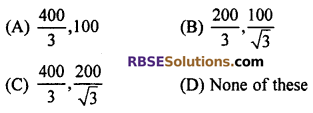
Solution: Let a pillar of height 200 m. The second pillar AB is x m distance from its of height h. An angle of A and B from top 300 and 60°.
Hence,
∠XPA = ∠PAM = 30°
∠XPB = ∠PBQ = 60°

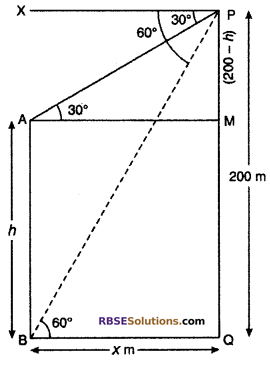
Let BQ = AM = x
AB = MQ = h
So, PM = PQ – MQ = (200 – h)m
From right angled ∆PQB,
tan 60° = \(\frac { PQ }{ BQ }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 200 }{ x }\)
⇒ x = \(\frac { 200 }{ \sqrt { 3 } }\) m
From right angled ∆PMA,

So, correct choice is (C).

Question 14.
The angles of elevation of a pillar from (RBSESolutions.com) point A and B are respectively 30° and 60°. If the distance between A and B is l, then the difference of point A and the foot of the pillar is :

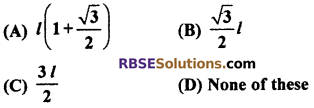
Solution :
Let PQ is pillar of height h. Let point B is at x distance from foot of pillar Q.
According to question,
∠PAQ = 30°, ∠PBQ = 60° and AB = l

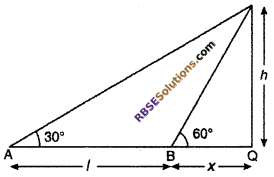
From right angled ΔPQB,
tan 60° = \(\frac { PQ }{ BQ }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ x }\)
⇒ h = √3 x …..(i)
From right angled ΔPQA,
tan 30° = \(\frac { PQ }{ AQ }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ l+x }\)
⇒ l + x = √3h
⇒ l + x = √3(√3x) [From equation (i) h = √3x]
⇒ l + x = 3x
⇒ 2x = l
⇒ x = l/2
Hence, distance between foot of pole and point A.
= AQ = AB + BQ
= l + x
= l + \(\frac { l }{ 2 }\) = \(\frac { 3l }{ 2 }\)
So, correct choice is (C).

Question 15.
A man stands at a point A of a 50√3 m high (RBSESolutions.com) tower at one side from that point that person sees the angle of elevation 30° of the top of the tower. On the other side of the tower some point is such as point A, tower and point B are linear and the distance of point A to point B is 200 m then the angle of elevation of the top of the tower from point B will be:
(A) 75°
(B) 60°
(C) 45°
(D) 30°

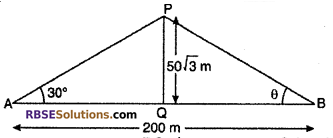
Solution :
Let PQ is a tower of height 50√3 m. The angle of (RBSESolutions.com) elevation of top of tower from A is 30°. One point B is at a distance 200 m from point A. Let angle of elevation of the top of tower from point B is θ.
From right angled ΔPQA,
tan 30° = \(\frac { PQ }{ AQ }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 50\sqrt { 3 } }{ AQ }\)
⇒ AQ = 50√3 × √3
= 150 m
QB = AB – AQ
= 200 – 150
= 50 m
From right angled ΔPQB,
tan θ = \(\frac { PQ }{ QB }\)
= \(\frac { 50\sqrt { 3 } }{ 50 }\) = \(\sqrt { 3 }\) = tan 60°
or θ = 60°
So, Correct choice is (B).

Question 16.
A men standing under a bridge measured the angle of (RBSESolutions.com) elevation of a ship coming from 100 m distance from him, send a message to the captain that the height of the ship Is 5 meter less from the bridge, hence the ship can pass without problem, but when the ship reaches at the bridge he found that the height of the ship in 68.2 m more then the bridge. what is the percentage of error in measuring the angle of elevation by the man. (√3 = 1.732) (CBSE 2012)
(A) 30%
(B) 25%
(C) 15%
(D) 5%
Solution :
Measuring angle = 45°

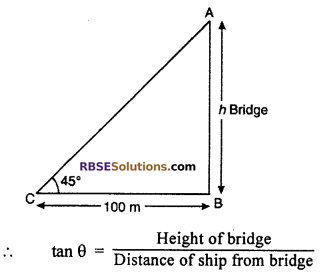
⇒ tan 45° = \(\frac { AB }{ BC }\)
l = \(\frac { h }{ 100 }\)
⇒ h = 100 m
Hence, actual height of ship = 100 + 5 + 68.2 = 173.2 m
If angle of elevation is α, then
tan α = \(\frac { 173.2 }{ 100 }\) = 1.732 = √3 = tan 60°
∴ α = 60°
∴ Error in measuring angle 60° – 45 = 15°
∴ Percentage error = \(\frac { 15\times 100 }{ 60 } \) = 25%
So, correct choice is (B).

Question 17.
The top of a tower makes angle a at one point which ¡s at its (RBSESolutions.com) foot and the other point which is high from the other point h m, the angle of depression of the base of the tower is β. The height of the tower is :
(A) h tan α
(B) h tan β
(C) \(\frac { htan\alpha }{ tan\beta } \)
(D) \(\frac { htan\beta }{ tan\alpha } \)
Solution :
Let BC is a tower of height H m. Let point A is at x distance from the base of tower such that angle of elevation of top of tower is α i.e.,
∠BAC = α

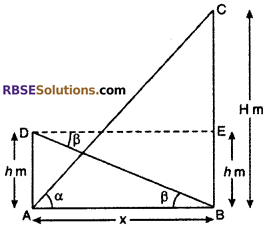
Let a point D is at height h from point A. The angle of (RBSESolutions.com) depression of the base of tower from point D is β. Then
∠EDB = ∠ABD = β (Alternate angle)
From right angled ∆BAD,
tan β = \(\frac { h }{ x }\)
or x = \(\frac { h }{ tan\beta } \) …..(i)
Again from right angled ΔABC,
tan α = \(\frac { BC }{ AB }\) = \(\frac { H }{ x }\)
or x = \(\frac { H }{ tan\alpha } \) ……(ii)
From equation (i) and (ii),
\(\frac { H }{ tan\alpha } \) = \(\frac { h }{ tan\beta } \)
or H = \(\frac { htan\alpha }{ tan\beta } \)
So, correct choice is (C).

Question 18.
The angle of depression of a boat from a 15 m high bridge (RBSESolutions.com) on a river is 30°. If the boat floats at a speed of 6 km/h then the
time taken by the boat to reach under the bridge will be:
(A) 15.59 sec.
(B) 13.62 sec.
(C) 90 sec.
(D) 18 sec.
Solution :
Let height of bridge is AB and C is a boat.
Given : AB = 15 m

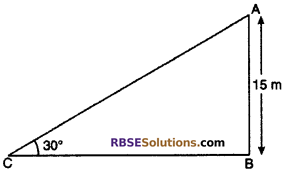
From right angled ΔABC
tan 30° = \(\frac { AB }{ BC }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 15 }{ BC }\)
⇒ BC = 15√3 m
Speed of boat = 6 km/h
= \(\frac { 6\times 1000 }{ 60\times 60 }\) m/sec
= \(\frac { 5 }{ 3 }\) m/sec
∴ Time taken to reach to bridge = \(\frac { Distance }{ Speed }\)
= \(\frac { 15\sqrt { 3 } \times 3 }{ 5 }\)
= 9√3 sec
= 9 × 1.732
= 15.588 sec
So, correct choice is (A).

Question 19.
The poles of two lamps are of equal height A boy (RBSESolutions.com) standing exactly at the mid of the poles finds its angle of elevation 45°. While moving 15 m towards one pole, he finds the angle of elevation of the top of that pole 60°. The height of the pole and the distance between them is approximately :
(A) 15 and 30 m
(B) 23.1 and 46.2 m
(C) 35.5 and 71 m
(D) 23.1 and 35.55 m
Solution :
Let two poles are AB and PQ of height h m. Distance between in these boles BQ = 2x. Point C is between these points which is mid-point of BQ.

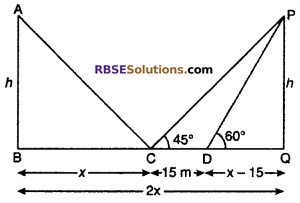
From ΔPQC, tan 45°= \(\frac { PQ }{ CQ }\)
⇒ l = \(\frac { h }{ x }\)
⇒ h = x …..(i)
The angle of elevation of top of pole from point D is 60°. This (RBSESolutions.com) point D is 15 m distance from point C in the side of pole. So that
DQ = CQ – CD = (x – 15)m
From right angled ΔPQD

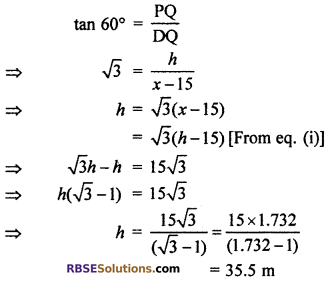
∴ Distance between points = 2x = 2h
= 2 × 35.5 = 71 m
So, correct choice is (C).

Very Short/Short Answer Type Questions

Question 1.
A man looks from the top of tower that the angle of depression of (RBSESolutions.com) a point of the earth is 60°. If the distance of the point is 25 m from the base of the tower, them find out the height of the tower.
Solution :
AB is a tower. The angle of depression of top of tower from point A to point C is 60°.
So ∠XAC = 60°
⇒ ∠ACB = 60°

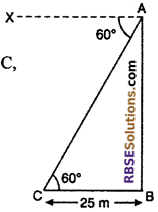
From right angled ΔABC,
tan 60° = \(\frac { AB }{ BC }\)
\(\sqrt { 3 }\) = \(\frac { AB }{ 25 }\)
Hence, height of tower = 25√3 m

Question 2.
One skyscraper is 100 dm. At some time the shadow of a 1 dm high pole is 3√3 dm (RBSESolutions.com) long from the light of the sun. What will be the angle of elevation of sun and the length of the shadow and the shadow of the skyscraper at the same time.
Solution :
Let BC is a skyscraper of height 100 dm. and DE is a pole of height 9 dm.
Let elevation angle of sun is θ.

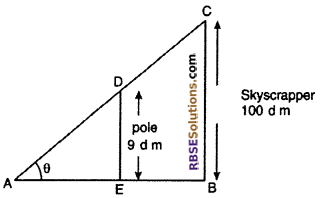
According to question, ∠DAE = ∠CAB = θ and AE = 3√3 dm
From right angled ΔDEA
tan θ = \(\frac { DE }{ AE }\)
= \(\frac { 9 }{ 3\sqrt { 3 } }\)
= √3
= tan 60° ⇒ θ = 60°
Hence, angle of elevation of sun = 60°
Again from right angled ΔABC,
tan θ = \(\frac { BC }{ AB }\)
⇒ tan 60° = \(\frac { 100 }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 100 }{ AB }\)
⇒ AB = \(\frac { 100 }{ \sqrt { 3 } }\)
Hence, angle of elevation of sun is 60° and length of shadow of skyscraper \(\frac { 100 }{ \sqrt { 3 } }\) decimeter

Question 3.
A light house which faces the north, throws light beam in (RBSESolutions.com) the shape of a fan from north-cart to north-west in the sky. On a ship a man that is going to west looks the light for the first time. When he is at 8 km distance from the light house and continuously looks it for 15√2 minutes then find out the speed of the ship in km/h.
Solution :
O is a light house which faces north. when ship reaches pint A then it looks light, where OA = 8 km. When the ship reaches at point B after 15√2 minutes, then it happens to see the light.

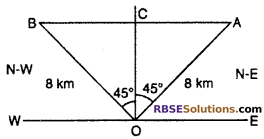
So, OB = OA = 8 km
From right angled ΔBCO.

Hence, speed of aeroplane = 30 km/h

Question 4.
The angle of depression of two consecutive (RBSESolutions.com) stones from a aeroplane are α and β. Prove that height of aeroplane is \(\frac { 1 }{ cot\alpha +cot\beta }\).
Solution :
Let two km stones are B and C for which distance between them 1 km i.e. BC = 1 km.
The angle of depression of B and C from A are α and β and plane is at h height from ground. So AD = h.

Question 5.
The distance of a point of top of a tower is 40 m which is (RBSESolutions.com) horizontally at the foot of the tower at 20 m. Find out the angle of elevation of the top of the tower from that point. Find out the height of the tower.
Solution :
Let height of tower AB = h m. Let angle of elevation is θ then,
Form right angled ΔABC,
cos θ = \(\frac { BC }{ AC }\)
= \(\frac { 20 }{ 40 }\) = \(\frac { 1 }{ 2 }\)
= cos 60°
or θ = 60°

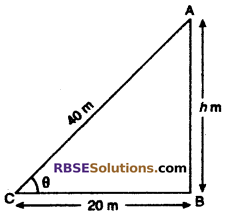
Again from right angled ΔABC,
tan θ = \(\frac { AB }{ BC }\)
tan 60° = \(\frac { h }{ 20 }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ 20 }\)
⇒ h = 20√3 m
Hence angle of elevation of top of tower is 60° and height of tower = 20√3 m.

Question 6.
An aeroplane flying at 1500 m height from the earth has angle of (RBSESolutions.com) elevation 60° from the airport. Fiad oat the horizontal distance of the aeroplane from the airport.
Solution :
Let horizontal distance of aeroplane from airport OQ = x m. Height of aeroplane QP = 1500 m and angle of elevation of aeroplane from airport = 60°

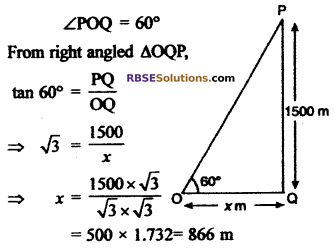
Hence, horizontal distance of plane from airport = 866 m.

Question 7.
A 2 meter long observer is at 28 meter distance from a tower. (RBSESolutions.com) The angle of elevation of top of tower from his eyes is 60°. Find the height of tower.
Solution :
Let AB a tower and CD is a observer. The distance between tower and observer = 28 m and angle of elevation is 60° i.e.,
BC = DE = 28 m
CD = BE =2 m and ∠ADE = 60°

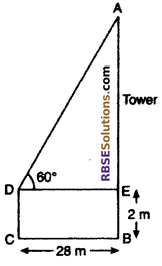
Form right angled ΔAED
tan 60° = \(\frac { AE }{ ED }\)
⇒ \(\sqrt { 3 }\) = \(\frac { AE }{ 28 }\)
⇒ AB = 28√3 m
= 28 × 1.732 = 48.496 m
Height of tower AB = BE + AE = 2 + 48.496
= 50.5 meter (approx)
Hence, height of tower is 50.5 m (approx)

Long Answer Type Questions
Question 1.
An aeroplane when flying at a height of 3000 m from the ground (RBSESolutions.com) passes vertically above another aeroplane at an instant when the angles of elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find first aeroplance is how much high with second aeroplane. (CBSE 2014)
Solution :
Let height of first aeroplane is BD which is flying at 3000 m height and height of second aeroplane BC = h m. Let angles of elevation from point A are 60° and 45° respectively. So,
∠BAD = 60° and ∠CAB = 45°and Let AB = x m.
From right angled ΔABD,
tan 60° = \(\frac { BD }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 3000 }{ x }\)

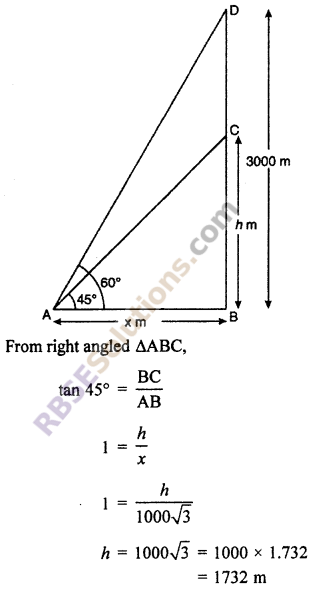
Hence, height of second plane from first plane
CD = BD – BC = 3000 – 1732 = 1268 m

Question 2.
If the angle of elevation top of point D of leaning tower at the (RBSESolutions.com) point A and B is α and β. If slope of tower is θ, then prove that
\(cot\theta =\frac { bcot\alpha -\alpha cot\beta }{ b-a } \)
Where a and b are the distances of A and B from tower (b > a).
Solution :
Let CD is a leaning tower and angles of elevations of top of point D at the place A and B are α and β.
So, ∠DBM = β, ∠DAM = α

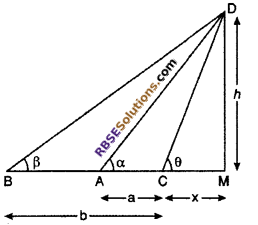
Let ∠DCM = θ and DM = h m, CM = x m and AC = a, BC = b.
From right angled ΔDMC,
tan θ = \(\frac { DM }{ CM }\)
⇒ tan θ = \(\frac { h }{ x }\)
⇒ x = \(\frac { h }{ tan\theta }\) = h cot θ ….(i)
From right angled ΔDMA,
tan α = \(\frac { DM }{ AM }\)
tan α = \(\frac { h }{ a+x }\)
⇒ a + x = \(\frac { h }{ tan\alpha }\) = h cot α
⇒ a = h cot α – x
= h cot α – h cot θ
= h[cot α – cot θ] ……(ii)
For right angled ∆DMB,
tan β = \(\frac { DM }{ BM }\)
cot β = \(\frac { BM }{ DM }\)
cot β = \(\frac { b+x }{ h }\)
b + x = h cot β
b = h cot β – x
b = h cot β – h cot θ
= h [cot β – cot θ] ……(iii)
Divide equation (iii) in equation (ii),
\(\frac { a }{ b }\) = \(\frac { h\left( cot\alpha -cot\theta \right) }{ h\left( cot\beta -cot\theta \right) }\)
⇒ a(cot β – cot θ) = b(cot α – cot θ)
⇒ (b – a)cot θ = b cot α – a cot β
⇒ \(cot\theta =\frac { bcot\alpha -\alpha cot\beta }{ b-a } \)

Question 3.
A round balloon of radius ‘r’ subtends an angle θ at the eye (RBSESolutions.com) of the observer, while angle of elevation of its center is ϕ. Find the height of the center of the balloon. (NCERT Exemplar Problem)
Solution :
Let center of balloon of radius r of O and A is the position of observer. let AP and AQ are too tangents to the balloon.
OB = h m

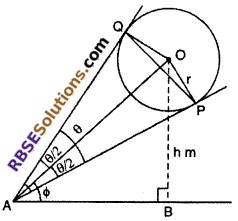
Balloon of radius r, subtends an angle θ and angle of (RBSESolutions.com) elevation of its center is ϕ. Then
∠PAQ = θ
and ∠PAO = ∠QAO = θ/2
OP = r and ∠PAB = ϕ
∠APO = ∠AQO = 90°
[∵ Radius and tangents are perpendicular to each other]
From right angled ∆OAB,
⇒ sin ϕ = \(\frac { OB }{ AO }\)
⇒ sin ϕ = \(\frac { h }{ AO }\)
⇒ h = AO sin ϕ ….(i)
From right angled ∆AOP,
sin \(\frac { \theta }{ 2 }\) = \(\frac { OP }{ AO }\)
⇒ sin \(\frac { \theta }{ 2 }\) = \(\frac { r }{ AO }\)
AO = r cosec \(\frac { \theta }{ 2 }\) ……(ii)
Put the value of AO in equation (i),
h = r cosec \(\frac { \theta }{ 2 }\) sin ϕ
Hence, height of the center of the balloon (h) = r cosec \(\frac { \theta }{ 2 }\) sin ϕ

Question 4.
A ladder rests against a wall at an angle a to the horizontal. (RBSESolutions.com) Its foot is pulled away from the B wall through a distance p, so that it slides a distance q down the wall making an angle β with the horizontal. Prove that :
\(\frac { p }{ q } =\frac { cos\beta -cos\alpha }{ sin\alpha -sin\beta }\) (NCERT Exemplar Problem)
Solution :
Let AB is a wall and AC is a ladder with length x. The foot of ladder is pulled through distance p so that it slides a distance q down the wall.

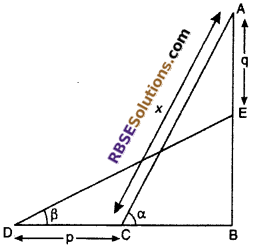
∠ACB = α and ∠EDB = β
From right angled ∆ABC,
sin α = \(\frac { AB }{ AC }\)
⇒ sin α = \(\frac { AB }{ x }\)
⇒ AB = x sin α …..(i)
and cos α = \(\frac { BC }{ AC }\)
⇒ cos α = \(\frac { BC }{ x }\)
⇒ BC = x cos α ….(ii)
BD = BC + CD
= x cos α + p
BE = AB – AE
= x sin α – q ….(iii)
From right angled ∆EBD,

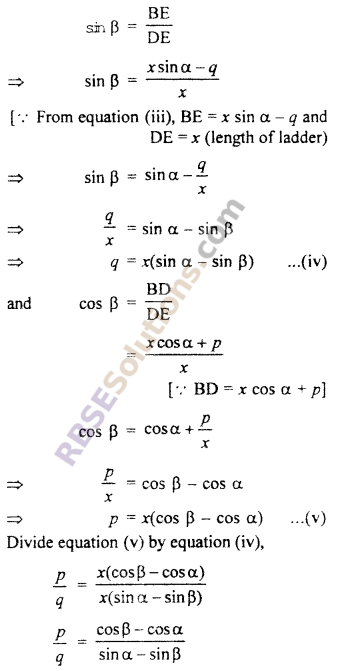
Question 5.
A window of a house is h m high above the ground. (RBSESolutions.com) The angle of elevation and depression of the top and the foot of another house on the opposite side of the street are a and respectively. Prove that height of another house is h(1 + tan α cot β) (NCERT Exemplar Problem)
Solution :
Let AB is a house and A be the window of the house,. then AB = h m

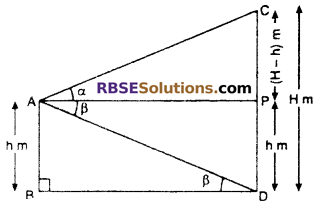
Let CD is a another house of height H meter then ∠ADB = ∠PAD = β (Alternate Angle)
From right angled ∆APC,

From right angled ∆ABD,

Put the value in equation (iii) from equation (i),
h cot β = (H – h) cot α
h cot β = H cot α – h cot α
⇒ h cot β + h cot α = H cot α

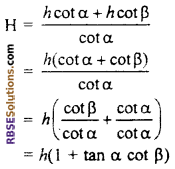
Hence, height of another house is h(1 + tan α cot β)m.

Question 6.
From the top of a tower 100 m high the angle of (RBSESolutions.com) elevation of the top of a hill is found to be 30°. From the bottom of this tower, the angle of elevation of the top of the hill is found to be 45°, then find the height of the hill
Solution :
Let AB is a tower of height 100 m and height of bill CD is h meter. The angle of elevation of hill from top of tower and bottom of tower is 30° and 45° respectively
i.e., ∠CAE = 30° and ∠CBD = 45°
AB = ED = 100 m
CE = CD – ED
= (h – 100)m
BD = x m (Let)

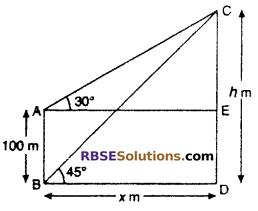
From right angled ∆CEA,

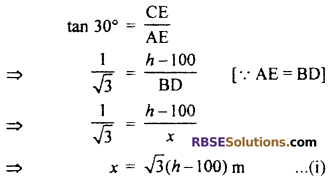
Again From right angled ∆CDB,
tan 45° = \(\frac { CD }{ BD }\)
l = \(\frac { h }{ x }\)
h = x m ….(ii)
Put the value of x from eq. (i) in eq. (ii),

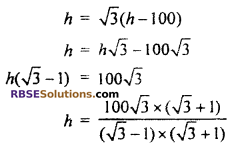
= 50(3 + 1.732)
= 50 × 4.73
= 236.5 m
Hence, height of hill = 236.5 m

Question 7.
If the angle of elevation of a cloud from a point h m (RBSESolutions.com) above a lake is α and the angle of depression of its reflection in the lake be β. Prove that the distance of the cloud from the point of observations is \(\frac { 2hsec\alpha }{ tan\beta -tan\alpha }\)
Solution :
Let LC is a surface of lake and D is a point of observation. A is the position of cloud.
The angle of elevation from point D is α.
Let AC = H

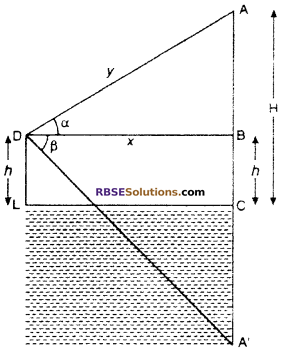
Again, let D = y, and DB = x. The angle of depression of shadow of cloud from point D is β.
Hence, ∠ADB = α and ∠BDA’ = β
From right angled ∆ABD,
tan α = \(\frac { AB }{ DB }\)
⇒ tan α = \(\frac { H-h }{ x }\)
⇒ H – h = x tan α
⇒ H = h + x tan α ….(i)
From right angled ∆A’BD,
tan β = \(\frac { { A }^{ \prime }B }{ DB }\)
⇒ tan β = \(\frac { H+h }{ x }\)
⇒ H + h = x tan β
Put the value of H from equation (i) in equation (ii),
h + x tan α + h = x tan β
⇒ x tan α + 2h = x tan β
⇒ 2h = x tan β – x tan α
⇒ 2h = x(tan β – tan α)
⇒ x = \(\frac { 2h }{ tan\beta -tan\alpha } \) ….(iii)
From right angled ∆ABD,
cos α = \(\frac { DB }{ AD }\)
= \(\frac { x }{ y }\)
y = \(cot\theta =\frac { x }{ cos\alpha } \)
= x sec α ……(iv)
Put the value of x from equation (iii) in equation (iv)
y = \(\frac { 2hsec\alpha }{ tan\beta -tan\alpha }\)
Hence, distance of cloud from the point of observation is \(\frac { 2hsec\alpha }{ tan\beta -tan\alpha }\).

Question 8.
From the top of hill which is 200 m high the angle of (RBSESolutions.com) depression of the top and the bottom of a pole are 300 and 60° respectively. Find the height of pole and its distance from the hill.
Solution :
Let CE is a pole of height h meter. AD is a hill of height 200 m. Let distance between bottom of hill to pole = x m.

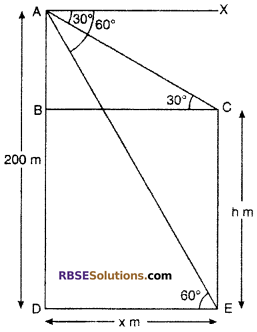
According to question ∠XAC= 30° = ∠ACB and ∠XAE = 60° = ∠AED
From right angled ∆ADE
tan 60° = \(\frac { AD }{ DE }\)
⇒ \(\sqrt { 81 }\) = \(\frac { 200 }{ x }\)
⇒ x = \(\frac { 200 }{ \sqrt { 3 } }\) m
From right angled ∆ABC,

Hence, height of pole = 133.33 m.

Question 9.
From the top of 60 m high building, the angle of elevation and (RBSESolutions.com) angle of depression of the top and bottom of a light house from top of building are 30° and 60° respectively. Find out
(i) Difference in heights of light house and building.
(ii) Distance between light house and building. (CBSE 2014)
Solution :
Let AB is a building of height 60 m and CD is a light house of height h m. The angle of elevation and angle of depression of the top and bottom of a light house from top of building are 30° and 60° respectively.
∠CAE = 30° and ∠EAD = 60°
∠ADB = ∠EAD = 60° (Alternate angle)
Draw BD || AE
∴ ∠AEC = 90° (Corresponding angle)
∠ABD + ∠BDE = 90° + 90° = 180°
∴ AB || DE
So, ABDE is a rectangle.
DE = AB = 60 m
and CE = (h – 60)m

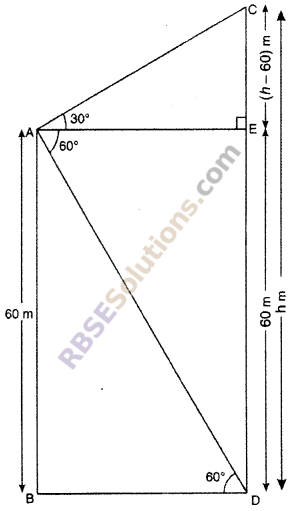
From right angled ∆AEC,
tan 30° = \(\frac { CE }{ AE }\)
\(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h-60 }{ BD }\) [∵ AE = BD]
⇒ BD = √3(h – 60)m …..(i)
From right angled ∆ABD,

Put the value in equation (ii) from equation. (i),
√3(h – 60) = 20 √3
⇒ h – 60 = \(\frac { 20\sqrt { 3 } }{ \sqrt { 3 } }\) = 20
⇒ h = 20 + 60 = 80 m
Hence, height of light house = 80 m
(i) Difference in height between light house and building
= 80 – 60 = 20 m
(ii) Distance between light house and building
BD = 20√3 m

Question 10.
A vertical tower stands on a horizontal plane and is (RBSESolutions.com) surmounted by a vertical flag-staff. At a point on the plane 9 m away from the tower, the angle of elevation of the top and the bottom of the flag-staff are respectively 60° and 30°. Find the height of the flag-staff and height of the tower. (CBSE 2013)
Solution :
Let AB is a flag-staff and BC is tower. Let AB = x m and BC =h m. A point D which is 9 m away from the foot of tower C on the plane. The angle of elevation of the top and the bottom of the flag-staff are 60° and 30° respectively. Hence ∠ADC = 60° and ∠BDC = 30°

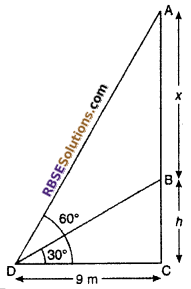
From right angled ∆BCD

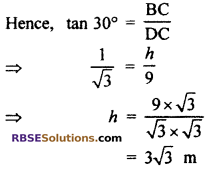
Hence, height of tower = 3√3 m
Again from right angled ∆ACD,
tan 60° = \(\frac { AC }{ DC }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h+x }{ 9 }\)
⇒ h + x = 9√3
⇒ 3√3 + x = 9√3
⇒ x = 9√3 – 3√3
= 6√3 m
∴ Hence, height of flag-staff in 6√3 m.

Question 11.
A vertical tower stands on a plane and is surmounted by a (RBSESolutions.com) pole of height 5 m. At a point A on the plane, the angle of elevation of the top of pole is 60° and the angle of depression of the point A from the top of tower is 45° Find the height of the tower. (CBSE 2011)
Solution :
BC is a tower of height h m. A pole CD is surmounted on this tower with height 5 m. Point A is x m away from the foot of the tower. Now,
∠DAB = 60° and ∠XCA = 45° = ∠CAB

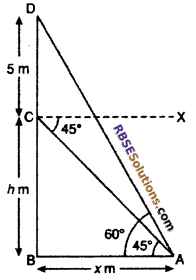
From right angled ∆ABC
tan 45° = \(\frac { BC }{ AB }\)
⇒ t = \(\frac { h }{ x }\)
⇒ h = x
From right angled ∆ABD,
tan 60° = \(\frac { BD }{ AB }\)

Hence, height of the tower = 6.83 m

Question 12.
The angle of elevation of the top of a tower from certain (RBSESolutions.com) point on horizontal plane is 30° If the observer moves 20 m towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower. (NCERT Exemplar Problem)
Solution :
Let AB is a tower of height h m. The angle of elevation of top of tower from point C is 30°. When moves 20 m towards the tower from point C, the angle of elevation increases 15°. i.e,
∠ACB = 30° and ∠ADB = 45°

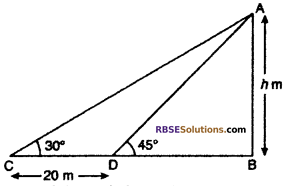
From right angled ∆ABD,
tan 45° = \(\frac { AB }{ BD }\)
⇒ l = \(\frac { h }{ BD }\)
⇒ BD = h m …(i)
From right angled ∆ABC,
tan 30° = \(\frac { AB }{ BC }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ 20+BD }\)

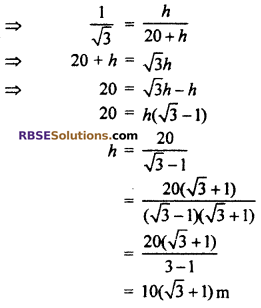
Hence, height of tower = 10(√3 + 1)m.

Question 13.
A tower in a city b 150 m high and a multistoreyed hotel at the (RBSESolutions.com) city center is 20 m high. The angle of elevation of the top of tower from the top of the hotel is 5°. A building, h m high is situated on the straight road connecting the tower with the city center at a distance of 1.2 km from the tower. If the top of the hotel, the top of the building and the top of the tower are in a straight line, then find the height of building h and distance of tower from the city center. (CBSE 2007)
(tan 5° = 0.0875, tan 85° = 11.43)
Solution :
Let AB is a tower of height AB = 150 m. CD is a building of height h m. and EF is a hotel of height EF = 20 m. Distance of building from tower BD = 1.2 km = 1200 m.

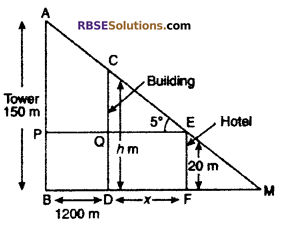
Let DF = x m
Given, ∠AEP = 5°
From figure PE = BF = (1200 + x)m
From right angled ∆APE

(1200 + x)(0.0875) = 130
⇒ 1200 × 0.0875 + 0.0875x = 130
⇒ 105 + 0.0875x = 130
⇒ 0.0875x = 130
⇒ 0.0875x = 130 – 105 = 25
⇒ x = \(\frac { 25 }{ 0.0875 }\)
= 286 m (approx)
x = DF = QE
Again from right angled ∆CQE
tan5° = \(\frac { CQ }{ QE }\)
CQ = QE tan 5°
= 286 × 0.0875
= 25.025 m
Hence, height of building h = CD
= QD + QC
= 20 + 25.025
= 45 m (approx.)
Distance of tower BF = BD + DE
= BD + QE [∵ DF = QE]
= 1200 + 286
= 1486 m
Hence, distance of tower from the city center = 1486 m.

Question 14.
The horizontal distance between two towers is 140 m. The angle (RBSESolutions.com) of elevation of the top of first tower when seen from the top of second tower is 30°. If the height of the second tower is 60 m then find the height of first tower.
Solution :
Let AB is a tower of height h and other tower is ED of height 60 m.
Distance between two towers EB = DC = 140 m

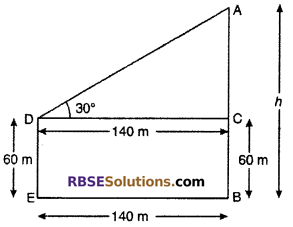
The angle of elevation of the top of first tower when seen from the top of second tower is 30°.
So, ∠ADC = 30°.
From right angled ∆ACD,

Hence, height of first tower = 140.8 m.

Question 15.
The angle of elevation of the top a cliff from a fixed (RBSESolutions.com) point A is θ. After going up a distance of K meters towards the top of the cliff at an angle of ϕ. It is found that the angle of elevation is α. show that the height of the cliff in meters is K

Solution :
Let CD is a hill. An angle of elevation at point A and B are ϕ, θ and α respectively.

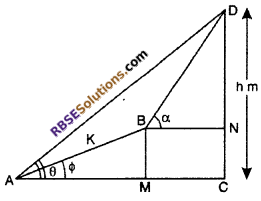
AB = K m
∠BAM = ϕ
∠DAC = θ and ∠DBN = α
Let CD = h m
From right angled ∆AMB
cos ϕ = \(\frac { AM }{ AB }\)
⇒ AM = AB cos ϕ = K cos ϕ …(i)
and sin ϕ = \(\frac { BM }{ AB }\)
⇒ BM = AB sin ϕ = K sin ϕ …(ii)
From right angled ∆ACD,
cos θ = \(\frac { AC }{ DC }\)
⇒ AC = DC cot θ = h cot θ …(iii)
∵ MC = AC – AM
From eq. (i) and (iii),
MC = h cot θ – K cos ϕ
∵ MC = BN
So, BN = h cot θ – K cos ϕ …..(iv)
From right angled ∆BND,
tan α = \(\frac { DN }{ BN }\)
⇒ DN = BN tan α
= MC tan α
= (h cot θ – K cos ϕ) tan α
h = DN + NC
= h cot θ tan α – K cos ϕ tan α + K sin ϕ
h[1 – cot θ tan α] = K[sin ϕ – cos ϕ tan α]

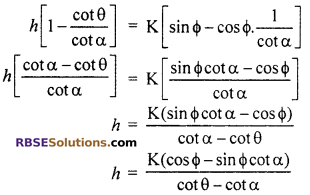
Question 16.
A boy standing on a horizontal plane finds a bird flying at a (RBSESolutions.com) distance of 100 m from him at an angle of elevation of 30°. A girl standing on the roof of 20 m high building. If the angle of elevation of the same bird to be 45°. Both the boy and the girl are opposite sides of the bird. Find the distance of the bird from the girl. (CBSE 2009)
Solution :
In the following figure let A, E and C are the position of bird, girl and boy respectively.
Now
∠ACB = 30°, ∠AED = 45°
AC = 100m and EF = 20 m

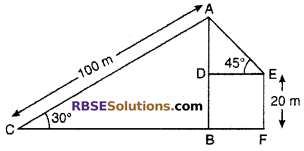
From right angled ∆ABC,
sin 30° = \(\frac { AB }{ AC }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { AB }{ 100 }\)
⇒ AB = \(\frac { 100 }{ 2 }\) = 50 m
⇒ AB =AD + BD
⇒ 50 = AD + 20 m
⇒ AD = 50 – 20 = 30m
From right angled ∆ADE,
sin 45° = \(\frac { AD }{ AE }\)
⇒ \(\frac { 1 }{ \sqrt { 2 } }\) = \(\frac { 30 }{ AE }\)
⇒ AE = 30√2 = 30 × 1.41
= 42.3 m
Hence, distance of bird from girl = 42.3 m

Question 17.
A contractor plans to install two slides for the children to (RBSESolutions.com) play in a park. For the children below the age of 5 years, she prefers to have a slide shows top is at a height of 1.5 m and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3 m, and inclined at an angle of 60° to the ground. What should be length of the slide In each case?
Solution :
Case I When contractor installs slide for children below the age of 5 years then its height AB = 1.5 m and ∠ACB = 30°
Let length of slide AC = x m

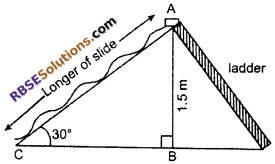
From right angled ∆ABC
sin 30° = \(\frac { AB }{ AC }\)
⇒ \(\frac { 1 }{ 2 }\) = \(\frac { 1.5 }{ x }\)
⇒ x = 1.5 × 2
∴ AC = 3 m
Case II. When contractor installs slide for children above (RBSESolutions.com) the age of 5 years then its height PQ = 3 m and ∠PRQ = 60°

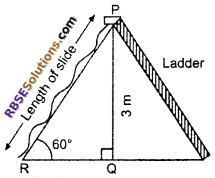
Let length of slide PR = y m
From right angled ∆PQR

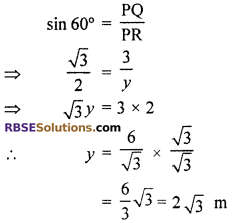
Hence, length of slide for children below the age of 5 years = 3 m and above the age of 5 years = 2√3 m.

Question 18.
A 1.2 m tall girl spots a balloon moving with the wind in a (RBSESolutions.com) horizontal line at a height of 88.2 m from the ground. The angle f elevation of the balloon from the eyes of the girl at any instant is 60°. After some time the angle of elevation reduces to 30° (see fig.). Find the distance traveled by the balloon during the interval.

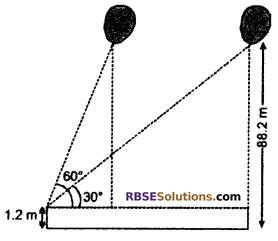
Solution :
Let eye of 1.2 m tall girl is A. The balloon flying 88.2 m height from (RBSESolutions.com) ground level have angle of elevation at different distances are 60° and 30° respectively.
∴ ∠BAE = 60° and ∠DAC = 30°
BE = CD = 88.2 – 1.2 = 87 m

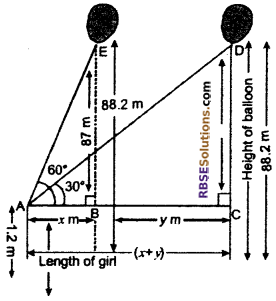
From right angled ∆ABE
tan 60° = \(\frac { BE }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 87 }{ x }\)
⇒ x = \(\frac { 87 }{ \sqrt { 3 } }\) ……(i)
From right angled ∆ACD
tan 30° = \(\frac { CD }{ AC }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 87 }{ x+y }\)
⇒ x + y = 87 √3
⇒ x = 87√3 – y ….(ii)
From equation (i) and (ii)

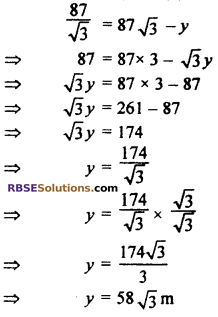
Hence, distance traveled by balloon = 58√3 m

Question 19.
The angle of elevation of an aeroplane from a point on the (RBSESolutions.com) ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the plane b flying at a constant height of 1500√3 m. Find the speed of the plane. (CBSE 2008)
Solution :
Let P and Q are the two position of plane and A is a observation point. Let ABC is a horizontal line from A. The angle of elevation of P and Q from A are 60° and 30° respectively. Now
∠PAC = 60°
∠QAC = 30°
and PB = QC = 1500√3 m

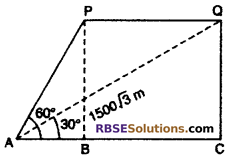
From right angled ∆PBA,
tan 60° = \(\frac { PB }{ AB }\)
⇒ \(\sqrt { 3 }\) = \(\frac { 1500\sqrt { 3 } }{ AB }\)
AB = 1500 m
From right angled ∆ACQ,
tan 30° = \(\frac { QC }{ AC }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { 1500\sqrt { 3 } }{ AB }\)
⇒ AC = 1500 × √3 × √3
= 4500 m
Now, PQ = BC
= AC – AB
= 4500 – 1500
= 3000 m
Hence, plane covers 3000 m distance in 15 seconds.
So, speed of plane = \(\frac { 3000 }{ 15 }\)
= 200 m/sec
= \(\frac { 200\times 60\times 60 }{ 1000 } \)
= 720 km/h

Question 20.
The angle of elevation of a plane from a point (RBSESolutions.com) A on the ground is 60°. After 10 seconds, the angle of elevation changes to 30°. If the plane is flying with speed 648 km/h, then find the height at which the plane is flying.
Solution :
Let plane is flying at height h, then
AQ = BR = h m

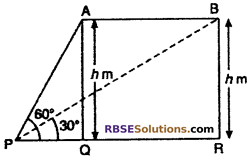
Speed of plane 648 km/h
= \(\frac { 648\times 1000 }{ 60\times 60 } \) m/sec
= 180 m/sec
Hence, distance covered in 1 sec by plane = 180 m
∴ So, distance covered in 10 sec,
= 180 × 10 = 1800 m.
Hence, AB = QR = 1800 m
Since, plane reaches B from A in 10 seconds.
Hence, angle of elevation (RBSESolutions.com) changes 30° to 60° from P.
So, ∠APQ = 60°, ∠BPR = 30°
From right angled ∆AQP
tan 60° = \(\frac { AQ }{ PQ }\)
⇒ \(\sqrt { 3 }\) = \(\frac { h }{ PQ }\)
⇒ PQ = \(\frac { h }{ \sqrt { 3 } }\) ….(i)
From right angled ∆BRP,
tan 30° = \(\frac { BR }{ PR }\)
⇒ \(\frac { 1 }{ \sqrt { 3 } }\) = \(\frac { h }{ PR }\)
⇒ PR = h√3 …..(ii)
∵ PR = PQ + QR
⇒ QR = PR – PQ
= h√3 – \(\frac { h }{ \sqrt { 3 } }\)
From equation (i) and (ii)
But QR = 1800 m

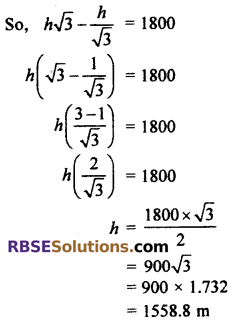
Hence, plane is (RBSESolutions.com) flying 1558.8 m height.

We hope the given RBSE Solutions for Class 10 Maths Chapter 8 Height and Distance Additional Questions will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 8 Height and Distance Additional Questions, drop a comment below and we will get back to you at the earliest.