RBSE Solutions for Class 10 Maths Chapter 9 Co-ordinate Geometry Ex 9.2

RBSE Solutions for Class 10 Maths Chapter 9 Co-ordinate Geometry Ex 9.2 is part of RBSE Solutions for Class 10 Maths. Here we have given Rajasthan Board RBSE Class 10 Maths Chapter 9 Co-ordinate Geometry Exercise 9.2.

Rajasthan Board RBSE Class 10 Maths Chapter 9 Co-ordinate Geometry Ex 9.2

Ex 9.2 Class 10 RBSE Question 1.
Find the co-ordinates of the point which divides the line (RBSESolutions.com) segment joining the points (3, 5) and (7, 9) in the ratio 2 : 3 internally.
Solution :
Let point P(x, y) divides the line segment joining the point A(3, 5) and B(7, 9) internally in the ratio 2 : 3.

Hence, the coordinate of P is \(\left( 4\frac { 3 }{ 5 } ,6\frac { 3 }{ 5 } \right) \).

Exercise 9.2 Class 10 RBSE Question 2.
Find the co-ordinates of the point which (RBSESolutions.com) divides the line segment joining the points (5, -2) and \(\left( -1\frac { 1 }{ 2 } ,4 \right) \) in the ratio 7 : 9 externally.
Solution :
Let point P(x, y) divides the line segment joining the points A(5, -2) and B\(\left( -1\frac { 1 }{ 2 } ,4 \right) \) externaly in the ratio 7 : 9.
x₁ = 5      y₁ = -2         m₁ = 7
x₂ = -1\(\frac { 1 }{ 2 }\)    y₂ = 4    m₂ = 9
By formula of external division

Hence, the coordinate of P is \(\left( 27\frac { 3 }{ 4 } ,-23 \right) \)

Class 10 Maths Ex 9.2 Solutions Question 3.
Prove that origin O divides the line joining (RBSESolutions.com) the points 4(1, -3) and B(-3, 9) in the ratio 1 : 3 internally. Find the co-ordinates of the points which externally divides the line.
Solution :
Let the point P(x, y) divides the line segment joining the point A(1, -3) and B(-3, 9) internally in the ratio 1 : 3.


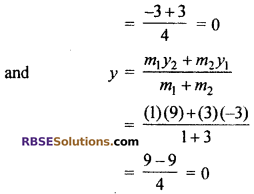
Hence co-ordinate of P(x, y) is (0, 0). So origin O is divides (RBSESolutions.com) the line segment joining the given points internally in the ratio 1 : 3.
Again point P(x, y) divides externally, then by formula of external division

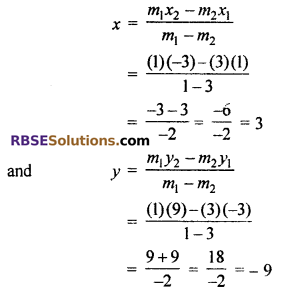
Hence, co-ordinate of point P which divides externally = (3, -9).

RBSE Solutions For Class 10 Maths Chapter 9 Question 4.
Find the mid point of line joining (RBSESolutions.com) the points (22, 20) and (0, 16).
Solution :
Let co-ordinates of mid point is P (x, y) which ¡s line joining the points A(22, 20) and B(0, 16).
x₁ = 22, y₁ = 20,  x₂ = 0, y₂ = 16
By formula of mid point

Hence, co-ordinate of mid point P(x, y) = (11, 18)

RBSE Solutions For Class 10 Maths Chapter 9.2 Question 5.
In which ratio, x-axis divides the line segment (RBSESolutions.com) which joins points (5, 3) and (-3, -2)?
Solution :
On x-axis, the ordinate of each point is zero. So let point P(x, 0) divides the line segment joining the points A(5, 3) and B(-3, -2) internally in the ratio m₁ : m₂

Hence, line segment joining the given points by x-axis divides internally in the ratio 3 : 2.

RBSE Class 10 Maths Chapter 9 Question 6.
In which ratio, y-axis, divides the line (RBSESolutions.com) segment which joins points (2, -3) and (5, 6)?
Solution :
On y-axis, coordinate of point x is zero, so let point P(0, y) divides the line segment joining the point A(2, -3) and B(5, 6) externally in the ratio m₁ : m₂.
Then by formula of external division

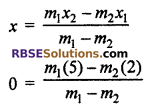
⇒ 5m₁ – 2m₂ = 0
⇒ 5m₁ = 2m₂
⇒ \(\frac { { m }_{ 1 } }{ { m }_{ 2 } } =\frac { 2 }{ 5 } \)
⇒ m₁ : m₂ = 2 : 5
Hence, line segment joining these points divides externally in the ratio 2 : 5 by y-axis.

Chapter 9 Maths Class 10 RBSE Solutions Question 7.
In which ratio, point (11, 15) divides the (RBSESolutions.com) line segment which joins (15, 5) and (9, 20)?
Solution :
Let the point P(1 1, 15) divides the line segment joining the point A(15, 5) and B(9, 20) internally in the ratio λ : 1
Hence x₁ = 15    y₁ = 5         m₁ = λ
x₂ = 9      y₂ = 20       m₂ = 1

⇒ 11(λ + 1) = 9λ + 15
⇒ 11λ + 11 = 9λ + 15
⇒ 11λ – 9λ = 15 – 11
⇒ 2λ = 4
λ = \(\frac { 4 }{ 2 }\) = \(\frac { 2 }{ 1 }\)
∴ λ : 1 = 2 : 1
Hence, required ratio is 2 : 1.

RBSE Class 10 Chapter 9 Question 8.
If point P (3, 5) divides line segment which (RBSESolutions.com) joins A(-2, 3) and B(x, y) in the ratio 4 : 7 internally, then find the co-ordinates of B.
Solution :
Let the coordinate of point B is (x, y)

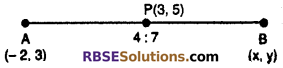
Let the point P(3, 5) divides the line segment joining the points A(-2, 3) and B(x, y) internally in the inthe ratio 4 : 7.
So, x₁ = -2,     y₁ = 3       m₁ = 4
x₂ = x       y₂ = y        m₂ = 7
By section formula


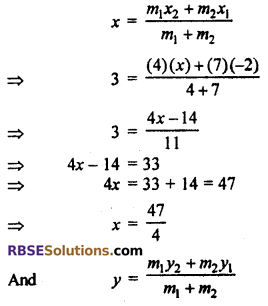
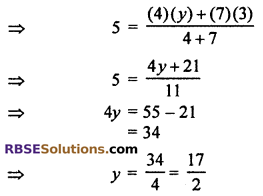
Hence, the co-ordinate of point B is \(\left( \frac { 47 }{ 4 } ,\frac { 17 }{ 2 } \right)\)

Ch 9 Class 10 Maths RBSE Question 9.
Find the co-ordinates of point which (RBSESolutions.com) trisects the line joining point (11, 9) and (1, 2).
Solution :
Let P(x₁ y₁) and Q(x₂, y₂) are required points which is trisect the line segment joining the points A(11, 9) and B(1, 2) respectively.
Let AP = PQ = BQ = x
PB = x + x = 2x
AQ = x + x = 2x

Hence point P divides line segment AB in the (RBSESolutions.com) ratio 1 : 2 and point Q, divides the line segment Ab in the ratio 2 : 1.
By the section formula for point P,
m₁ = 1, m₂ = 2

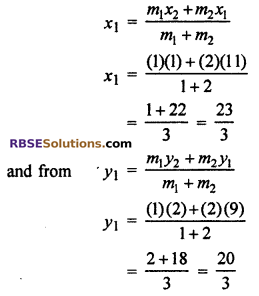
∴ Hence the co-ordinate of point P is \(\left( \frac { 23 }{ 3 } ,\frac { 20 }{ 3 } \right)\)
for point Q,
m₁ = 2, m₂ = 1

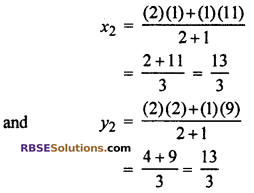
So, the co-ordinate of Q = \(\left( \frac { 13 }{ 3 } ,\frac { 13 }{ 3 } \right)\)
Hence, required coordinate of point P and Q is \(\left( \frac { 23 }{ 3 } ,\frac { 20 }{ 3 } \right)\) and \(\left( \frac { 13 }{ 3 } ,\frac { 13 }{ 3 } \right)\) respectively.

Coordinate Geometry Class 10 RBSE Question 10.
Find the co-ordinates of point which quarter (RBSESolutions.com) sects the line joining point (-4, 0) and (0, 6).
Solution :
Let C, D and E are required point which quarter sects the line segment joining the points A(-4, 0) and B(0, 6)

Since D is mid point of A and B, C is is midpoint A and D, and E ¡s mid point of D and B, then AC = CD = DE = EB
Now, co-ordinate of mid point D of A and B.

= \(\left( \frac { -2 }{ 2 } ,\frac { 9 }{ 2 } \right)\)
= \(\left( -1,\frac { 9 }{ 2 } \right)\)
Hence, co-ordinate of points divided in four equal (RBSESolutions.com) part of AB are \(\left( -3,\frac { 3 }{ 2 } \right)\), (-2, 3) and \(\left( -1,\frac { 9 }{ 2 } \right)\) respectively.

Chapter 9 Class 10 Maths RBSE Question 11.
Find the ratio in which line 3x + y = 9 divides the line segment which joins points (1, 3) and (2, 7)
Solution :
Let the line 3x + y = 9 divides the line segment joining A(1, 3) and B(2, 7) at point P(x, y) in the ratio λ : 1
x₁ = 1     y ₁ = 3     m₁ = λ
x₂ = 2     y₂ = 7      m₂ = 1

⇒ 6λ + 3 + 7λ + 3 = 9(λ + 1)
⇒ 13λ + 6 = 9λ + 9
⇒ 13λ – 9λ = 9 – 6
⇒ 4λ = 3
⇒ λ = \(\frac { 3 }{ 4 }\)
λ : 1 = 3 : 4
Hence, required ratio is 3 : 4.

RBSE Class 10 Maths Chapter 9.2 Question 12.
Find the ratio where point (-3, P), divides internally (RBSESolutions.com) the line segment which joins points (-5, -4) and (-2, 3). Also find P.
Solution :

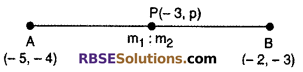
Let the point P(-3, p) divides the line segment joining the points A(-5, -4) and B(-2, 3) internally in the ratio m₁ : m₂.
Hence, x co-ordinate of point P(-3, p)

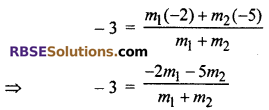
= -3(m₁ + m₂) = -2m₁ – 5m₂
⇒ -3m₁ – 3m₂ = -2m₁ – 5m₂
⇒ -3m₁ + 2m₁ = -5m₂ + 3m₂
⇒ – m₁ = -2m₂
⇒ \(\frac { { m }_{ 1 } }{ { m }_{ 2 } } =\frac { -2 }{ -1 } \) = \(\frac { 2 }{ 1 }\)
Hence required ratio m₁ : m₂ = 2 : 1
Now, y co-ordinate of point P(-3, p)

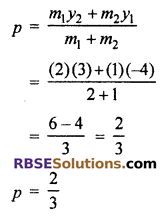
Hence, required (RBSESolutions.com) ratio 2 : 1 and p = \(\frac { 2 }{ 3 }\)

We hope the given RBSE Solutions for Class 10 Maths Chapter 9 Co-ordinate Geometry Ex 9.2 will help you. If you have any query regarding Rajasthan Board RBSE Class 10 Maths Chapter 9 Co-ordinate Geometry Exercise 9.2, drop a comment below and we will get back to you at the earliest.