RBSE Solutions for Class 11 Chemistry Chapter 2 Atomic Structure

Rajasthan Board RBSE Class 11 Chemistry Chapter 2 Atomic Structure

RBSE Class 11 Chemistry Chapter 2 Text Book Questions

RBSE Class 11 Chemistry Chapter 2 Multiple Choice Questions

Question 1.
If atomic number of an element is 25 and .its atomic mass is 55, then its nucleus contains:
(a) 25 protons and 30 neutrons
(b) 55 protons
(c) 30 protons and 25 neutrons
(d) 55 neutrons
Answer:
(a) 25 protons and 30 neutrons

Question 2.
H-spectrums shows :
(a) Diffraction
(b) Polarization
(c) Quantized Energy Levels
(d) Heisenberg Uncertainty Principle
Answer:
(c) Quantized Energy Levels

Question 3.
Energy of a photon is calculated by:
(a) E = hv
(b) h = Ev
(c) h = E/λ
(d) E = nλ
Answer:
(a) E = hv

Question 5.
In a sub shell of an atom, maximum number of electrons can be defined by which of the following?
(a) 4l + 2
(b) 2l + 1
(c) n²
(d) 2n²
Answer:
(d) 2n²

RBSE Class 11 Chemistry Chapter 2 Very Short Answer Type Questions

Question 6.
Calculate the number of protons in 34 mg, NH₃ at N.T.P.
Answer:
1 mol of NH₃ = 17g
1 mole of NH₃ = 6.023 × 10²³ molecules of NH₃
or, 1 atom of NH₃ contains = 10 protons
Number of proton in 1 mole NH₃ = 10 × 6.023 × 10²³ protons
Therefore 34 mg NH₃ = 6.023 x 1024 × 34/17 × 1000 = 1.2046 × 10²² protons.

Question 7.
Calculate the number of electrons in one mole Methane.
Answer:
1 molecule of CH₄ contains electron = 10
Therefore 1 mole (6.023 x 10²³ atoms) contains electron = 6.023 × 10²⁴

Question 8.
Out of 4f and 4d which orbital will experience high effective nuclear charge?
Answer:
Nuclear charge is defined as the net positive charge experienced by an electron in the orbital of a multi electron atom. The closer the orbital the greater is the nuclear charge experienced by the electron in it. 4d will experience greater nuclear charge than 4f as 4d is closer to the nucleus.

Question 9.
For n = 4 and ms = -1/2 orbital, how many electrons are present?
Answer:
Number of orbital in the nth shell = n²
For n = 4
Number of orbitals = 16
If each orbital is taken fully then, it will have 1 electron with ms value of -1/2 and one with 1/2.
Hence number of electrons with m_s value of (-1/2) is 16 i.e, half the total number of electrons.

Question 10.
Calculate the number of unpaired electrons in Fe and Cr.
Answer:
Fe is Iron and atomic number is = 26
The electronic configuration is: 1s², 2s², 2p⁶, 3s², 3p⁶, 4s², 3d⁶
Thus, It has 4 unpaired electrons.
Cr is a chromium and atomic no is 24 .
The electronic configuration of Cr is : 1s², 2s², 2p⁶, 3s², 3p⁶, 4s¹, 3d⁵.
Thus, chromium have 6 unpaired electrons.

Question 11.
The energy of electrons in an orbital depends on which of the quantum number?
Answer:
The energy of electrons in an orbital depends on principal quantum number.

Question 12.
Identify the period of the elements which belongs to the following electronic configuration: 1s² 2s² 2p⁶ 3s¹.
Answer:
The above electronic configuration shows that in element the last electron enters the s orbital having (the principal quantum number 3. Thus the element belongs to 3 period.

Question 13.
Calculate the number of electrons in 1 gm atomic mass.
Answer:
Mass of one electron = 9.10939 × 10^-31kg
Number of electron that weight 9.10939 × 10^-31 kg = 1
Number of electron that will weight 1g or (1 × 10^-3 kg)
= 0.1098 × 10^-3+31
= 0.1098 × 10²⁸
= 1.098 × 10²⁷
The number of electron in 1 gm atomic mass is 1.098 × 10²⁷

Question 14.
Determine the charges of 1 mole electrons
Answer:
Charge on 1 electron = 1.6022 × 10^-19C
Charge on 1 mole of electrons = (1.6022 × 10^-19) (6.023 × 10²³) = 9.65 × 10⁴ C
The charge of 1 mole electrons is 9.65 × 10⁴ Coulomb.

Question 15.
The wavelength of yellow light emitted by a sodium lamp is 580 nm. Calculate its frequency.
Answer:
We know that, the relation between wavelength and frequency is given by,
\(\lambda=\frac{c}{v}\)
or,
\(v=\frac{c}{\lambda}\)
Where v = frequency of light
c = velocity of light in vaccum = 3 × 10⁸ m/s
λ = wavelength of yellow light = 580 × 10^-9 m (Given)
Substituting the values, we get
v = \(\frac{3 \times 10^{8}}{580 \times 10^{-9}}\)
= 5.17 × 10¹⁴s^-1

Question 16.
Calculate the number of protons and electrons in the following: \(^{13} \mathrm{C}_{6},^{16} \mathrm{O}_{8},^{24} \mathrm{Mg}_{12},^{56} \mathrm{Fe}_{26}\).
Answer:
Atomic number = number of protons
For a neutral atom, Number of protons = number of electrons
For ¹³O₈
Mass number of carbon = 13
Atomic number = Number of protons = 6
Number of electrons = 6
For ¹⁶O₈
Mass number of Oxygen = 16
Atomic number of Oxygen = 8
Therefore, Number of protons and electrons = 8
For ²⁴Mg₁₂
Mass number of Magnesium = 24
Atomic number of Magnesium = 12
Therefore, Number of protons and electrons = 12

Mass number of Iron = 56
Atomic number of Iron = 26
Therefore, Number of protons and electrons = 26

Question 17.
Identify the orbitals for the following quantum numbers:
n = 1 l = 0 n = 2, l = 1
n = 4, l = 3 n = 3, l = 2
Answer:
For n = 1, l = 0, Is orbital
For, n = 2, l = 1, 2p
For, n = 4, l = 3, 4f orbitals
For, n = 3, l = 2, 3d orbital

Question 18.
Calculate number of electrons in \(\mathrm{H}_{2}^{+}, \mathrm{O}_{2}^{+}\) and H₂.
Answer:
Atomic number of H is 1. Therefore number of electron in H is 1.
For \(\mathrm{H}_{2}^{+}\), the number of electrons = 2
For \(\mathrm{H}_{2}^{+}\), it has positive charge which shows that one electron is missing
Therefore, number of electron in \(\mathrm{H}_{2}^{+}\) is 1.
Similarly, number of electrons in Oxygen is 8 (At. no. of O is 8)
In O₂, number of electrons = 16
In, \(\mathrm{O}_{2}^{+}\) it has one positive charge i.e., one electron less.
Therefore, \(\mathrm{O}_{2}^{+}\), has 15 electrons.

Question 19.
Who discovered protons and neutrons?
Answer:
Proton is discovered by Goldstein and James Chadwick discovered neutrons

Question 20.
What are the fundamental particles?
Answer:
The fundamental particles are electron, proton, and neutron.

RBSE Class 11 Chemistry Chapter 2 Short Answer Type Questions

Question 21.
Calculate radius of fifth Bohr orbital of hydrogen
Answer:
Radius of Bohr’s nth orbit for hydrogen atom is given by,
r_n = (0.0529 nm) n²
For,
n = 5
r₅ = (0.0529 nm) (5)²
r₅ = 1.3225 nm
Radius of fifth Bohr orbital of hydrogen is 1.3225nm.

Question 22.
If an electron jump from n = 3 to n = 2, then how much energy is emitted?
Answer:
Energy emitted is given by:
∆E = R_H(1/n₁² – 1/n₂²)
= 2.18 × 10^-18(1/3² – 1/2²)
= 2.18 × 10^-18(1/9 – 1/4)
= 2.18 × 10^-18(0.138)
= -10.9 × 10^-18 = -3.008 × 10^-19 J
or, 3.008 × 10^-19J × 1 ev/1.602 × 10^-19J × eV = -1.9 eV

Question 23.
What will be the angular momentum of an electron is 5th energy state, according to Bohr’s model?
Answer:
The angular momentum of electron in the orbit is equal to nh/2π,
Where n is the no of orbits,
So angular momentum of electron in 5th orbit is 5h/2π. Which is equal to 2.5h/π,
Hence the answer is 2.5h/π.

Question 24.
De broglie wavelength of an object having mass achy and moving with velocity 100 ms^-1 is 6.62 × 10^-35 m. Find the value of x
Answer:
Velocity (V) = 100 ms^-1
Mass(m) = x kg
Wavelength (λ) = 6.62 × 10^-35 m
Plank Constant (h) = 6.6 × 10^-34 Js

Question 25.
If uncertainty in momentum of an electron is 1 × 10^-5 kg ms^-1, then what will be the uncertainity in position?
Answer:
According to Heisenberg’s equation :
∆x × ∆p = \(\frac{h}{4 \pi}\)
Uncertainity in position,
= 6.63 × 10^-34/ 4 × 3.14 × (1 × 10^-5)
= 5.28 × 10^-30 m

Question 26.
Write the electronic configuration of Chromium in Free State
Answer:
The atomic number of chromium Cr = 24.
The electronic configuration is 1s², 2s², 2p⁶, 3s², 3p⁶, 4s¹, 3d⁵.

Question 27.
Calculate the value of all four quantum numbers for valence electron of rubidium, (Z = 37)
Answer:
Electronic configuration of Rb = 1s², 2s², 2p⁶, 3s², 3s²4s²3d¹⁰,4p⁶ 5s¹.
The outer electronic configuration is ns¹, for the 5th period n = 5 hence Principal quantum number, n = 5
Azimuthual quantum number, l = 0 (s orbital l = 0)
Magnetic quantum number m = 0 (l = 0, there is only one m value i.e. 0)
Spin quantum number, s = +1/2 or – 1/2 (there is only one electron and it can have clockwise or anticlockwise spins).
The four quantum number of Rb is 5, 0, 0, +1/2.

Question 28.
Which property is depicted by three quantum number n, l and m?
Answer:

• The first quantum number describes the electronic shell, or energy level, of an atom. Principal quantum number (n) describes the energy of an electron and the probable distances of the electron from the nucleus. The principal quantum number designates the principal electron shell.
• The angular quantum number (l) : The second quantum number, known as the angular or orbital quantum number, describes the sub-shell and gives the magnitude of the orbital angular momentum.
• Magnetic quantum number (m) describes the orbital in a sub shell.

Question 29.
Which elements contain six unpaired electrons according to Hund’s Rules?
Answer:
According to Hund’s rules, one electron is added to the each degenerate orbital in a sub-shell before two electrons can be added to the same orbitals in a sub-shell.

Chromium has six unpaired electrons, out of which 5 unpaired electrons are in the 3d orbitals and one unpaired electron is in the 4s orbital. Atomic number of Cr is = 24
Electronic configuration is: 1s², 2s², 2p⁶, 3s², 3p⁶, 4s¹, 3d⁵
Cr = 3d⁵, 4s¹

Question 30.
What will be the orbital angular momentum for d-electron?
Answer:
The orbital angular momentum (L) = \(\sqrt{(l(l+1))}\)h/2π
= √6h/ 2π (l = 2 for d-orbital)

Question 31.
Calculate number of electrons, protons and neutrons in element ⁸⁹Y_39.
Answer:
For given element atomic number is 39 and mass number is 89.
Now,
Atomic number = number of proton = 39
Number of electrons = Number of protons = 39
Number of neutrons = mass number – atomic number
= 89 – 39 = 50

Question 32.
What will be the ratio between areas covered by first and second orbits?
Answer:

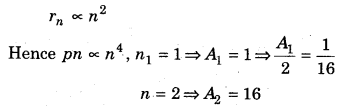
Question 33.
What is the reason of presence of three unpaired electrons in N-atom?
Answer:
The atomic number of Nitrogen is 7 and its electronic configuration is 1s², 2s², 2p^3-.

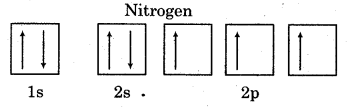
Arrangement of electrons in a sub-shell of an atom is given by Hund’s rule which states that pairing of electron in the orbitals of same sub-shell will not take place until all the orbitals are singly filled. Thus, according to the rule, the pairing of electrons in orbitals of 2p does not start in N because out of 5 electrons, 2 electrons go to 2s and 3 electrons are singly occupied in 2p sub-shell. Thus, there are 3 unpaired electrons in Nitrogen.

Question 34.
Determine the number of radial nodes of 3s and 2p orbitals.
Answer:
The radial nodes = n – l – 1
In 3s orbital n = 3, l = 0,
3s orbitals radial nodes = 3 – 0 – 1 = 2
2p orbital n = 2, l = 1,
Radial nodes of 2p orbital = 2 – 1 – 1 = 0,
Number of radial nodes of 3s and 2p orbital is 2, 0.

Question 35.
If (n + l) = 6, then what will be the possible number of the sub-shells?
Answer:
It is given that, the value of n + l = 6,
then n + 1 = 6
6 + 0 = 6
5 + 1 = 6
4 + 2 = 6
All above can be possible as values of ‘n’ are greater than the values of ‘l’. But, if the values of n are less than l, then other combination would be

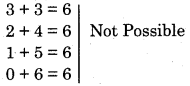
3 + 3 not possible as value of l = (n – 1 ). Hence total number of sub-shells would be 3.

RBSE Class 11 Chemistry Chapter 2 Long Answer Type Questions

Question 36.
Write the postulates of Bohr’s Model. What are the demerits of the Bohr’s Model?
Answer:
Bohr’s Atomic
Bohr (1913) gave an atomic model based on the study of Plank’s quantum theory and Radiation which over come, the short comings of Rutherfords atomic model and explains the general characters of structure and spectrum of hydrogen atom. Indeed, following two points were important for development of this model
(a) Dual nature of electro magnetic radiation
(b) Experimental observations of atomic spectrum indicate the electrons are quantized in atom

Neils Bohr (1913) was the first to explain quantitatively the general features of hydrogen atom structure and its spectrum. On the basis of Planck’s quantum theory, Bohr’s gave following assumptions.
1. In hydrogen atom electron revolves around nucleus in closed circular orbit.
2. There are various closed circular orbits around the nucleus that revolves only such orbits in which the angular momentum of electron is
integral multiple of \(\frac{h}{2 \pi}\)
\(m v r=\frac{n h}{2 \pi}\)
3. Each circular orbit possess a certain energy level, so there orbits are also known as energy level. Since in these orbits energy of revolving electron in constant so these are also known as stationary orbits. These orbits are denoted by K L M N or 1, 2,3,4.
4. The energy of orbit does not change with time but when an electron jumps to high or low level then it absorbs or emits the necessary amount of energy. This energy change is not continuous
5. During the transmission between two states absorbed or emitted radiation is given by following expression.

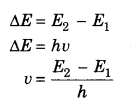
Where E₂ and E₁ are higher and lower energy states. This equation is known as law of Bohr’s frequency.
6. For revolving electron centrifugal force is equal to centripetal force.

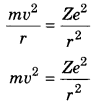
Where Z = Atomic number, m = mass of electron
v = Velocity of electron, e- charge of electron
r = distance of electron from nucleus (atomic radius)

Question 37.
Explain Planck’s Quantum theory.
Answer:
Particle Nature of Electromagnetic Radiation (Plank’s Quantum Theory)

German scientist. Max Plank (1900) propounded quantum theory of radiation. The main point of this theory are
1. Radiation energy could not emit or absorb consistently but it could emit or absorb in discrete quantities. These small bundles of energy are called quanta in terms of light these bundles are referred as ‘photon’
2. The energy (E) of each quanta is proportional to its frequency, i.e.,

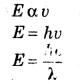
Where E = Energy
h = Plank’s constant
(6.62 × 10^-34 JS)
c = Speed of light
λ = Wave length
3. The total amount of energy emit or absorb by any particle is multiple or whole number of quatai
i. e., E = n hv
(Where ‘n’ is whole number, n – 1, 2, 3….. )

Question 38.
What is Rutherford’s Atomic Model? What are the reasons of failure?
Answer:
Rutherford’s Nuclear Model of Atom
Rutherford’s nuclear model of atom is given as follow

1. Atom is very small, spherical and electrically neutral particle containing maximum, empty part.
2. In an atom, the entire mass and positive charge is concentrated in a very small region at the centre, known as nucleus.
3. The nucleus of atom is positive because all positive charge of atom i.e, all protons are situated in nucleus.
4. Atom is electrically neutral. Hence number of proton present in atom in equal to the number of electron present in atom.
5. The circular path in which electron move around the nucleus is called orbit
6. The positively charged nucleus imposes attraction force on electron but it does not fall into nucleus because the centrifugal force produced by rotation of electron balance the attraction force of nucleus. Size of nucleus is very small as compared to size of atom. Nucleus is about 10^-15 th part of atom and its radius is proportion to cubic root of nucleons (proton + neutron) present in atom
   

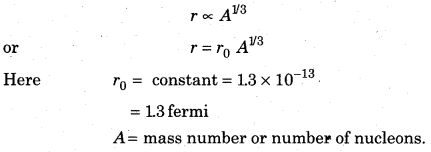
Limitations of Rutherford’s Model
The coulomb force between nucleus and electron is equal to gravitalional force in mathmatical form.

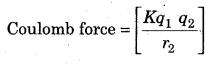
where q₁ and q₂ are charges
r is distance between q₁ and q₂
K is proportionality constant
The Rutherford model of atom resembles the solar system in which planets rotate around sun. But there are some short comings in this model, these are given as-

1. It was not able to explain the stability of atom.
2. It does not explain the spectrum of hydrogen and other atoms.
3. This model could not explain the distribution of electron.
   
4. 

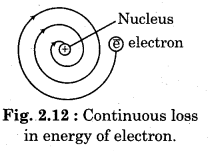
Question 39.
Write short notes on:
(a) Dual nature of Particle de-Broglie Hypothesis
(b) Heisenberg’s Uncertainty Principle
(c) Quantum number and Orbitals
(d) Shapes and Orbitals
Answer:
(a) Dual Nature of Particle de-Broglie Hypothesis : In 1924, Louis de Broglie suggested that matter exhibit dual behaviour i.e. both particle and wave nature. This means that it has both momentum and wavelength. According to de Broglie, the wavelength associated with a particle of mass ‘m’, moving with a velocity ‘v’ is given by equation:
λ = h/mv where h = Planck’s constant
This equation is applicable to all material objects but it has significance only in case of microscopic particles. According to Planck’s quantum theory.
E = hv or hc/λ
Where h = Plank’s constant, v = frequency of wave According to Einstein equation.
E = mc²
Where, m = mass of photon c = velocity of light, Equating both, we get,
hv = mc² but v = c/λ
hc/λ = mc² or λ = \(=\frac{h}{m c} \text { or } \lambda=\frac{h}{m v}\)
The above equation is de Broglie equation.

(b) Heisenberg Uncertainty principle: This principle was given by Werner Heisenberg in 1927. It states that “it is not possible to measure simultaneously both the position and momentum of microscopic particle” , Mathematically it is given as :

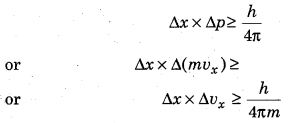
(c) Quantum number and orbitals : Quantum numbers are a set of four numbers with the help of which we can get complete information about all the electrons in an atom, i.e. location, energy, the type of orbital occupied, shape and orientation of that orbital. There are 4 quantum numbers:

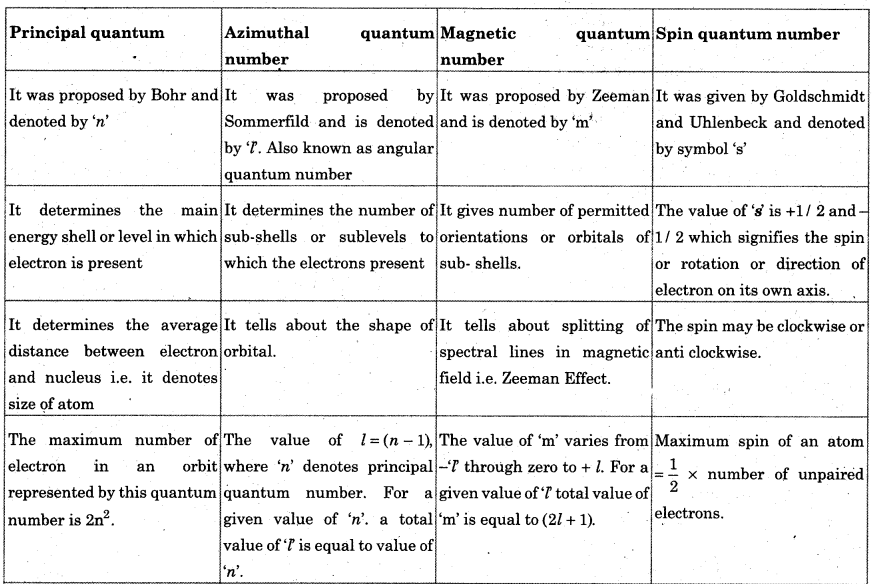
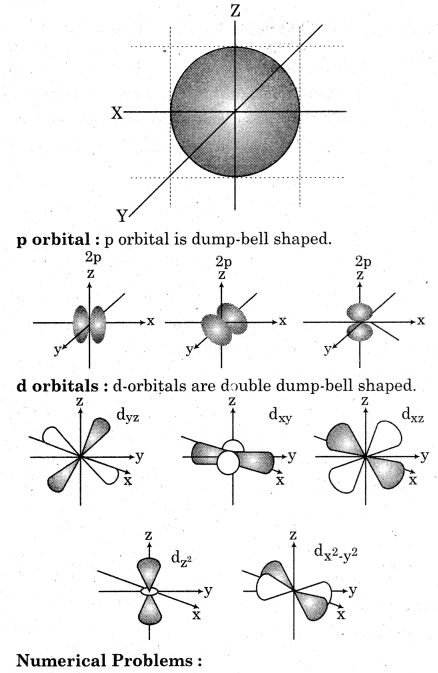
(d) Shapes and Orbitals
An orbital is a mathematical function that describes the wavelike behavior of an electron, electron pair, or nucleons. An orbital may also be called an atomic orbital or electron orbital. There are four orbital s, p, d and f. s orbitals : An s orbital is spherically symmetric around the nucleus of the atom, like a hollow ball made of rather fluffy material with the nucleus at its centre.

RBSE Class 11 Chemistry Chapter 2 Numerical Problems

Question 40.
The wavelength of yellow light emitted by sodium lamp is 580 nm. Calculate its frequency and wave number (v)
Answer:
We know that, the relation between wavelength and frequency is given by,

Where, v = frequency of light
c = velocity of light in vacuum 3 × 10⁸ m/s
λ = wavelength of yellow light = 580 nm = 580 × 10^-9 m (Given)
Substituting the values, we get.
v = 3 × 10⁸ m/s/580 × 10^-9 m
= 5.17 × 10¹⁴s^-1
Now, wave number of yellow light is given as,
\(\overline{v}=\frac{1}{\lambda}\)
= 1/580 × 10^-9 m
= 1.72 × 10^-6 m^-1

Question 41.
Calculate the energy of photon of light having frequency 3 × 10¹⁵ Hz. If the wavelength of the light is (0.50 Å), then calculate its energy.
Answer:
(i) Energy (E) of a photon is given by the expression,
E = hv
Where, h = Planck’s constant = 6.626 × 10^-34 Js
v = frequency of light = 3 × 10¹⁵ Hz (Given) Substituting the values we get,
E = (6.626 × 10^-34) × (3 × 10¹⁵)
E = 1.988 × 10^-18 J

(ii) Energy (E) of a photon having wavelength (λ) is given by the expression,
Where, E = \(\frac{h c}{\lambda}\)
h = Planck’s constant = 6.626 × 10^-34 Js
c = velocity of light in vacuum = 3 × 10⁸ m/sec
X = wavelength = 0.50 A or 0.50 × 10^-10 m
Substituting values in expression we get,
= 6.626 × 10^-34 × 3 × 10⁸/ 0.50 × 10^-10
= 3.98 × 10^-15 J

Question 42.
The work function of the metal is 2.13 eV. A photon having wavelength of 4 × 10^-7m strikes the metal then calculate kinetic energy of emission of energy of photon and velocity of photoelectron.
Answer:
(i) Energy (E) of a photon = hv
= hc/λ
Where, h = Planck’s constant = 6.626 × 10^-34 J sec
c = velocity of light in vacuum = 3 × 10⁸ m/s
λ = wave length of photon = 4 × 10^-7 m
Substituting the values, we get,
E = (6.626 × 10³⁴ )(3 × 10⁸)/(4 × 10^-7)
= 4.965 × 10^-19 J
Hence, the energy of the photon is 4.97 × 10^-19 J.

(ii) Kinetic energy of the emission = hv – hv_o
= (E – W)
= (4.97 × 10^-19 /1.6020 × 10^-19) eV – 2.13 eV
= (3.1020 – 2.13)eV
= 0.97 eV
Hence, the kinetic energy of emission is 0.97 eV.

(iii) The velocity of a photoelectron (v) can be calculated by the expression,

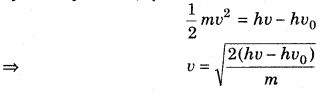
where (hv – hv_o) is kinetic energy of emission in Joules and ‘m’ is the mass of the photoelectron.
Substituting the values in the given expression of v :

Hence, the velocity of the photoelectron is 5.84 × 10⁵ ms^-1

Question 43.
A bulb of 25 W emits yellow colour monochromatic light of wavelength 0.57 m. Calculate number of photon emmited per second
Answer:
Power of bulb, P = 25 Watt = 25 Js^-1
Energy of one photon, E = hv = hc/λ.
Where ,
c = velocity of light in vacuum = 3 × 10⁸ m/s
h = Planck’s constant = 6.626 × 10^-34 Js
λ = 0.57 × 10^-6 m
Substituting the values, we get,
E = (6.626 × 10^-34) (3 × 10⁸)/ 0.57 × 10^-6
= 34.87 × 10^-20 J
Rate of emission of photon per second = 25/ 34.87 × 10^-20 = 7.169 × 10^-19 photon per second

Question 44.
When radiation of 6800 A wavelength strikes in metal surface, the electron with zero velocity emitted. Calculate the threshold frequency and work function (W_o) of the metal
Answer:
Threshold wavelength of radiation
(λ_o) = 6800 × 10^-10 m Or 6.8 × 10^-7
Threshold frequency of the metal (v_o) = c/λ_o
= (3 × 10⁸)/(6.8 × 10^-7)
v_o = 441 × 10¹⁴ s^-1
Now,
work function (W_o) of the metal = hv_o
= (6.626 × 10^-34 JS)(441 × 10¹⁴S^-1)
= 2.922 × 10^-19 J

Question 45.
If an electron of hydrogen atom jumps from n = 4 to n = 2 energy state, which wavelength of light will be emitted?
Answer:
The transition from n_i = 4 to an energy level with n_f = 2, will give rise to a spectral line of the Balmer series. The energy involved in the transition is given by the relation,

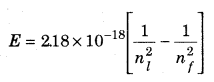
Solving the equation we get,
E = 2.18 × 10^-18 [(1/4²) — (1/2²)]
= 2.18 × 10^-18 [1-4/16)]
= 2.18 × 10¹⁸ [-3/16]
or, E = -(4.0875 × 10^-19 J)
The negative sign indicates that the energy is emitted during the transition. Now, the wavelength of transmission is given by the expression,
λ = hc/E
where c = velocity of light in vaccum = 3 × 10⁸ m/s
h = Planck’s constant = 6.626 × 10^-34 J sec
Substituting the values we get,
λ = (6626 × 10^-34) (3 × 10⁸) / (-40875 × 10^-19)
= 486 × 10⁷m
or, λ = 486 nm

Question 46.
If the value of energy of 1st orbit of hydrogen atom is -2.18 × 10¹⁸ J atm^-1, then what will be energy associated with 5th orbit?
Answer:
Energy associated with the fifth orbit of hydrogen atom can be calculated as:
E_n = (2.18 × 10^-18)Z² / n²
E₅ = (2.18 × 10^-18)1² / 5²
E₅ = -8.72 × 10^-20 J

Question 47.
Calculate the wavelength of electron if it is moving with a velocity of 2.05 × 107 ms^-1.
Answer:
According to de Broglie’s equation,
λ = h/mv
Where, λ = wavelength of moving particle
m = mass of particle (9.109 × 10^-31 Kg)
v = velocity of particle (2.05 × 10⁷ ms^-1)
h = Planck’s constant (6.626 × 10^-34)Js
Substituting the values in the expression of A:
X = (6626 × 10^-34 Js) / (9.109 × 10^-31)(2.05 × 10⁷ ms^-1)
= 3.54 × 10^-11 m
Hence, the wavelength of the electron is 3.54 × 10^-11 m.

Question 48.
Calculate the minimum amount of energy required to remove an electron from n = 2 completely. For hydrogen, the energy of electron is E = -2.18 × 10^-18 /n²J. Calculate longest wavelength of light which can be used in the above transition.
Answer:
Given that the electron energy in hydrogen atom
E_n = (-2.18 × 10^-18)/n²J
Energy required for ionization from n = 2 is given by
∆E = E_∞ – E₁
= [0- [(2.18 × 10^-18)/ 4] J
= 0.545 × 10¹⁸ J
∆E = 5.45 × 10^-19 J
Now, λ = he/∆E
= (6.626 × 10^-34) (3 × 10⁸)/ 5.45 × 10^-19
= 3647 × 10^-10 m
= 3647 Å

RBSE Solutions for Class 11 Chemistry