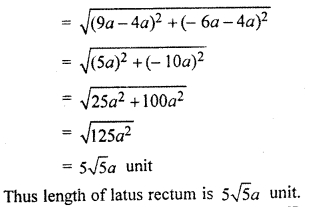RBSE Solutions for Class 11 Maths Chapter 12 Conic Section Ex 12.4

Rajasthan Board RBSE Class 11 Maths Chapter 12 Conic Section Ex 12.4

Question 1.
Find the coordinates of the points of intersection where straight line 4y + 3x + 6 = 0 cuts the parabola 2y2 = 9x.
Solution:
Equation of straight line,
4y + 3x + 6 = 0
⇒ 3x = -4y – 6 …(i)
Equation of parabola,
2y² = 9x …(ii)
From eqⁿ. (i) and (ii),
2y² = 3(-4y – 6)
⇒ 2y² = – 12y – 18
⇒ 2y² + 12y + 18 = 0
⇒ y² ± 6y + 9 = 0
⇒ (y + 3)² = 0 ⇒ y = -3
Putting y = – 3 in eqⁿ. (ii),
9x = 2 × (-3)² = 2 × 9
⇒ x = 2
Thus coordinates of intersection point of (2, – 3).

Question 2.
Find the length of chord cut by line 4y – 8 at parabola y² = 8x.
Solution:
Equation of parabola,
y² = 8x …(i)
Equation of line,
4y – 3x = 8
⇒ 4y = 3x + 8

Thus, coordinates of ends of chord are (8,8) and (\(\frac { 8 }{ 9 } \),\(\frac { 8 }{ 3 } \)) Thus, length of chord

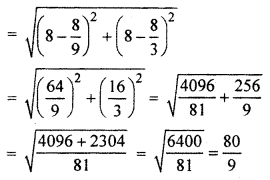
Thus, length of chord is \(\frac { 80 }{ 9 } \) units.

Question 3.
Prove that straight line x + y = 1 touches parabola y = x – x².
Solution:
Equation of parabola,
y = x – x² …(i)
Equation of straight line,
x + y = 1 …(ii)
On solving eq. (i) and (ii),
⇒ x + x – x² = 1
⇒ x² – 2x + 1 = 0
This is a quadratic equation, its roots will be equal and coincide
⇒ B² – 4AC = 0
⇒ (- 2)² – 4(1) (1) = 0
⇒ 4 – 4 = 0
⇒ 0 = 0
Hence, straight line x + y = 1 will touch the parabola
y = x – x².

Question 4.
Find the condition that line lx + my + n = 0 touches the parabola y² = 4ax.
Solution:
Equation of parabola,
y² = 4 ax
Equation of straight line,
lx + my + n = 0
⇒ my = -lx – n

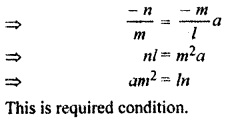
Question 5.
Prove that the length of focal chord of parabola y² = 4ax making an angle a with x-axis will be 4a cosec² a.
Solution:

coordinates of ends P and Q of chord PQ, making an angle α with x-axis and passing through focus S (a, 0) of parabola y² = 4 ax.
From point Q, draw a line parallel to x – axis and draw PR ⊥ from point P to that line.


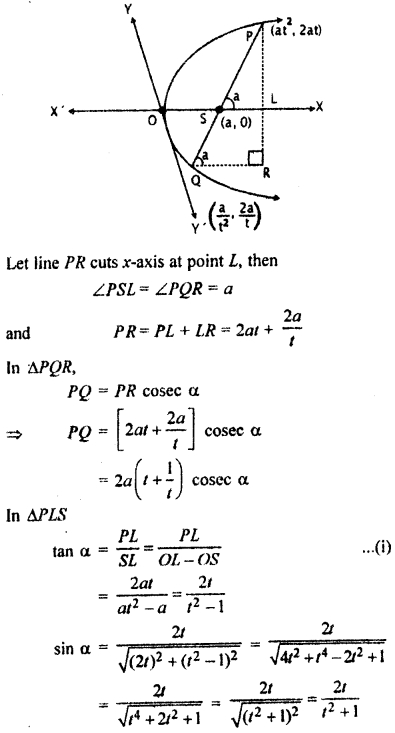
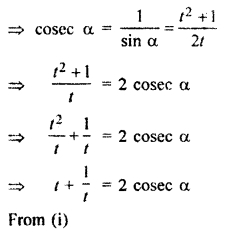
PQ – 2a . 2 cosec α . cosec α
= 4a cosec² α
Thus length of chord PQ = 4a cosec² α.

Question 6.
Find the condition that line x cos α + y sin α – P touches the parabola y² = 4ax
Solution:
Equation of straight line,
x cos α + y sin α = p
⇒ y sin α = – x cos α + p

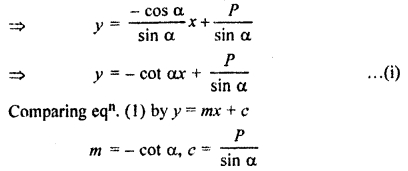
By the condition of tangency of parabola y² = 4ax to straight line y = mx + c

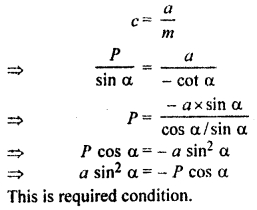
Question 7.
Find the equation of tangents at the following parabolas:
(i) y² = dx, which is parallel to line 2x – 3y = 4
(ii) y² = 8x, which is perpendicular to line 2x – y + 1 = 0
Solution:
(i) Equation of parabola,
y² = 6x
Equation of straight line,
2x – 3y = 4
⇒ 2x – 3y – 4 = 0
Equation of line parallel to this line,
2x – 3y + k = 0
Line (i) will touch parabola y² = 6x if equation

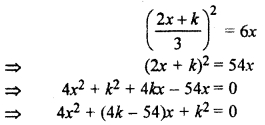
has equal roots, for which condition,
B² = 4AC
⇒ (4k – 54)² = 4 × 4 × k²
⇒ (4k – 54)² – (4k)² = 0
⇒ (4k – 54 – 4k) (4k – 54 + 4k) = 0
⇒ (-54) (8k – 54) = 0

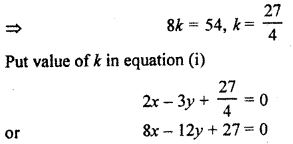
This is required equation.
(ii) Equation of parabola
y² = 8x
Equation of line,
2x – y + 1 = 0
Equation of line perpendicular to this line,
x + 2y – 2k = 0 …(i)
Line (i) will touch the parabola y² = 8x, if

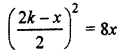
⇒ 4k² + x² – 4kx – 32x = 0
⇒ x² +(-4k – 32)x + 4k² = 0
Its roots will be same, if
B² = 4AC
⇒ (-4k – 32)² = 4 × 1 × 4k²
⇒ (-4k – 32)² – (4k)² = 0
⇒ (- 4k – 32 – 4k)(-4k – 32 + 4k) = 0
⇒ 8k = -32
⇒ k = -4
Putting value of k in equation (i)
x + 2y – 4 = 0
This is required equation.

Question 8.
For which value of k line 2x – 3y-k will touch parabola y² = 6x ?
Solution:
Equation of line,
2x – 3y = k
⇒ 3y = 2x – k

Question 9.
Find the equation of tangents which are drawn from point (4, 10) to parabola y² = 8x.
Solution:
From point (x₁, y₁) two tangents can be drawn at parabola whose combined equation can be find by equation SS’ = T²
Given Point – (4, 0)
Equation of parabola,
⇒ y² = 8x where a = 2
then S = y² – 4ax₁
⇒ S = y² – 8x …(i)
S’ = y1² – 4ax²
⇒ S’ = (10)² – 4 × 2 × 4
⇒ S’ = 100 – 32 = 68 …(ii)
T = yy1 – 2a(x + x₁)
⇒ T = y × 10 – 2 × 2 × (x + 4)
= T = 10y – 4(x + 4)
T² = {10y – 4(x + 4)}²
⇒ T² = 100 y² + 16(x + 4)² – 80(x + 4)y
⇒ T² = 100y² + 16x² + 256 + 128x – 80xy- 320y …(iii)
Put the values from eqn. (i), (ii), (iii) in SS’ – T²
(y² – 8x) (68) = 16x² + 100y² – 80xy + 128x – 320y + 256
⇒ 68y² – 744x – 16x² – 100y²
+ 80xy – 128x+ 320y – 256 = 0
⇒ – 16x² – 32y² + 80xy – 672x + 320y – 256 = 0
⇒ x² + 2y² – 5xy + 42x – 20y + 16 = 0
This is required equation.

Question 10.
Find the equation of normal at the following parabolas:
(i) At point (2, 4) on y² = 8x
(ii) Upper side of latus rectum of
y² + 12x = 0
Solution:
(i) Equation of parabola,
y² = 8x
Point (2, 4), equation of normal at point (x₁, y₁) on parabola y² = 4 ax

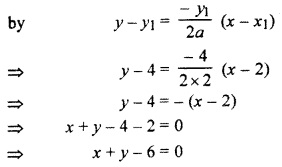
This is required equation.
(ii) y² + 12x = 0
⇒ y² = -12x
⇒ y² = 4(-3)x
Comparing it by y² = 4ax
a = – 3
Equation of latus rectum x = a
⇒ x = – 3
Putting x = – 3 in the equation of parabola

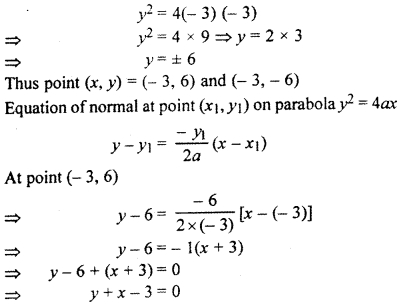
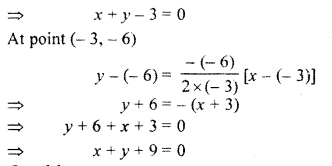
Question 11.
Find the equation of normal at following parabolas :
(i) y² = 4x which is parallel to line y – 2x + 5 = 0
(ii) y² = 4x which is perpendicular to line
x + 3y – 1 = 0
Solution:
(i) Equation of parabola,
y² = 4x
Comparing with y² = 4ax
a = 1
Equation of line y – 2x + 5 = 0
⇒ y = 2x – 5
Comparing with y = mx + c
m = 2, c = – 5
At parabola y² = 4ax parallel to line y = mx + c, eqⁿ. of normal from y = mx – 2am – am³
y = 2x – 2 × 1 × 2 – 1 × (2)³
⇒ y = 2x – 4 – 8
⇒ 7 – 2x + 12 = 0
⇒ 2x – y – 12 =0
This is required equation.
(ii) Equation of parabola,
y² = 4x
Comparing with y² = 4ax.
a = 1

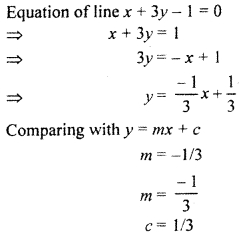
Equation of normal of parabola y² = 4ax, perpendicular to line 7 = mx + c

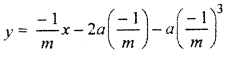
⇒ y = 3x – 2 × 1 × 3 – 1 × (3)³
⇒ y = 3x – 6 – 27
⇒ y = 3x – 33
⇒ 3x – y – 33 = 0
This is required equation.

Question 12.
Prove that line 2x + y – 12a = 0 is normal chord at parabola y² = 4ax and its length is 5\(\sqrt { 5a }\)
Solution:
Equation of line,
2x + y – 12a = 0
⇒ y = – 2x + 12a …(i)
Equation of parabola,
y² = 4ax …(ii)
Put value of y from (i) in (ii),
(-2x + 12a)² = 4ax
⇒ 4x² + 144a² + 2(-2x) (12a) – 4ax = 0
⇒ 4x² + 144a² – 48ax – 4ax = 0
⇒ 4x² – 52ax + 144a² = 0
⇒ x² – 13ax + 36a² = 0
⇒ x² – 9ax – 4ax + 36a² = 0
⇒ x(x – 9a) – 4a(x – 9a) = 0
⇒ (x – 9a) (x – 4a) = 0
x = 4a, 9a
Put these value of x in equation (i),
y² = 4a × 4a ⇒ y = 4a
y² = 4a × 9a ⇒ y = 6a
Thus coordinates of ends of latus rectum are (4a, 4a) and (9a, – 6a)
∵ Coordinates will lie in 1st and 4th quadrant will be (+, +) and (+, -).
Thus length of latus rectum

RBSE Solutions for Class 11 Maths