Rajasthan Board RBSE Class 11 Maths Chapter 2 Relations and Functions Ex 2.1
Question 1.
If A = {1, 2, 3}, B = {4, 5, 6}, then which of the following is relation from A to B? Justify your answer also.
(i) {(1, 4), (3, 5), (3, 6)
(ii) {(1, 6), (2, 6), (3, 6)}
(iii) {(1, 5), (3, 4), (5, 1), (3, 6)}
(iv) {(2, 4), (2, 6), (3, 6), (4, 2)}
(v) A × B
Solution:
Here, A = {1, 2, 3}, B = {4, 5, 6}
Then A × B = {(1, 4), (1, 5), (1,6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)}
(i) Let R1 = {(1, 4), (3, 5), (3, 6)}
(1, 4) ∈ A × B
(3, 5) ∈ A × B
(3, 6) ∈ A × B
R1 ⊆ A × B
Hence, R1 is a relation from A to B.
(ii) Let R2 = {(1, 6), (2, 6), (3, 6)}
(1, 6) ∈ A × B
(2, 6) ∈ A × B
(3, 6) ∈ A × B
R2 ⊆ A × B
R2 = {(1, 6), (2, 6), (3, 6)}
Hene, R2 is a relation from A to B.
(iii) R3 = {(1, 5), (3, 4), (5, 1), (3, 6)}
(1, 5) ∈ A × B
(3, 4) ∈ A × B
(5, 1) ∉ A × B
R3 ⊄ A × B
Hence, R3 is not a relation from A to B.
(iv) Let R4 = {(2, 4), (2, 6), (3, 6), (4, 2)}
(2, 4) ∈ A × B but (4, 2) ∉ A × B
R4 ⊄ A × B
Hence, R4 is not a relation from A to B.
(v) A × B ⊆ A × B
Hence, it is a relation.
Question 2.
Express the following relations in the rules form defined in N:
(i) {(1, 3), (2, 5), (3, 7), (4, 9), …}
(ii) {(2, 3), (4, 2), (6, 1)}
(iii) {(2, 1), (3, 2), (4, 3), (5, 4), …}
Solution:
(i) N = (1, 2, 3, …}
The relation from N to N is given by: {(1, 3), (2, 5), (3, 7), (4, 9), …}
when, x = 1 then y = 3
x = 2 then y = 5
x = 3 then y = 7
x = 4 then y = 9
3, 5, 7, 9, … is an A.P.
Hence, its nth term = a + (n – 1 ).d, where a is first term and d, is a common difference.
Tn = 3 + (n – 1) × 2 = 3 + 2n – 2 = 2n + 1
Here, we get the requied rule by putting n = x and Tn = y
{(x, y) | x, y ∈ N and y = 2x + 1}.
(ii) Relation in N is expressed as :
{(2, 3), (4, 2), (6, 1)} = {(6, 1), (4, 2), (2, 3)}
Here, 6, 4, 2 are in an A.P.
Its general term Tn = 6 + (n – 1) × (-2)
Tn = 6 – 2n + 2
Tn = 8 – 2n
Here, we get the required rule by putting x = y and Tn = x
{(x, y) | x, y ∈ N, x = 8 – 2y or x + 2y = 8} and y < 4
(iii) Relation in N is expressed as:
{(2, 1), (3, 2), (4, 3), (5, 4), …}
Here, 2, 3, 4, 5, … are in an A.P.
So, nth term Tn = 2 + (n – 1) × 1 = 2 + n – 1 = n + 1
Here, by putting n = x and Tn = y
Required rule = {(x, y) | x, y ∈ N, x = y + 1 or y = x – 1}
Question 3.
A relation R from set A = {2, 3, 4, 5} to set B = {3, 6, 7, 10} is defined in such a way that xRy ⇔ x is a prime number related to y. Write relation R in the set form or order pairs and also find domain and range of if.
Solution:
Given, A = {2, 3, 4, 5}, B = (3, 6, 7, 10}
Relation R from A to B is defined as:
xRy ⇔ x, y is a prime number related by ∀ x, y ∈ R
(Numbers a and b are called co-prime if there is no common factor except 1 for example 3 is co-prime related to 10)
x = 2 ∈ A then 2 is a prime number related to 3 and 7.
Then (2, 3) ∈ R and (2, 7) ∈ R
when x = 3 ∈ A
then 3 is a prime number related to 7 and 10.
Then (3, 7) ∈ R and (3, 10) ∈ R
when x = 4 ∈ A
then 4 is a prime number related to 3 to 7.
then (4, 3) ∈ R and (4, 7) ∈ R
when x = 5 ∈ A then 5 is a prime number related to 3, 6 and 7.
then (5, 3) ∈ R, (5, 6) ∈ R and (5, 7) ∈ R
Hence R = {(2, 3), (2, 7), (3, 7), (3, 10), (4, 3), (4, 7), (5, 3), (5, 6), (5, 7)}
Domain of R = {2, 3, 4, 5}
and range of R = {3, 6, 7, 10}.
Question 4.
If in a set of integers Z, a relation R is defined in such a way that xRy ⇔ x2 + y2 = 25, then write R and R-1 in the form of a set of order pairs and also write their domain.
Solution:
Given set = 2
Z = {Set of integers} = {0, ± 1, ± 2, ± 3, …}
Relation in Z i.e., a relation R from Z to Z is defined as
xRy ⇔ x2 + y2 = 25 ∀ x, y ∈ Z
when x = 0 then y = ± 5 because from 02 + y2 = 25
⇒ (0, 5) ∈ R and (0, -5) ∈ R
when x = ±3
(±3)2 + y2 = 25
⇒ y2 = 25 – 9 = 16
⇒ y = ±4
then (3, 4) ∈ R and (-3, 4) ∈ R
(-3, 4) ∈ R (-3, -4) ∈ R
when x = ± 4 then y = ± 3
from (±4)2 + y2 = 25
⇒ y2 = 25 – 16 = 9
⇒ y = ± 3
⇒ (4, 3) ∈ R, (4, -3) ∈ R,
(-4, 3) ∈ R, (-4, -3) ∈ R
when x = ± 5 then y = 0
(±5)2 + y2 = 25
⇒ y2 = o
⇒ y = 0
⇒ (5, 0) ∈ R and (-5, 0) ∈ R
Hence,
R={(0, 5), (0, -5), (3, 4), (-3, 4), (3, -4), (-3, -4), (4, 3), (4, -3), (-4, 3), (-4, -3), (5, 0), (-5, 0)}
and R-1 = {(5, 0), (-5, 0), (4, 3), (4, -3), (-4, 3), (-4, -3), (3, 4), (-3, 4), (3, -4), (-3, -4), (0, 5), (0, -5)}
Domain of R = {0, 3, -3, 4, -4, 5, -5}
and domain of R-1 = {5, -5, 4, -4, 3, -3, 0}.
Question 5.
If a relation Φ from set C of complex numbers to a set R of real numbers is so defined that
x Φ y ⇔ |x|= y.
(i) (1 + i)Φ3
(ii)3Φ(-3)
(iii) (2 + 3i)Φ13
(iv) (1 + i)Φ1
Solution:
Given set
C = {a + ib : a ∈ R, b ∈ R, i = √-1} = Set of complex number
R = Set of real number
Relation Φ from C to R is defined as:
x Φ y ⇔ |x|= y ∀ x ∈ c, y ∈ R
(i) (1 + i)Φ3
|1 + i|= √(12 + 12) = √2 ≠ 3
Hence, (1 + i)Φ3 is false.
(ii) 3Φ(-3)
|3|= 3 ≠ -3
Relation Φ is false.
(iii) (2 + 3i)Φ13
|2 + 3i|= √(22 + 32) = √(4 + 9) = √13 ≠ 13
Relation is false.
(iv) (1 + i)Φ1
|1 + i| = √(12 + 12) = √2 ≠ 1
Hence, relation is false.
Question 6.
If a relation R from set A = {1, 2, 3, 4, 5} to set R = {1, 4, 5} is defined such that x < y, then write R in the form of set of order pairs. Also find R-1
Solution:
Given that, a relation R from A to B is defined as:
xRy ⇔ x < y ∀ x ∈ A, y ∈ B
1 ∈ A
1 < 4, 1 < 5
So, (1, 4) ∈ R and (1, 5) ∈ R
Again 2 ∈ A and 2 < 4, 2 < 5
So, (2, 4) ∈ R, (2, 5) ∈ R
Again 3 ∈ A and 3 < 4, 3 < 5
So, (3, 4) ∈ R, (3, 5) ∈ R
Again 4 ∈ A and 4 < 5
So, (4, 5) ∈ R
R = {(1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}
and R-1 = {(4, 1), (5, 1), (4, 2), (5, 2), (4, 3), (5, 3), (5, 4)}
Question 7.
Express the following relations in the form of sets or orders pairs:
(i) R1 is relation from set A = {1, 2, 3, 4, 5, 6} to set B = (1, 2, 3} such that “x = 2y”.
(ii) R2 is a relation set A = {8, 9, 10, 11} to set B = {5, 6, 7, 8} such that “y = x – 2”.
(iii) R3 is a relation in set A = {0, 1, 2,…, 10} defined by 2x + 3y = 12.
(iv) R4 is a relation from set A = {5, 6, 7, 8} to set B = {10, 12, 15, 16, 18} is defined such that “x is divisor of y”
Solution:
(i) Given relation R1 is defined as “x = 2y” and A = {1, 2, 3, 4, 5, 6} and in B = {1, 2, 3}
x = 2y
y = \(\frac { x }{ 2 }\)
when x = 2 then y = 1. So, (2, 1) ∈ R1
when x = 4 then y = 2. So, (4, 2) ∈ R1
and x = 6 then y = 3. So, (6, 3) ∈ R1
R1 = {(2, 1), (4, 2), (6, 3)}
(ii) Given relation R2 is defined as “y = x – 2” and A = {8, 9, 10, 11} and B= {5,6, 7,8}
So, from y = x – 2
when x = 8 then y = 8 – 2 = 6 So, (8, 6) ∈ R2
when x = 9 then y = 9 – 2 = 7 So, (9, 7) ∈ R2
when x = 10 then y = 10 – 2 = 8 So, (10, 8) ∈ R2
and when x = 11 then y = 11 – 2 = 9 So, (11, 9) ∈ R2
R2 = {(8, 6), (9, 7), (10, 8)}
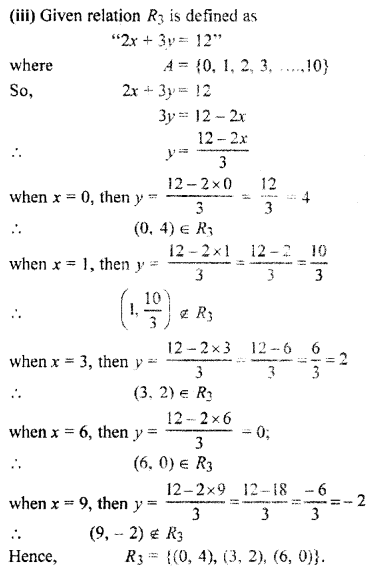
(iv) Given relation R4 is defined as “x, y”
A = {5, 6, 7, 8}
and B = {10, 12, 15, 16, 18}
So, xR4y ⇔ x is divisor of y
x ∈ A, y ∈ B
when x = 5 then 5 is a divisor of 10 and 15
So, (5, 10), (5, 15) ∈ R4
when x = 6 then 6 is a divisor of 12 ahd 18
So, (6, 12), (6, 18) ∈ R4
when x = 8 then 8 is a divisor of 16
So, (8, 16) ∈ R4
R4 = (5, 10), (5, 15), (6, 12), (6, 18), (8, 16)}
Question 8.
Find the inverse of each of the following relation:
(i) R = {(2, 3), (2, 4), (3, 3), (3, 2), (4, 2)}
(ii) R = {(x, y) | x, y ∈ N; x < y}
(iii) R is defined by 2x + 3y = 12 in set A = (0, 1, 2, …10}.
Solution:
(i) Given that
R = {(2, 3) (2, 4), (3, 3), (3, 2), (4, 2)}
R-1 = {(3, 2), (4, 2), (3, 3), (2, 3), (2, 4)}
(ii) Given that
R = {(x, y) | x, y ∈ N; x < y}
R-1 = {(y, x) | x, y ∈ N; x > y}
(iii) Relation in set A is defined by
2x + 3y = 12
R = {(0, 4), (3, 2), (6, 0)}
R-1 = {(4, 0), (2, 3), (0, 6)}.