Rajasthan Board RBSE Class 11 Maths Chapter 2 Relations and Functions Ex 2.2
Question 1.
Examine the reflexivity, symmetricity, and transitivity of the following relations:
(i) mR1n ⇔ m and n both are odd, ∀ m, n ∈ N
(ii) In the power set P(A) of set AR2B ⇔ A ⊆ B, ∀ A, B ∈ P(A)
(iii) In set B of straight lines situated in three dimensions space, L1R3L2 ⇔ L1 and L2 are coplanar ∀ L1, L2 ∈ S
(iv) aR4b ⇒ b is divisible by a, ∀ a, b ∈ N.
Solution:
(i) Given, set N = {1, 2, 3, 4, …}
A relation R1 in N is defined as
mR1n ⇔ m and n both are odd ∀ m, n ∈ N
Reflexivity: Let m ∈ N
m ∈ N ⇒ m : even or odd number
⇒ (m, m) ∈ R1 If m is odd
But (m, m) ∉ R1 If m is even
So, (m, m) ∉ R1
R1 is not reflexivity.
Symmetricity: Let m, n ∈ N, mR1 is true,
So, mR1n ⇒ m and n are both odd.
⇒ n and m are both odd
⇒ nR1m
R1 is a symmetric relation.
Transitivity: Let m, n, r ∈ N
mR1n and nR1r is true, so,
mR1n and nR1r ⇒ m and n are both odd and n, r are both odd.
⇒ m, n and r are odd.
⇒ mR1r
R1 is transitive relation.
(ii) Given set is
AR2B ⇔ A ⊆ B ∀ A, B ∈ P(A)
Reflexivity: Let A ∈ P(A)
A ∈ P(A) ⇒ A ⊆ A (∵ every set is a subset of itself)
⇒ AR2A
Hence, R2 reflexive relation.
Symmetricity: Let A, B ∈ P(A), AR2B are true, so,
AR2B ⇒ A ⊆ B
⇒ B ⊄ A (until A = B)
⇒ B ⊄ A
R2 is not a symmetric relation.
Transitivity: A, B, C ∈ P(A),
AR2B and BR2C are true. So,
AR2B and BR2C
⇒ A ⊆ B and B ⊆ C
⇒ A ⊆ C(A ⊆ B ⊆ C)
⇒ AR2C
R2 is transitive relation.
(iii) Given set is
S = {Set of straight lines situated in three dimensional space}
A relation R3 in S is defined as
L1R3L2 ⇒ L1 and L2 are co-planar lines ∀ L1, L2 ∈ S
Reflexivity: Let L ∈ S
L ∈ S ⇒ L and L are coplanar
⇒ (L, L) ∈ R3 ∀ L ∈ S
R3 is a reflexive relation.
Symmetricity: Let L1, L2 ∈ S
In this way (L1, L2) ∈ R3
(L1, L2) ∈ R3
⇒ L1 and L2 are coplanar
⇒ L2 and L1 are coplanar
⇒ (L2, L1) ∈ R3
So, (L1, L2) ∈ R3
⇒ (L2, L1) ∈ R3 ∀ L1, L2 ∈ S
R3 is a symmetric relation.
Transitivity: Let L1, L2, L2 ∈ S is given as
(L1, L2) ∈ R3 and (L2, L3) ∈ R3
(L1, L2) ∈ R3 ⇒ L1 and L2 are coplanar ……(1)
(L2, L3) ∈ R3 ⇒ L2 and L3 are coplanar …(2)
So, from (1) and (2) we can not say that L1 and L3 are also coplanar.
From figure L1 and L2 are situated in a plane (1),
L2 and L3 are situated in a plane (2)
but L1 and L3 are not coplanar.
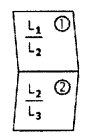
So, (L1, L3) ∉ R3
R3 is not a transitive relation.
(iv) Given set is N = {1,2, 3, 4, …}
Relation R4 in N is defined as
aR4b ⇔ b is divided by a ∀ a, b ∈ N
⇔ \(\frac { 1 }{ 2 }\) = k ∈ I
where I is the set of integers ∀ a, b ∈ N
⇔ ∀ a is divided by b
∀ a, b ∈ N
Reflexivity: Let a ∈ N
a ∈ N ⇒ a is divided by a
⇒ (a, a) ∈ R4 ∀ a ∈ N
R4 is a reflexive relation.
Symmetricity: Let a, b ∈ N is in this way (a, b) ∈ R4
(a, b) ∈ R4 ⇔ b is divided by a
⇔ a cannot be divided by b until a = b
⇔ (b, a) ∉ R4
(a, b) ∈ R4 ⇔ (b, a) ∉ R4
So, R4 is not a symmetric relation.
Transitivity: Let a, b, c ∈ N
In this way
(a, b) ∈ R4 and (b, c) ∈ R4
(a, b) ∈ R4 ⇒ b is divided by a
⇒ \(\frac { b }{ a }\) = k (Let) where k ∈ I …(1)
(b, c) ∈ R4 ⇒ c is divided by b
⇒ \(\frac { c }{ b }\) = m (Let) where m ∈ I …(2)
Putting the value of b from equation (1) in equation (2) we have
m ∈ I, k ∈ I
mk ∈ I
\(\frac { c }{ ak }\) = m ⇒ \(\frac { c }{ a }\) = mk ∈ I
⇒ (a, c) ∈ R4
(a, b) ∈ R4, (b, c) ∈ R4
⇒ (a, c) ∈ R4 ∀ a, b, c ∈ N
Hence, R4 is a transitive relation.
Question 2.
Any relation P is defined in set R0 of non zero real numbers by following ways:
(i) xPy ⇔ x2 + y2 = 1
(ii) xPy ⇔ xy = 1
(iii) xPy ⇔ (x + y) is a rational number
(iv) xPy ⇔ x/y is a rational number
Test the reflexivity, symmetricity and transitivity of these relations.
Solution:
(i) Given set
R0 = Set of non-zero real number
Relation P in R0 is defined as
xPy = x2 + y2 = 1 ∀ x, y ∈ R0
Reflexivity: P is not reflexivie because when 2 ∈ R0
Then (2)2 + (2)2 ≠ 1 so, (2, 2) ∉ R0
Similarly a2 + a2 ≠ 1 so, (a, a) ∉ R0
Hence, P is not reflexive.
Symmetricity: Let a, b ∈ R0
In this way (a, b) ∈ P
(a, b) ∈ P
⇒ a2 + b2 = 1
⇒ b2 + a2 = 1
⇒ (b, a) ∈ P
So, (a, b) ∈ P
⇒ (b, a) ∈ P ∀ a, b ∈ R0
P is symmetric relation.
Transitivity: P is not transitive relation because
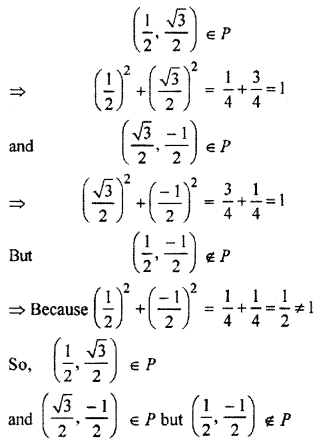
P is not transitive relation.
(ii) Given set R0 = {Set of real numbers}
Relation P in R0 is defined as
xPy ⇔ xy = 1 ∀ x, y ∈ P
Reflexivity: Let 2 ∈ R0
But 2 × 2 = 4 ≠ 1
⇒ (2, 2) ∉ P
Hence, P is not reflexive
Symmetricity: In this way (a, b) ∈ R0
In this way (a, b) ∈ P
(a, b) ∈ P
⇒ ab = 1
⇒ ba = 1 [∵ Multiplication of real number is commutative]
⇒ b . a ∈ P
⇒ (a, b) ∈ P
⇒ (b, a) ∈ P ∀ a, b ∈ R0
P is a symmetric relation.
Transitivity: Let a, b, c ∈ R0 is in this way
a, b ∈ P and b, c ∈ P
(a, b) ∈ P ⇒ a.b = 1 ……(1)
(b, c) ∈ P ⇒ b.c = 1 …..(2)
From equation (1) and (2),
\(\frac { ab }{ bc }\) = \(\frac { 1 }{ 1 }\)
⇒ \(\frac { a }{ c }\) = 1
⇒ (a, c) ≠P ……..(3)
So, (a, b) ∈ P, (b, c) ∈ P but (a, c) ∉ P
Hence, P is not transitive relation.
(iii) Given set R0 = Set of real number
Relaton P in R0 is defined as
xPy ⇔ x + y is a rational number ∀ x, y ∈ R0
Reflexivity : Let x ∈ R0
x ∈ R0 ⇒ x + x is need not to be rational
For example √3 ∈ R0 ⇒ √3 + √3 = 2√3
is an irrational number
So, (x, x) ∉ P
P is not reflexive relation.
Symmetricity: Let a, b ∈ R0 then (a, b) ∈ P
(a, b) ∈ P
⇒ a + b is a rational number
⇒ (b + a) is also a rational number
⇒ (b, a) ∈ P
So, (a, b) ∈P
⇒ (b, a) ∈ P ∀ a, b ∈ R0
P is a symmetric relation.
Transitivity: Let a, b, c ∈ R0 are in this way
(a, b) ∈ P ⇒ a + b is a rational number
(b, c) ∈ P ⇒ b + c is a rational number
⇒ a + c is not necessary a rational number
For example: 2 + √3, -√3 + 6, √3 + √7 ∈ Ro and (2 + √3, -√3 + 6) ∈ P because
2 + √3 – √3 + 6 = 8 is a rational number
(-√3 + 6, √3 + 7) ∈ P because
-√3 + 6 + √3 + 7 = 13 is a rational number
But (2 + √3, √3 + 7) ∈ P because
2 + √3 + √3 + 7 = 2√3 + 9 is an irrational number
Hence, P is not a transitive relation.
(iv) Given: Set : R0 = Set of real numbers
Relation P in R0 is defined as a rational number
xPy = \(\frac { x }{ y }\) is a rational number ∀ x, y ∈ R0
Reflexivity: Let a ∈ R0
a ∈ R0 ⇒ \(\frac { a }{ a }\) = 1 is a rational number
⇒ (a, a) ∈ P
P is a reflexive number.
Symmetricity: Let a, b ∈ R0 is in this way (a, b) ∈ P
(a, b) ∈ P
⇒ \(\frac { a }{ b }\) is a rational number
⇒ \(\frac { b }{ a }\) is a rational number
(From infination of set of rational numbers Q)
⇒ (b, a) ∈ P
(a, b) ∈ P
⇒ (b, a) ∈ P ∀ a, b ∈ R0
P is a symmetric relation
Transitivity: Let a, b, c ∈ R0 is in this way
(a, b) ∈ P and (b, c) ∈ P
(a, b) ∈ P ⇒ \(\frac { a }{ b }\) is a rational number
(b, c) ∈ P ⇒ \(\frac { b }{ c }\) is a rational number
⇒ (\(\frac { a }{ b }\))(\(\frac { b }{ c }\))is also a rational number.
[∵ Multiplication of rational number is also a rational number]
⇒ \(\frac { a }{ c }\) is a rational number
⇒ (a, c) ∈ P
(a, b) ∈ P, (b, c) ∈ P
⇒ (a, c) ∈ P ∀ a, b, c ∈ R0
P is a transitive relation.
Question 3.
A relation R1 is defined in set R if of real numbers in the following way:
(a, b) ∈ R1 ⇔ 1 + ab > 0, ∀ a, b ∈ R
Prove that R1 is reflexive and symmetric but not transitive.
Solution:
Given: Set R = set of real numbers.
Relation R1 in R is defined as
(a, b) ∈ R1 ⇒ 1 + ab > 0 ∀ a, b ∈ R
(i) Reflexivity: Let a ∈ R
a ∈ R ⇒ 1 + a.a > 0
⇒ a.a ∈ R1 ∀ a ∈ R
R1 is a reflexive relation.
(ii) Symmetricity: Let a, b ∈ R in this way
(a, b) ∈ R1
(a, b) ∈ R1
⇒ 1 + ab > 0
⇒ 1 + b.a > 0 [ab = ba]
⇒ (b, a) ∈ R1
So, (a, b) ∈ R1
⇒ (b, a) ∈ R1 ∀ a, b ∈ R
R1 is a symmetric relation.
(iii) Transitivity: Let a, b, c ∈ R is in this way
(a, b) ∈ R1 and (b, c) ∈ R1
(a, b) ∈ R1 ⇒ 1 + ab > 0
(b, c) ∈ R1 ⇒ 1 + bc > 0
But 1 + ac > 0 is not necessary.
For example: 1, \(\frac { 1 }{ 2 }\), -1 ∈ R
and (1, \(\frac { 1 }{ 2 }\)) ∈ R1 because
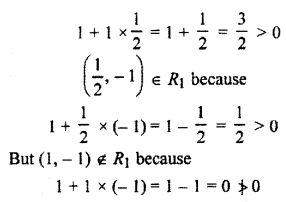
R1 is not a transitive relation.
Hence Proved.
Question 4.
N is a set of natural numbers. If a relation R is defined in set N × N such that (a, b) R(c, d) ⇔ ad = bc ∀ (a, b), (c, d) ∈ N × N, then prove that R is an equivalence relation.
Solution:
Given:
Set N = {1, 2, 3, 4, …} = Set of natural numbers
A relation R in N × N is defined as
(a, b) R(c, d) ⇔ ad = bc where a, b,c, d ∈ N ∀ (a, b), (c, d) ∈ N × N
Here, to prove R is a equivalence relation, we have to show that R is reflexive, symmetric and transitive.
(i) Reflexivity: Let
(a, b) ∈ N × N
{a, b) ∈ N × N
⇒ a.b = ba (Commutative law of multiplication)
⇒ (a, b) R(a, b) ∀ (a, b) ∈ N × N
R is reflexive relation.
(ii) Symmetricity: Let (a, b) (c, d) ∈ N × N is in this way (a, b) R(c, d)
(a, b) R(c, d)
⇒ ad = bc
⇒ bc = ad
⇒ c.b = d.a
⇒ (c, d) R(a, b)
So, (a, b) R(c, d) ⇒ (c, d) R(a, b) ∀ (a, b)(c, d) ∈ N × N
R is a symmetric relation.
(iii) Transitivity: Let
(a, b), (c, d), (e, f) ∈ N × N
is in this way
(a, b) R(c, d) and (c, d) R(e, f)
(a, b) R(c, d) ⇒ ad = bc
(c, d) R(e, f) ⇒ cf = de
(a, b)R (c, d) and (c, d)R (e, f)
⇒ (ad) (cf) = (bc)(de) (on multiplication)
⇒ af = be
⇒ (a.b) R(e, f)
So, (a, b) and R(c, d) and (c, f) R(e, f)
⇒ (a, b) R(e, f) ∀ (a, b), (c, d), (e, f) ∈ N × N
R is a transitive relation.
Hence, according to (i), (ii) and (iii), the given relation is an equivalence relation.
Hence Proved.
Question 5.
A relation R is defined in a set Q0 set of non zero rational numbers such that aRb ⇔ a = 1/b, ∀ a, b ∈ Q0. Is R is equivalence relations.
Solution:
Given: Set Q0 = Set of non zero rational numbers
A relation in Q0 is defined as
aRb ⇔ a = 1/b ∀ a, b ∈ Q0
If R is reflexive, symmetric and transitive than R is an equivalence relation.
(i) Reflexivity: Let a ∈ Q0
a ∈ Q0 ⇒ a ≠ \(\frac { 1 }{ a }\) (a ≠ 1)
⇒ (a, a) ∉ R ∀ a ∉ Q0
So, R is not a reflexive relation
R is also not equivalenced relation.
Question 6.
Let {(a, b) | a, b ∈ R} where I is set of integers. Relations R1 on x is defined in the following way
(a, b) R1(c, d) ⇒ b – d = a – c
Prove that R1 is an equivalence relation.
Solution:
Given : Set X = {(a, b) : a, b ∈ I}
where I is the set of integers.
A relation R in X is defined as:
(a, b) R(c, d) ⇔ b – d = a – c ∀ (a, b) (c, d) ∈ X
To prove that R is equivalence relation, we have to prove that R is reflexive, symmetric and transitive.
(i) Reflexivity: Let (a, b) ∈ X
(a, b) ∈ X ⇒ (a, b) ∈ I
⇒ b – b = a – a = 0
⇒ (a, b) R(a, b) ∀ (a, b) ∈ X
R is a reflexive relation.
(ii) Symmetricity: Let (a, b), (c, d) ∈ X is in this way
(a, b) R(c, d)
(a, b) R(c, d)
⇒ b – d = a – c
⇒ -(d – b) = -(c – a)
⇒ d – b = c – a
⇒ (c.d) R(a.b)
(a, b) R(c, d) ⇒ (cd) R(ab) ∀ (a, b), (c, d) ∈ X
R is a symmetric relations.
(iii) Transitivity: Let (a, b), (c, d), (e, f) ∈ X is in this way (a, b) R(c, d) and (c, d) R(e, f)
(a, b) R(c, d) ⇒ b – d = a – c …(1)
(c, d) R(e, f) ⇒ d – f = c – e …(2)
Adding equation (i) and (2), we have
b – d + d – f = a – c + c – e
⇒ b – f = a – e
⇒ (a, b) R(e, f)
So, (a, b) R(c, d) and (c, d) R(e, f)
⇒ (a, b) R(e, f) ∀ (a, b), (c, d), (e, f) ∈ X
R is a transitive relation.
Hence, according to (i), (ii) and (iii), the given relation is equivalence relation.
Hence Proved.
Question 7.
A relation R is defined in a set T of triangles situated in a plane such that xRy ⇔ x is similar to y. Prove that R is an equivalence relation.
Solution:
Given : Set T = {Set of similar triangles}
A relation R in T is defined as:
xRy ⇔ x is similarly to y ∀ x, y ∈ T
To prove R is an equivalence relation, we have to prove that R is reflexive, symmetric and transitive.
(i) Symmetricity: Let x ∈ T
x ∈ f ⇒ x is similar to x.
⇒ (x, x) ∈ R ∀ x ∈ T
R is a reflexive relation.
(ii) Symmetricity: Let x, y ∈ T is in this way
(x, y) ∈ R
(x, y) ∈ R ⇒ x is similar to y
⇒ y is similar to x
⇒ (y, x) ∈ R
So, (x, y) ∈ R ⇒ (y, x) ∈ R ∀ x, y ∈ T
R is a symmetric relation.
(iii) Transitivity: Let x, y, z ∈ T is in this way
(x, y) ∈ R, (y, z) ∈ R
(x, y) ∈ R ⇒ x is similar to y.
(y, z) ∈ R ⇒ y is similar to z.
set x is similar to z.
So, (x, y) ∈ R, (y, z) ∈ R ⇒ (x, z) ∈ R ∀ x, y, z ∈ T
R is a transitive relation.
Hence, according to (i), (ii) and (iii), the given relation is an equivalence relation.
Hence Proved.
Question 8.
Let a relation R is defined in a set A = {1, 2, 3} as : R = {(1, 1), (1, 2), (2, 1) (2, 2), (3, 3), (1, 3), (3, 1), (2, 3), (3, 2)} Examine the reflexivity,
symmetricity and transitivity of R.
Solution:
Given set A = {1, 2, 3}
Reiation R In A is defined as:
R = {(1, 1), (1, 2), (2, 1), (2, 2), (3, 3), (1, 3), (3, 1), (2, 3), (3, 2)}
(i) Reflexivity: Here (1, 1), (2, 2), (3, 3) ∈ R
So, ∀ a ∈ A ⇒ (a, a) ∈ R
R is reflexive.
(ii) Symmetricity: Here, R is symmetric, because
(1, 2) ∈ R ⇔ (2, 1) ∈ R
(1, 3) ∈ R ⇔ (3, 1) ∈ R
(3, 2) ∈ R ⇔ (2, 3) ∈ R
So, (a, b) ∈ R ⇔ (b, a) ∈ R ∀ a, b ∈ A
So, R is a transitive relation.
(iii) Transitivity: (1, 2) ∈ R, (2, 1) ∈ R
⇒ (1, 1) ∈ R
(2, 3) ∈ R, (3, 2) ∈ R
⇒ (2, 2) ∈ R
Hence, by definition of Transitivity.
(a, b) ∈ R, (b, c) ∈ R
⇒ (a, c) ∈ R ∀ a, b, c ∈ A
So, R is a transitive relation.
Question 9.
A relation R in a set C0 of non zero complex numbers is defined as:
![]()
Prove that R is an equivalence relation.
Solution:
Given: Set C0 = set of the non-zero complex number and a relation R in C0 is defined as:



Hence from (i), (ii) and (iii), the given relation is an equivalence relation.
Hence Proved.
Question 10.
If R is a relation in set X of subsets defined as “A is disjoint to B” then examine the reflexivity, symmetricity and transitivity of R.
Solution:
Set X = set of subsets A relation R in X is defined as
ARB ⇔ A is disjoint to B ∀ A, B ∈ X
⇔ A ∩ B = Φ ∀ A, B ∈ X (where Φ is a null set)
(i) Reflexivity: Let A ∈ X
A ∈ X ⇒ A ∩ A = A
⇒ A ∩ A ≠ Φ (untill A becomes Φ)
⇒ A is not disjoint to A
⇒ (A, A) ∉ R ∀ A ∈ X
R is not reflexive relation.
(ii) Symmetricity: Let A, B ∈ X in this way
(A, B) ∈ R
(A, B) ∈ R
⇒ A is disjoint to B thus A ∩ B = Φ
⇒ B ∩ A thus, B is disjoint to A (By commutative)
⇒ (B, A) ∈ R
So, (A, B) ∈ R ⇒ (B, A) ∈ R ∀ A, B ∈ X
R is a symmetric relation.
(iii) Transitivity: Let A, B, C ∈ X is in this way
(A, B) ∈ R and (B, C) ∈ R
A, B ∈ R ⇒ A ∩ B = Φ
B, C ∈ R ⇒ B ∩ C = Φ
Then A ∩ C = Φ is not necessary.
For example:
A = {1, 2, 3}, B = {4, 5, 6}, C = {1, 2, 7}
Here A, B ∈ R because A ∩ B = Φ
B, C ∈R because B ∩ C ⇒ Φ
But (A, C) ∉ R because A ∩ C = {1, 2} ≠ Φ
R is not transitive relation.
From (i), (ii) and (iii) given relation R is symmetric but relative R is not reflexive and transitive.
Hence Proved.
Question 11.
A relation R is defined in a set N of natural numbers such that aRb if a is a divisor of b, Prove that R is a partially ordered relation but not a total ordered relation.
Solution:
Given set N = {1, 2, 3, 4,…} = Set of natural numbers
Where a relation is define as
aRb ⇔ a is divisor of b ∀ a, b ∈ N
There R is a partial ordered relation if it is reflexive, anti symmetric and transitive.
(i) Reflexivity: Let a ∈ N
a ∈ N ⇒ a is divisor of a
⇒ (a, a) ∈ R ∀ a ∈ N
R is reflexive relation.
(ii) Anti Symmetricity: Let a, b ∈ N is in this way (a, b) ∈ R
(a, b) ∈ R ⇔ a is divisor of b.
⇔ b is disivor of a.
if a = b ∀ a, b ∈ N ⇔ (b, a) ∈ R; a = b, ∀ a, b ∈ N
(a, b) ∈ R ⇔ (b, a) ∈ R ⇒ a = b ∀ a, b ∈ N
So, R is anti-symmetric relation.
(iii) Transitivity: Let a, b, c ∈ N is in this way
(a, b) ∈ R and (b, c) ∈ R
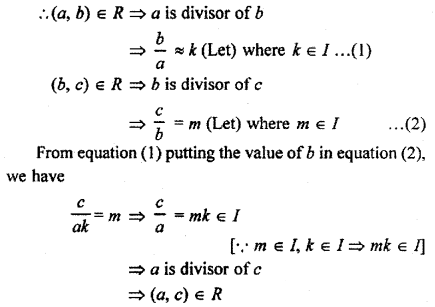
So, (a, b) ∈ R, (b, c) ∈ R ⇒ (a, c) ∈ R ∀ a, b, c ∈ N
So, R is a transitive relation.
Hence, from (i), (ii) and (iii) the given relation is a partially ordered relation.
Hence Proved.
Question 12.
Whether following subsets of N are total ordered set for relaton “x divides y or not” :
(i) {2, 4, 6, 8,……}
(ii) {0, 2, 4, 6,……..}
(iii) (3, 9, 5, 15,…}
(iv) (5, 15, 30}
(v) {1, 2, 3, 4}
(vi) {a, b, ab} ∀ a, b ∈ R.
Solution:
(i) Let subset A = {2, 4, 6, 8, …} ∈ N
A relation given in N
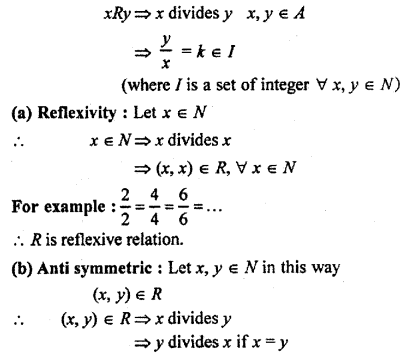


Hence, the second rule is not followed then the given relation is not a total ordered relation. For this it is clear that to prove a relation is a total ordered relative must be reflexive, symmetric and transitive and also every a, b ∈ A, (a, b) ∈ R or (b, a) ∈ R or a = b is true.
Hence, the given relation and their results are:
| Relation | Conclusion |
| (i) (2, 4, 6, 8,…} | No |
| (ii) {0, 2, 4, 6,…} | No |
| (iii) {3, 9, 5, 15,…} | No |
| (iv) {5, 15, 30} | Yes |
| (v) {1, 2, 3, 4} | No |
| (vi) {a, b, ab} ∀ a, b ∈ R | No |