RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3

by

Rajasthan Board RBSE Class 11 Maths Chapter 2 Relations and Functions Ex 2.3

Question 1.
Examine which of the following is/are functions:
(i) {(1, 2), (2, 3), (3, 4), (2, 1)}
(ii) {(a, 0), (b, 0), (c, 1), (d, 1)}
(iii) {(1, a), (2, b), (1, b), (2, a)}
(iv) {(a, a), (b, b), (c, c)}
(v) {(a, b)}
(vi) {(4, 1), (4, 2), (4, 3), (4, 4)}
(vii) {(1, 4), (2, 4), (3, 4), (4, 4)}
(viii) {(x, y) | x, y ∈ R ∧ y2 = x}
(ix) {(x, y) | x, y ∈ R ∧ x2 = y}
(x) {(x, y) | x, y ∈ R ∧ x = y3}
(xi) {(x, y) | x, y ∈ R ∧ y = x3}
Solution:
(i) {(1, 2), (2, 3), (3, 4), (2, 1)}
It is not a function because element 2 corresponds to two elements 3 and 1.

(ii) {(a, 0), (b, 0), (c, 1), (d, 1)}
It is a function because under this each element corresponds to one and only one element.

(iii) {(1, a), (2, b), (1, b), (2, a)}
It is not a function because element 1 corresponds to two elements a and b.

(iv) {(a, a), (b, b), (c, c)}
It is a function because first element of ordered pair set is not same.

(v) {a, b}
It is a function because a corresponds to b

(vi) {(4, 1), (4, 2), (4, 3), (4, 4)}
It is not a function because first element of ordered pair set is same.

(vii) {(1, 4), (2, 4), (3, 4), (4, 4)}
It is a function because first element of ordered pair set is unequal.

(viii) {(x, y) : x, y ∈ R, y2 = x}
Here y2 = x ⇒ y = ±√x and if x = 4 then y = ±2
Hence, element ofy is related with 2 and -2 so, it is not a function.

(ix) {(x, y) : x, y ∈ R, x2 = y}
It is a function because for y = x2, each real value of x there is a unique image in R for each element of R

(x) {(x, y) : x, y ∈ R, x = y3}
It is a function because y = x1/3, ∀ x ∈ R unique image is the set B.

(xi) {(x, y) : x, y ∈ R, y = x3}
It is also a function because for y = x3 ∀ x ∈ R unique image is in set B.

Question 2.
If f : R → R, f(x) = x2, then find
(i) Range of f,
(ii) {x | f(x) = 4},
(iii) {y | f(y) = -1}
Solution:
(i) Given, f : R → R
and f(x) = x2
then if x < 0 ⇒ x2 > 0
x = 0 ⇒ x2 = 0
x > 0 ⇒ x2 > 0
So, f(x) = x2 ≥ 0 ∀ x ∈ R
Hence, range of R = R+ ∪ {0} or {x ∈ R | 0 ≤ x < ∞}
(ii) f(x) = 4
⇒ x2 = 4
⇒ x = ±2
Hence, {x : y (x) = 4} = {-2, 2}.
(iii) f(y) = -1
⇒ y2 = -1
⇒ y = ±√1
⇒ (y : f(y) = -1} = Φ null set.

Question 3.
Let A = {-2, -1, 0, 1, 2} and function f is defined in A to R by f(x) = x2 + 1. Find the range of f.
Solution:
Given, A = {-2, -1, 0, 1, 2}
and R = set of real numbers
Given: f(x) = x2 + 1
then f(-2) = (-2)2 + 1 = 5
f(-1) = (-1)2 + 1 = 2
f(0) = (0)2 + 1 = 1
f(1) = (1)2 + 1 = 2
f(2) = (2)2 + 1 = 5
Hence, range of f = (1, 2, 5}.

Question 4.
Let A = {-2, -1, 0, 1, 2} and f : A → Z where f(x) = x2 + 2x – 3, then find
(i) Range of f
(ii) Pre image of 6, -3 and 5
Solution
(i) Given,
A = {-2, -1, 0, 1, 2} and Z = {0, ± 1, ± 2, …}
from f(x) = x2 + 2x – 3
f(-2) = (-2)2 + 2(-2) – 3 = 4 – 4 – 3 = -3
f(-1) = (-1)2 + 2(-1) – 3 = 1 – 2 – 3 = – 4
f(0) = 02 + 2(0) – 3 = -3
f(1) = 12 + 2(1) – 3 = 1 + 2 – 3 = 0
f(2) = (2)2 + 2(2) – 3 = 4 + 4 – 3 = 5
Hence, Range of f = set of f(x) = {-4, -3, 0, 5}
(ii) Let pre-image of 6 is x
f(x) = 6
⇒ x2 + 2x – 3 = 6
⇒ x2 + 2x – 9 = 0
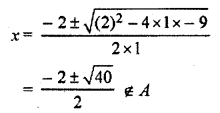
RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 1
As there is no pre-image of 6 in A.
Hence, pre-image of A is Φ
Again, let the pre-image of A be -3 in x, then
f(x) = -3
⇒ x2 + 2x – 3 = -3
⇒ x2 + 2x = 0
⇒ x(x + 2) = 0
⇒ x = 0, x = – 2
Hence, pre-image of A in -3 is -2 or 0 {-2, 0}
Similarly to find the pre-image of 5
f(x) = 5
⇒ x2 + 2x – 3 = 5
⇒ x2 + 2x – 8 = 0
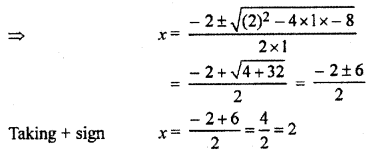
RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 2
RBSE Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 3
The domain of the signum function is the set of real numbers and the range is {-1, 0, 1}.

RBSE Solutions for Class 11 Maths