Rajasthan Board RBSE Class 11 Maths Chapter 2 Relations and Functions Ex 2.4
Question 1.
Classify the following functions is the form of one-one, many one, into and onto, also give reason to support your answer.
(i) f : Q → Q, f(x) = 3x + 7
(ii) f : C → R, f(x + iy) = x
(iii) f : if R → [-1, 1], f(x) = sin x
(iv) f : N → Z, f(x) = |x|
Solution:
(i) Given f : Q → Q and f(x) = 3x + 7
where Q is set of rational numbers.
Let x1, x2 ∈ Q are in this way f(x1) = f(x2)
f(x1) = f(x2)
⇒ 3x1 + 7 = 3x2 + 7
⇒ 3x1 = 3x2
⇒ x1 = x2
⇒ f(x1) = f(x2)
⇒ x1 = x2
x1, x2 ∈ Q
Hence, f is one-one function.
Now, Let y ∈ Q co-domain
If possible, then let pre-image of y is x in domain Q then
f(x) = y
⇒ 3x + 7 = y
⇒ x = \(\frac { y-7 }{ 3 }\) ∈ Q
So, every element in the co-domain of Q has pre-image in Q
Hence, f is onto function.
Thus, f is a one-one, onto function.
Use our Domain and Range Calculator tool to get the domain and range for your function. Also, get steps to check the domain and range for any type of function
(ii) f : C → R : f(x + iy) = x
Given : function
f : C → R and f(x + iy) = x
Here C = set of complex numbers
R = set of real numbers
Let x + iy and x – iy (y ≠ 0) are different elements in domain C.
f(x + iy) = x and f (x – iy) = x
⇒ f(x + iy) = f(x – iy)
So, two different elements of domain R have the same image.
So, f is a many-one function.
Here Range of f = (x : x + iy ∈ C} – R Co-domain
[Range of x + iy in x ∈ R, y ∈ R and i = √-1 ]
f is a onto function.
Thus, f is a many-one, onto function.
(iii) f : R → [-1, 1], f(x) = sin x
Given: f : R → [-1, 1] and f(x) = sinx
where R is set of real numbers.
Let x1, x2 ∈ R
If f(x1) = f(x2) ⇒ sin x1 = sin x2
⇒ x1 = nπ + (-1)nx2, n ∈ I (General value of sin θ)
⇒ x1 ≠ x2
f is not one-one function so, it is many-one function
Again, Let y ∈ Y
If possible then let pre-image of y under f is x then
f(x) = y
⇒ sin x = y
⇒ x = sin-1y
So, -1 ≤ y ≤ 1
Many value of sin-1y present in R, then
x ∈ R ∀ y ∈ [-1, 1]
f is onto function.
Thus, f is many-one, onto function.
(iv) f : N → Z, f(x) = |x|
Given f : N → Z and f(x) = |x|
where N = Set of natural number = {1, 2, 3, 4,…}
and Z = set of natural numbers = {0, ± 1, ± 2, ± 3, …}
Let x1, x2 ∈ N
If f(x1) = f(x2) ⇒ |x1| = |x2| [∵ x1 > 0, x2 > 0, x1, x2 ∈ N]
⇒ x1 = x2
f is one-one function.
Again ∵ Range of f = {|x| : x ∈ N], Z ≠ Z (co-domain)
So, f is not onto function.
Hence, f is into function.
Thus, f is one-one into function.
Question 2.
If A = {x | -1 ≤ x ≤ 1} = B, then find out which function is one-one, into or one-one onto defined from A to B
(i) f(x) = \(\frac { x }{ 2 }\)
(ii) g(x) = |x|
(iii) h(x) = x2
(iv) k(x) = sinπx
Solution:
Given equation
A = {x : -1 ≤ x ≤ 1)
and B ={x : -1 ≤ x ≤ 1}
(i) Function is defined from A to B.
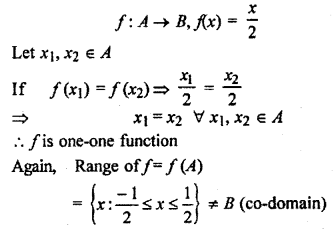
f is not onto function.
Hence, it is proved that f is one-one, into function,
(ii) g : A → B, g (x) = |x|
Let x1, x2 ∈ A
If f(x1) = f(x2)
⇒ g(x1) = g(x2)
⇒ |x1| = |x2|
⇒ x1 = ±x2
g is not one-one function so, g is many one function.
Again, range of g = { x : -1 ≤ x ≤ 1} ≠ B (co-domain)
i.e., pre-image of negative number is not exist in codomain B.
Thus, it is proved that f is many-one, into function.
g is not one-one function.
(iii) h : A → B, h(x) = x2
Let x1, x2 ∈ A.
Thus, h(x1) = h(x2)
h (x1) = h (x2)
⇒ x12 = x22
⇒ x1 = ± x2
h is not one-one function.
For example 1 ≠ -1 but h(1) = h(-1) = 1
So, h is a many-one function.
Let y ∈ B if possible pre-image of y is x exist in B, then
h(x) = y
⇒ x2 = y
⇒ x = ±√y
when y is positive then, x does not exist
i.e., pre-image of a negative number does not exist.
So, Range of h ={x : 0 ≤ x ≤ 1} ≠ B (co-domain)
So, h is a into function
Hence, it is proved that h is many-one, into function,
(iv) k : A → B, k(x) = sin πx
-1, 1 ∈ A are such numbes
-1 ≠ 1
But k(-1) = sin (-π) = 0
⇒ k(1) = sin π = 0
So, -1 ≠ 1
⇒ k(-1) = k(1)
i.e., different elements have same image.
k is many-one function.
Again, range of k = {sin πx : x ∈ A} = {x : -1 ≤ x ≤ 1} = B (co-domain)
k is onto function
Hence, it is proved that k is many-one, onto function.
Question 3.
If f : C → C, f(x + iy) = (x – iy), then prove that f is an one-one onto function.
Solution:
Given : f : C → C and f(x + iy) = x – iy
where C is set of complex numbers.
Let x1 + iy1 and x2 + iy2 ∈ C thus.
f(x1 + iy1) = f (x2 + iy2)
⇒ x1 – iy1 = x2 – iy2
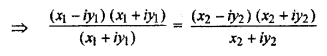
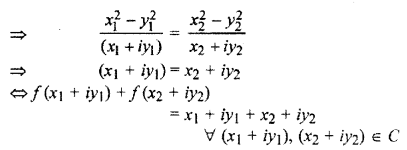
So, f is one-one function.
Range of f = {x – iy : x + iy ∈ C} = C (co-domain)
f is onto function.
Hence, f is one-one, onto function.
Hence Proved.
Question 4.
Give one example of each of the following function:
(i) One-one into
(ii) Many-one onto
(iii) Onto but not one-one
(iv) One-one but not onto
(v) Neither one-one nor onto
(vi) One-one onto
Solution:
(i) f : N → N, f(x) = 2x
(ii) f : R0 → R+, f(x) = x2
(iii) f : z0 → N, f(x) = |x|
(iv) f : Z → Z, f(x) = 2x
(v) f : R → R1, f(x) = x2
(vi) f : Z → f(z) = -x
Question 5.
Prove that f : R → R, f(x) = cos x is a many- one into function. Change the domain and co-domain of f such that I become:
(i) One-one into
(ii) Many-one onto
(iii) One-one onto
Solution:
Given, f : R → R, f(x) = cos x
Let x1, x2 ∈ R
Thus, f(x1) = f(x2)
f(x1) = f(x2)
⇒ cos x1 = cos x2
⇒ x2 = 2nπ ± x2, x1 ∈ I
f is not one-one function.
Again, let, y ∈ R (co-domain), if possible let pre-image of y is x is domain R, then
f(x) = y
⇒ cos x = y
⇒ x = cos-1y
x only exist when,
-1 ≤ y ≤ 1
when y ∈ R – [-1, 1]
Pre-image of y is not present in domain R.
So, f is not onto function
Hence, f is many-one, into function.
(i) One-one, into function
f : [0, π] → R, f(x) = cos x
(ii) Many-one, onto function
f : R → [-1, 1], f(x) = cos x
(iii) One-one, onto function.
f : [0, π] → [-1, 1], f(x) = cos x
Question 6.
If N= {1, 2, 3, 4, …), O = (1, 3, 5, 7, …}, E = (2, 4, 6, 8,…..) and f1, f2 are function defined as
f1 : N → O, f1(x) = 2x – 1; f2 : N → E, f2(x) = 2x
Then prove that f1 and f2 are one-one onto.
Solution:
(i) Given N = {1, 2, 3, …}
O = {1, 3, 5, …}
Function f(x) = 2x – 1
Let x1, x2 ∈ N
Thus f(x1) = f(x2)
f(x1) = f(x2)
⇒ 2x1 – 1 = 2x2 – 1
⇒ 2x1 = 2x2
⇒ x1 = x2 ∀ x1, x2 ∈ N
So, f1 is one-one function.
Again, let y ∈ O (co-domain), if possible let pre-image of y is x exist in domain N, then f(x) = y.
f(x) = y
⇒ 2x – 1 = y
⇒ x = \(\frac { y+1 }{ 2 }\) ∈ N ∀ y ∈ O
So, pre-image of every element of O (co-domain) exist in domain N
So, f1 is onto function.
Hence, f is one-one onto function
(ii) Given set are
N = {1, 2, 3, …}
E = {2, 4, 6, …}
Function f2 : N → E, f2(x) = 2x ∀ x ∈ N
Let x1, x2 ∈ N
Thus f2(x1) = f2(x2)
f2(x1) = f2(x2)
⇒ 2x1 = 2x2
⇒ x1 = x2 ∀ a, b ∈ N
f2 is one-one function.
Again, let y ∈ E (co-domain), if possible, let pre-image of y is x exist in domain N then f2(x) = y
f2(x) = y
⇒ 2x = y
⇒ x = \(\frac { y }{ 2 }\) ∈ N ∀ y ∈ E
So, pre-image of every element of E (co-domain) exist in domain N.
Hence, f2 is one-one, onto function.
Question 7.
If function f is defined from set of real numbers R to R in the following way then classify them in the form of one-one, many-one, into or onto.
(i) f(x) = x2
(ii) f(x) = x3
(iii) f(x) = x3 + 3
(iv) f(x) = x3 – x
Solution:
(i) Given, f : R → R, f(x) = x2
where, R is set of real number
Let x1, x2 ∈ R
Thus f (x1) = f (x2)
f(x1) = f(x2)
⇒ x12 = x22
⇒ x1 = ±x2
f is not one-one function. So, f is many-one function.
Let y ∈ R (co-domain), if possible, let pre-image of y is x in domain R, then f(x) = y
f (x) = y
⇒ x2 = y
⇒ x = ±√y
If is clear, x is not exist for negative values of y.
So, f is into function.
Hence, f is many-one into function.
(ii) Given: f : R → R and f(x) = x3
Let x1, x2 ∈ R
Thus f(x1) = f(x2)
f(x1) = f(x2)
⇒ x13 = x23
⇒ x1 = x2 ∀ x1, x2 ∈ R
f is one-one function
Again, let y ∈ R (co-domain), if possible, let pre-image ofy is x in domain R, then
f (x) = y
f(x) = y
⇒ x3 = y
⇒ x = y1/3 ∈ R
So, f is onto function.
Hence, f is one-one onto function.
(iii) Given: f : R → R and f(x) = x3 + 3
Where R is set of real number
Let x1, x2 ∈ R
Thus f (x1) = f(x2)
f(x1) = f(x2)
⇒ x13 + 3 = x22 + 3
⇒ x13 = x23 ∀ x1, x2 ∈ R
So, f is one-one function.
Again let y ∈ R (co-domain)
If possible, let pre-image of y is x in f then
f (x) = y
⇒ x3 + 3 = y
⇒ x = (y – 3)1/3 ∈ R ∀ y ∈ R
So, pre-image of every element R (co-domain) is exist in domain R.
Hence, f is one-one, onto function.
(iv) Given: f : R → R, f(x) = x3 – x
Where R is set of real numbers.
Let 0, 1 ∈ R are such numbers
0 ≠ 1
0 ∈ R ⇒ f(0) = 0 – 0 = 0
1 ∈ R ⇒ f(1) = 13 – 1 = 0
0 ≠ 1 and f(0) = f(1) = 1
So, f is many-one function.
Again, range of f = f(R) = {x3 – x : x ∈ R) = R (domain)
So, f is onto function
Hence, f is many-one, onto function.