Rajasthan Board RBSE Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.1
Question 1.
Find the radian measures corresponding to the following degree measures
(i) 25°
(ii) -47°30′
(iii) 520°
Solution :

Question 2.
Find the degree measures corresponding to the following radian measures \(\left( use\pi =\frac { 22 }{ 7 } \right) \)
(i) \(\frac { 11 }{ 16 } \)
(ii) -4
(iii) \(\frac { 5\pi }{ 3 } \)
Solution:
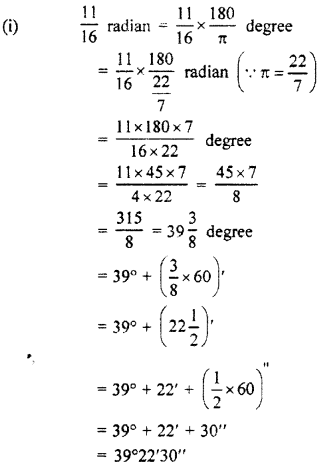
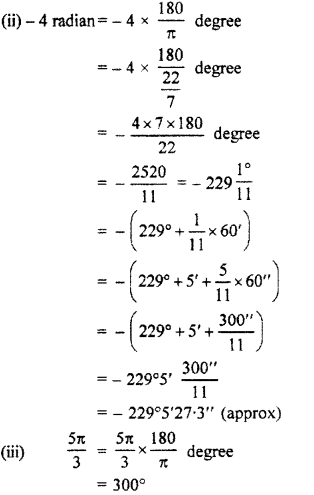
Question 3.
A wheel makes 360 revolutions in 1 minute than how many radians does it turn in one second ?
Solution:
∵ The wheel revolves 360 times in 1 minute, So, in 60 second there are 360 revolution, then
In 1 Second = 360° / 60 = 6 revolution
Angle make in 1 revolution = 2π radian
then angle make in 6 revolution
= 6 x 2π radian
= 12π radian
Hence, angle make in 1 second by the wheel
= 12π radian
Question 4.
Find the degree measure of the angle sub¬tended at the centre of a circle of radius 100 cm by an are of length 22 cm \(\left( use\pi =\frac { 22 }{ 7 } \right) \)
Solution :
Radius of circle ( r ) = 100 cm
length of arc ( l ) – 22 cm
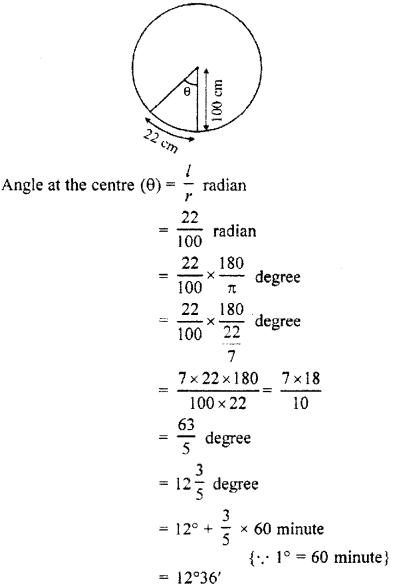
Hence, the angle subtended at the centre of the circle is = 12°36′
Question 5.
In a circle of diameter 40 cm, the length of a chord is 20 cm. Find the length of minor arc of corresponding chord.
Solution:
Diameter of circle = 40 cm
Radius of circle (r) = 20 cm
Let AB is a chord of the circle, whose length is 20 cm.
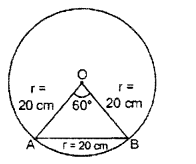
After joining A and B to centre of circle O.
We get an equilateral triangle ΔOAB
Hence, angle at the centre
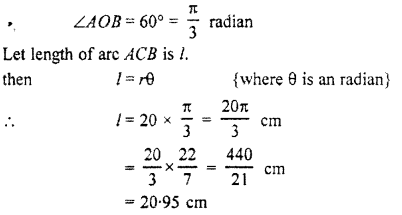
Hence, the length of minor arc of corresponding chord is
\(\frac { 20\pi }{ 3 } \) cm or 20.95 cm
Question 6.
If in two circles, arcs of the same length subtend angles of 60° and 75° at the centre, find the ratio of their radii.
Solution:
Let radii of circle r1 and r2.
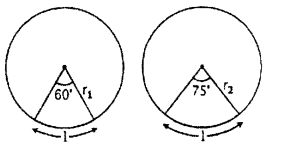
then angle substened by an arc at the centre of first circle is
θ = 60° = \(\frac { \pi }{ 3 } \) radian
Angle subtended by an arc at the centre of second circle is
= 75° = \(\frac { 75\pi }{ 180 } \) = \(\frac { 5\pi }{ 12 } \)
From fomula : Length of arc ( l )
= radius (r) x angle (θ)
∴ Length of arc of first circle = \(\frac { \pi }{ 3 } \) x r1
Length of arc of second circle = \(\frac { 5\pi }{ 12 } \) x r2
Given that: Arcs of two circles are of same length
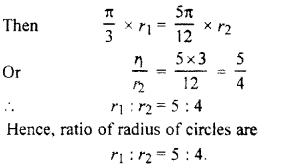
Question 7.
Find the angle in radian through which a pendulum swings, if its length is 75 cm and the tip describes an arc of length
(i) 10 cm
(ii) 21 cm
Solution:
(i) Length of pendulum ( r ) = 75 cm
Length of arc ( l ) = 10 cm
Let pendulum makes an angle θ
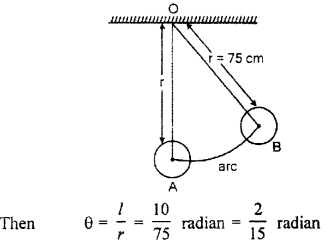
Hence, angle make by swings pendulum = \(\frac { 2 }{ 15 } \) radian
(ii) Length of pendulum ( r ) = 75 cm
length of arc ( l ) = 21 cm
Let pendulum makes an angle θ
θ = \(\frac { l }{ r } \) = \(\frac { 21 }{ 5 } \) = \(\frac { 7 }{ 25 } \) radian
Hence, angle makes by swings pendulum
= \(\frac { 7 }{ 25 } \)