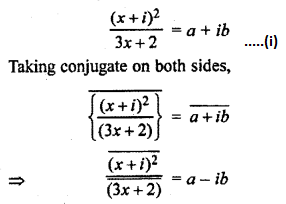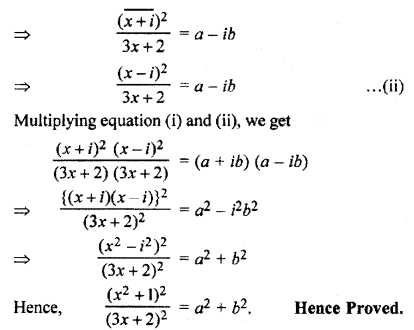Rajasthan Board RBSE Class 11 Maths Chapter 5 Complex Numbers Ex 5.1
Question 1.
Write the following in simplest form:
(i) i52
(ii) √-2 √-3
(iii) (1 + i)5 (1 – i)5
Solution:

Question 2.
Find the additive and multiplicative inverse of following numbers:
(i) 1 + 2i
(ii) 1/(3 + 4i)
(iii) (3 + i)2
Solution:
(i) Let z = 1 + 2i
Then additive inverse = -z = -(1 + 2i) = -1 – 2i
And multiplicative inverse = \(\frac { 1 }{ z }\)
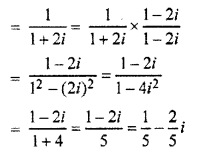


Question 3.
Find the conjugate number of complex number \(\frac { \left( 2+i \right) ^{ 3 } }{ 3+i }\)
Solution:
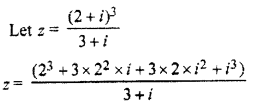
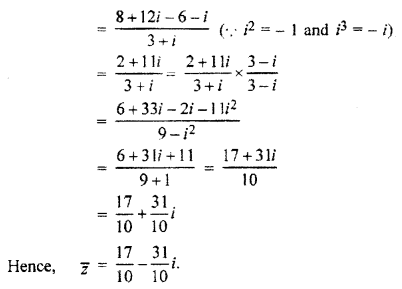
Question 4.
Find the modulus of the following:
(i) 4 + i
(ii) -2 – 3i
(iii) 1/(3 – 2i).
Solution:


Question 5.
If a2 + b2 = 1 then find the value of \(\frac { 1+b+ia }{ 1+b-ia }\)
Solution:
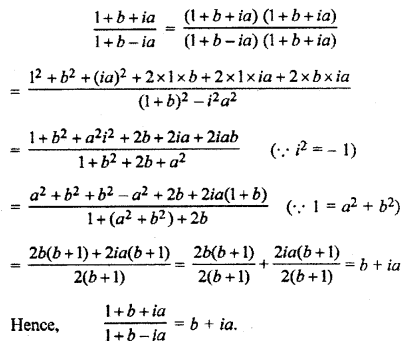
Question 6.
If a = cos θ + i sin θ, then find the value of \(\frac { (1+a) }{ (1-a) }\)
Solution:
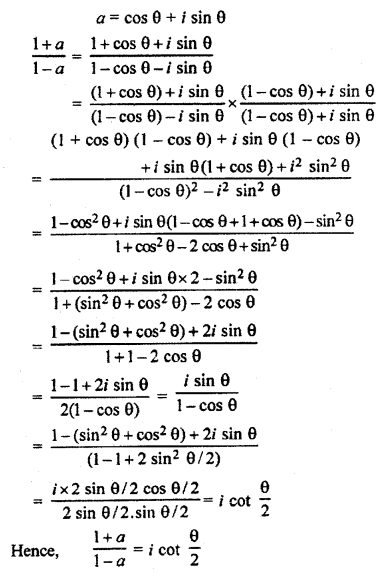
Question 7.
Find the value of x and y which satisfy the equation
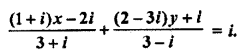
Solution:
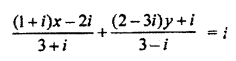
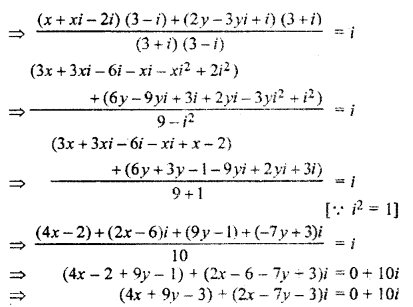
Comparing the real and imaginary part on both sides
4x + 9y – 3 = 0 and 4x + 9y = 3 …..(i)
2x – 7y – 3 = 10 and 2x – 7y = 13 ……(ii)
Solving equation (i) and (ii), we get
x = 3 and y = -1
Question 8.
If z1 and z2 are any two complex numbers, then prove that
|z1 + z2|2 + |z1 – z2|2 = 2|z1|2 + 2|z2|2.
Solution:
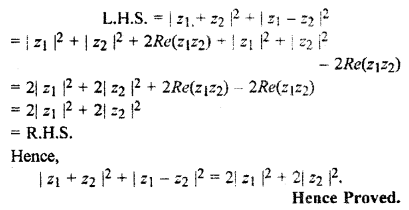
Question 9.
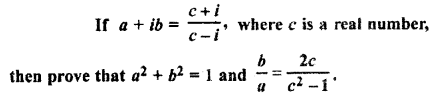
Solution:
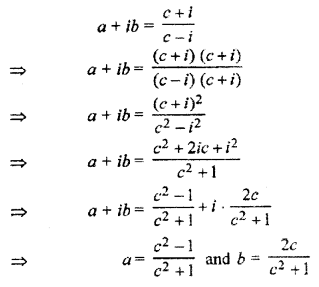

Question 10.
If (x + iy)1/3 = a + ib, then prove that \(\frac { x }{ a }\) + \(\frac { y }{ b }\) = 4(a2 – b2).
Solution:
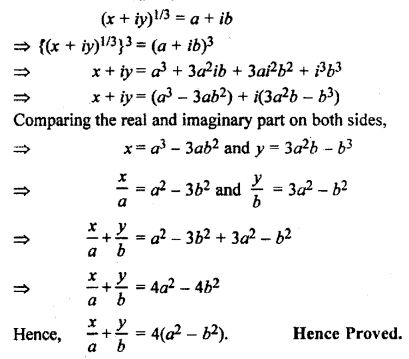
Question 11.
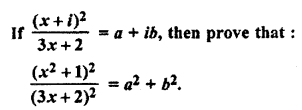
Solution: