Rajasthan Board RBSE Class 11 Maths Chapter 5 Complex Numbers Ex 5.4
Question 1.
Find the solution of following equations by vedic method
(i) x2 + 4x + 13 = 0
(ii) 2x2 + 5x + 4 = 0
(iii) ix2 + 4x – 15/2 = 0
Solution:
(i) Given equation
x2 + 4x + 13 = 0
Comparing this equation with ax2 + bx + c = 0, we get
a = 1, b = 4, c = 13
First derivative = Discriminant

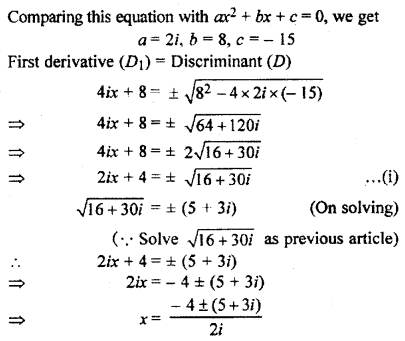
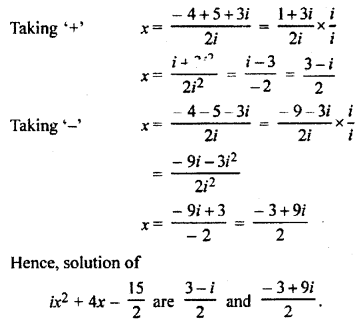
Question 2.
Find quadratic equation which has the following roots
(i) 5 and -2
(ii) 1 + 2i
Solution:
(i) root α = 5 and β = – 2
Then, sum of roots = α + β = 5 – 2
⇒ α + β = 3
and product of roots = αβ = 5 × (-2)
⇒ αβ = -10
Hence, required equation whose roots are 5 and -2.
x2 – (sum of roots) x + product of roots = 0
⇒ x2 – 3x + (-10) = 0
⇒ x2 – 3x – 10 = 0
Hence, required equation is x2 – 3x – 10 = 0 whose roots are 5 and -2.
(ii) Roots α = 1 + 2i and β = 1 – 2i
Then, sum of roots α + β = 1 + 2i + 1 – 2i = 2
and product of roots αβ = (1 + 2i)(1 – 2i) = 1 – 4i2 = 1 + 4 = 5
Hence, required equation whose roots are 1 + 2i and 1 – 2i,
x2 – (sum of roots) x + Product of roots = 0
⇒ x2 – 2x + 5 = 0.
Remark: If one root is 1 + 2i, then second not will be 1 – 2i.
Question 3.
If one root of equation x2 – px + q = 0 is twice the other then prove that 2p2 = 9q.
Solution:
Given equation
x2 – px + q = 0
Let its roots be α and β, then
According to question α = 2β then

Question 4.
Find that condition for which equation ax2 + bx + c = 0 has roots in the ratio m : n.
Solution:
Given equation,
ax2 + bx + c = 0
Let its roots be α and β, then
According to question,
α : β = m : n

