RBSE Solutions for Class 11 Maths Chapter 5 Complex Numbers Miscellaneous Exercise

Rajasthan Board RBSE Class 11 Maths Chapter 5 Complex Numbers Miscellaneous Exercise

Question 1.
Real and imaginary parts of complex number \(\frac { 1+i }{ 1-i }\) respectively are:
(A) 1, 1
(B) 0, 0
(C) 0, 1
(D) 1, 0
Solution:

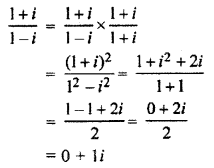
Real part = 0
Imaginary part = 1
Hence, option (C) is correct.

Question 2.
If 2 + (2a + 5ib) = 8 + 10i, then:
(A) a = 2, b = 3
(B) a = 2, b = -3
(C) a = 3, b = 2
(D) a = 3, b = -2
Solution:
2 + (2a + 5ib) = 8 + 10i
⇒ (2 + 2a) + 5bi = 8 + 10i
On comparing
2 + 2a = 8
⇒ 2a =6
⇒ a = 3
and 5b = 10
⇒ b = 2
So, a = 3 and b = 2
Hence, option (C) is correct.

Question 3.
The multiplicative inverse of 3 – i is:

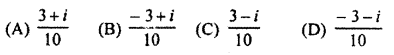
Solution:
Let z = 3 – i
Let multiplicative inverse of z

Question 4.

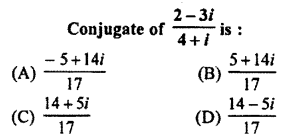
Solution:

Question 5.
If z₁, z₂ ∈ C then which statement is true:
(A) |z₁ – z₂| ≥ |z₁| + |z₂|
(B) |z₁ – z₂| ≤ |z₁| + |z₂|
(C) |z₁ + z₂| ≥ |z₁ – z₂|
(D) |z₁ + z₂| ≤ |z₁ – z₂|
Solution:
statement |z₁ – z₂| ≤ |z₁| + |z₂| is true.
Hence, option (B) is correct.

Question 6.
If |z – 3| = |z + 3|, then z lies in
(A) at x-axis
(B) at y-axis
(C) on line x = y
(D) on line x = -y
Solution:
Let z = x + iy

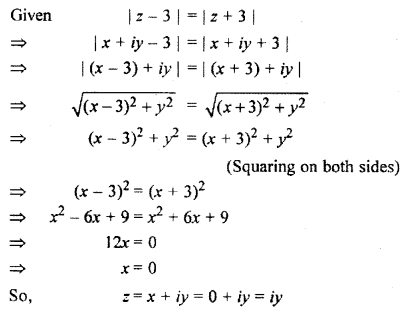
It is situated on the axis.
Hence, option (B) is correct.

Question 7.
Write the principal argument of -2.
Solution:
-2 = -2 + 0i
Let -2 + 0i = r(cos θ + i sin θ)
⇒ r cos θ = -2 ….(i)
r sin θ = 0 ………(ii)
⇒ tan θ = \(\frac { 0 }{ -2 }\) = 0
Hence, principal arument of -z is π.

Question 8.
Write polar form of \(\frac { 5\surd 3 }{ 2 } +\frac { 5 }{ 2 } i\)
Solution:

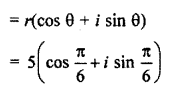
Question 9.
What is the value of 4 + 5ω⁴ + 3ω⁵?
Solution:

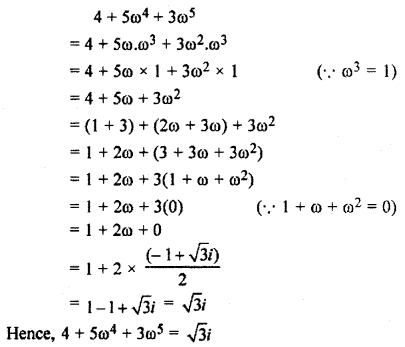
Question 10.
Write \(\frac { 1 }{ 1-cos\theta +isin\theta }\) in the form of a + ib.
Solution:

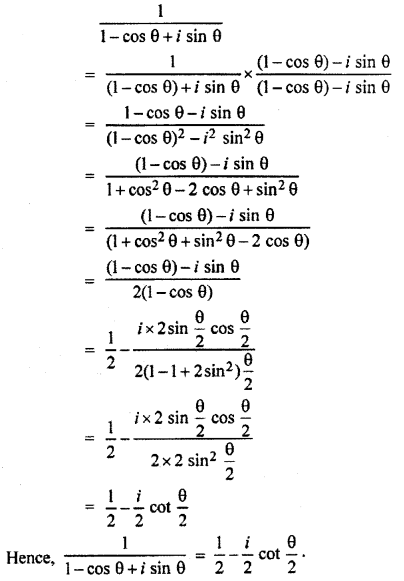
Question 11.
What is the number of non-zero integer roots of |1 – i|^x = 2^x?
Solution:

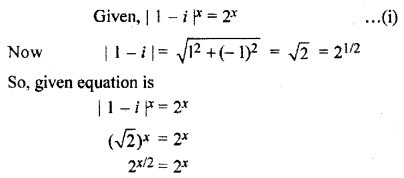
Comparing power of both sides
\(\frac { x }{ 2 }\) = x, which is not possible (because x is not zero)
Thus, the root of equation |1 – i|^x = 2^x is not possible.
Hence, the number of roots is zero.

Question 12.
If z₁, z₂ ∈ C prove that
(i) |z₁ – z₂| ≤ |z₁| + |z₂|
(ii) |z₁ + z₂| ≥ |z₁| – |z₂|
(iii) |z₁ + z₂ + ….. + z_n| ≤ |z₁| + |z₂| + ……. + |z_n|
Solution:

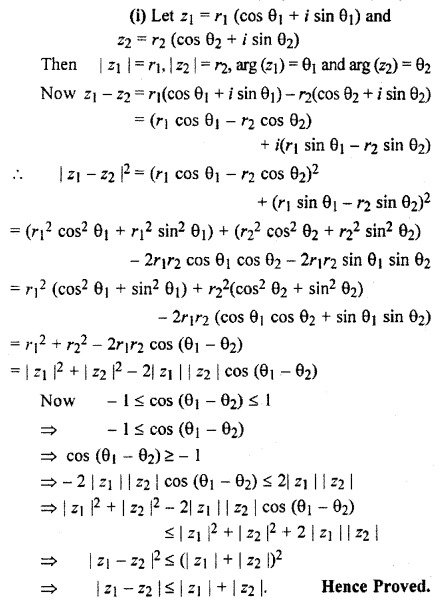
Question 13.
If |z₁| = 1 = |z₂| then prove that

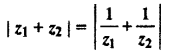
Solution:
According to question,

Question 14.

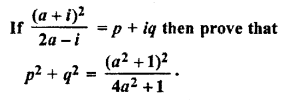
Solution:

Question 15.
If |z₁| = |z₂| and arg z₁ + arg z₂ = 0 then prove that z₁ = \(\bar { { z }_{ 2 } }\).
Solution:

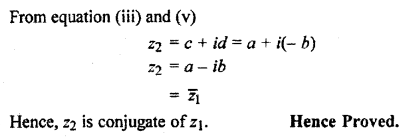
Question 16.
If θ₁ and θ₂ are arguments of complex numbers z₁ and z₂ respectively then prove that:
z₁\(\bar { { z }_{ 2 } }\) + \(\bar { { z }_{ 1 } }\)z₂ = 2|z₁||z₂| cos(θ₁ – θ₂)
Solution:

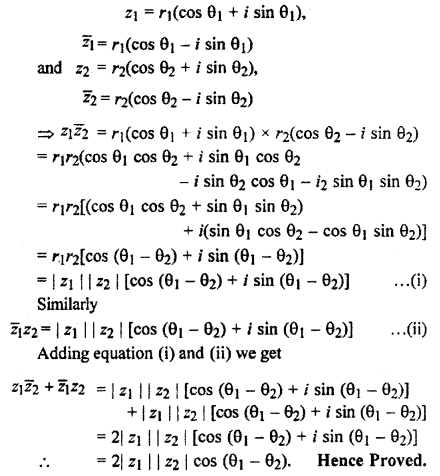
Question 17.
Prove that:
(i) (a + bω + cω²) (a + bω² + cω) = a² + b² + c² – ab – bc – ca
(ii) (a + b + c) (a + bω + cω²) (a + bω² + cω) = a³ + b³ + c³ – 3abc
Solution:

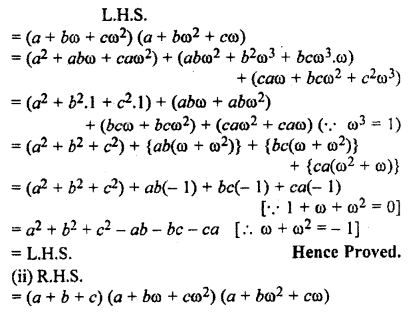
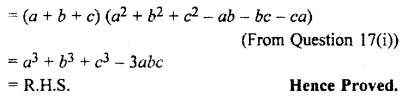
Question 18.
If α, β are two complex numbers and |β| = 1 then prove that \(\left| \frac { \beta -\alpha }{ 1-\bar { \alpha } \beta } \right| =1\)
Solution:

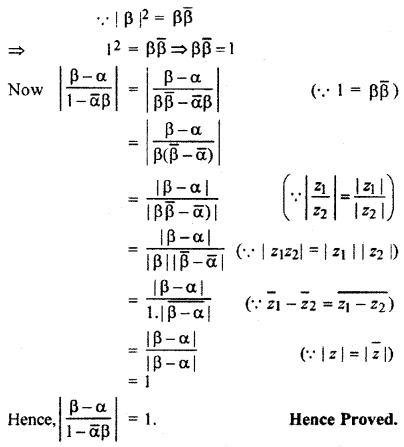
Question 19.
If α and β roots of equation px² – qx – r = 0, then find the equation which has roots 1/α and 1/β
Solution:
α, β are roots of equation px² – qx – r = 0

⇒ rx² + qx – p = 0
Hence, required equation is rx² + qx – p = 0

Question 20.
Find conditions for which equation lx² – 2mx + n = 0 has roots such that one root is P times the other roots.
Solution:
Given equation lx² – 2mx + n = 0
Let it’s one root is a and another root is Pα.
Then, the sum of roots

RBSE Solutions for Class 11 Maths