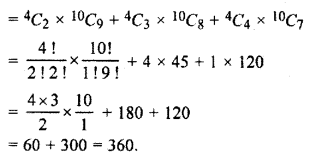RBSE Solutions for Class 11 Maths Chapter 6 Permutations and Combinations Ex 6.2

Rajasthan Board RBSE Class 11 Maths Chapter 6 Permutations and Combinations Ex 6.2

Question 1.
Find the value of n, whereas:

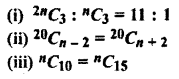
Solution:

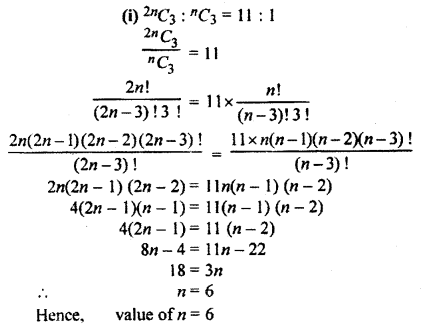
Question 2.
Find the value of ⁵⁰C₁₁ + ⁵⁰C₁₂ + ⁵¹C₁₃ – ⁵²C₁₃.
Solution.

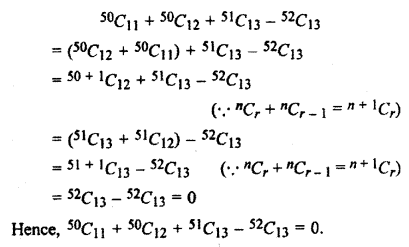
Question 3.
In a triangle ABC, there are 3, 4 and 5 points on side AB, BC, CA respectively. How many triangles will be formed by these points?
Solution:
Total number of points on side AB, BC and CA = 3 + 4 + 5 = 12
Hence, number of triangles formed by 12 points


Points on sides AB, BC and CA are collinear.
Hence, any triangle cannot be formed by these points
Hence, total number of required triangles = 220 – 1 – 4 – 10 = 205.

Question 4.
A box contains two white, three black and four red balls. Determine the number of ways in which three balls can be selected from this box, in which at least one black ball is compulsory.
Solution:
Total number of balls in the box = 2 + 3 + 4 = 9
For at least one black ball we can choose it in the following ways.

Question 5.
By 6 different coloured flags, taking one or more than one how many ways signal can be given?

Solution:
Total number of coloured flags = 6
Hence we can take any colour from 1 to 6.
Thus, the number of signals formed by using 6 different types of coloured flags

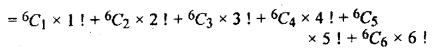
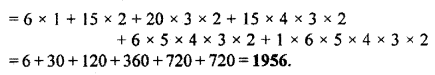
Question 6.
Number of diagonals in a polygon is 44 then find a number of its sides.
Solution:
Number of diagonals = 44
Formula : Number of diagonals = \(\frac { n(n-3) }{ 2 }\)
where n = number of sides.
⇒ \(\frac { n(n-3) }{ 2 }\) = 44
⇒ n² – 3n = 88
⇒ n² – 3n – 88 = 0
On solving n = 11, -8
Negative number is not possible.
Hence, the number of sides = 11.

Question 7.
How many numbers can be formed taking 4 digits from digits 1, 2, 3, 4, 5, 6 whereas digit 4 and 5 are compulsory?
Solution:
Total number of digits = 6
We Have to take 4 digits but digit 4 and 5 are compulsory.
Thus, we have to choose only 2 digits out of 6 – 2 = 4 digits.
Now, the numbers formed by using 4 digits is ⁴P₄.
Hence required number

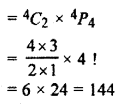
Question 8.
In how many ways 6 ‘+’ and 4 ‘-‘ sign can be kept in a line whereas any two ‘-‘ occur together?
Solution:
First we put ‘+’ in a line. This can be done in 1 way because all ‘+’ are same.
+ + + + + +
Now we put ‘-‘ in the following way
– + – + – + – + – + – + –
Hence, the method of putting ‘-‘ sign in 4 out of 7 places = ⁷C₁ × 1 because ‘-‘ signs are same.
Total number of ways 6 ‘+’ and 4 ‘-‘ sign occur together

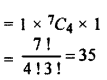
Question 9.
By 8 students and 5 professors, we have to make a college council, taking 5 students and 2 professors. How many councils can be formed?
Solution:
Number of methods of choosing 5 out of 8 students = ⁸C₅
and number of methods of choosing 2 out at 5 professors = ⁵C₂
By the basic principle of calculation, the methods of choosing 5 out of 8 students and 2 out of 5 professors are

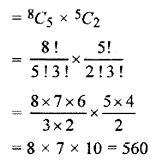
Hence required councils are 560.

Question 10.
In how many ways can one select a cricket team of 11 from 14 players in which at least 2 bowlers are compulsory whereas only 4 players can bowl. How many ways this team can be formed?
Solution:
The method of choosing 2 out of 4 bowlers is ⁴C₂ and the method of choosing 9 out of remains to players ¹⁰C₉. Similarly, we can find methods for 3 and 4 bowlers.
Hence, total number of ways to select 11 players out of 14 players

RBSE Solutions for Class 11 Maths