RBSE Solutions for Class 11 Maths Chapter 6 Permutations and Combinations Miscellaneous Exercise

Rajasthan Board RBSE Class 11 Maths Chapter 6 Permutations and Combinations Miscellaneous Exercise

Question 1.
If ⁿP_n-2 = 60, then n will be:
(A) 2
(B) 4
(C) 5
(D) 3
Solution:

Question 2.
ⁿP_r ÷ ⁿC_r is equal to:
(A) n!
(B) (n – r)!
(C) \(\frac { 1 }{ r! }\)
(D) r!
Solution:

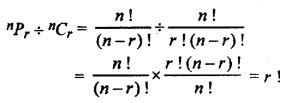
Hence, the option (D) is correct.

Question 3.
How many ways 5 persons can sit around the round table:
(A) 120
(B) 24
(C) 60
(D) 12
Solution:
Total number of ways to sitting 5 persons around the round table
= (5 – 1)! = 4!
= 4 × 3 × 2 × 1 = 24.
Hence, option (B) is correct.

Question 4.
How many words can be formed using letters BHILWARA:
(A) \(\frac { 8! }{ 2! }\)
(B) 8!
(C) 7!
(D) \(\frac { 6! }{ 2! }\)
Solution:
There are 8 letters in the given word in which 2 A’s and other letters are different.
Then numbers of words formed by letters of BHILWARA = \(\frac { 8! }{ 2! }\)
Hence option (A) is correct.

Question 5.

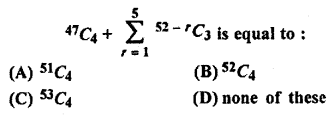
Solution:

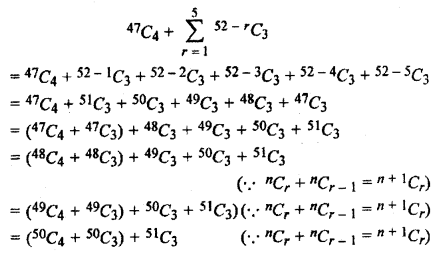
Question 6.
Find the value of ⁶¹C₅₇ – ⁶⁰C₅₆:
(A) ⁶¹C₅₈
(B) ⁶⁰C₅₇
(C) ⁶⁰C₅₈
(D) ⁶⁰C₅₆
Solution:

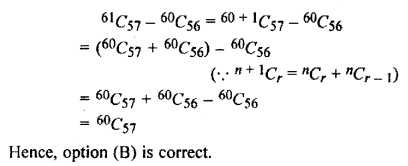
Question 7.
If ¹⁵C_3r = ¹⁵C_r+3, then r is equal to:
(A) 5
(B) 4
(C) 3
(D) 2
Solution

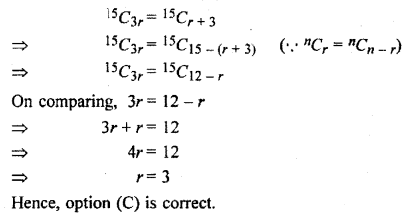
Question 8.
There are 6 points on the circumference of a circle, the number of straight lines joining their points will be:
(A) 30
(B) 15
(C) 12
(D) 20
Solution:
Number of lines passing through n points = ⁿC₂
Number of lines passing through 6 points

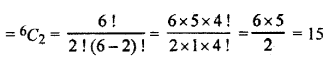
Hence, option (B) is correct.

Question 9.
How many words can be formed using letters of BHOPAL?
(A) 124
(B) 240
(C) 360
(D) 720
Solution:
Here, the number of letters are 6 and every time we take 6 letters.
Hence, required number of = ⌊6 = 6 × 5 × 4 × 3 × 2 × 1 = 720
Hence, option (D) is correct.

Question 10.
There are 4 points on the circumference of a circle by joining them how many triangles can be formed?
(A) 4
(B) 6
(C) 8
(D) 12
Solution:
There are three vertices in a triangle.
Given: There are 4 points on the circumference of a circle.
Then, the number of required triangles

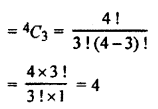
Hence, option (A) is correct.

Question 11.
If ⁿC₂ = ⁿC₇, then find ⁿC₁₆
Solution:

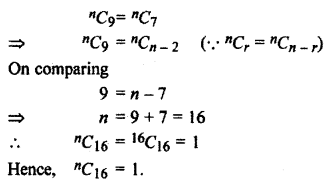
Question 12.
Find the value of n:
(i) ⁿC₂ : ⁿC₂ = 12 : 1
(ii) ²ⁿC₃ : ⁿC₃ = 11 : 1
Solution:

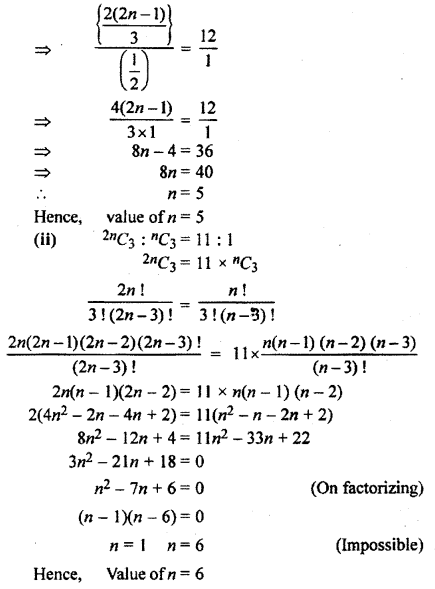
Question 13.
Find the number of chords passing through 11 points on the circumference of a circle.
Solution:
Number of the point on the circumference of circle = 11
We know that a chord is formed by joining two points.
Hence taking 2 points out of 11 points number of chords = ¹¹C₂

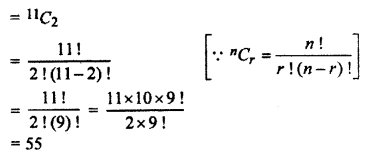
Hence, the number of chords = 55.

Question 14.
Determine the number of combinations out of deck of 52 cards of each selection of 5 cards has exactly one ace.
Solution:
Number of cards in a deck = 52
Total number of aces = 4
Hence Number of remaining cards = 52 – 4 = 48
We have to make a collection of 5 cards, in which there is 1 ace and 4 other cards.
Hence, number of ways choosing 1 out of 4 ace.
Now,Number of ways choosing 4 cards out of 48 cards

Total number of collection having 5 cards
= ⁴C₁ × ⁴⁸C₄ = 4 × 194580 = 778320
Hence, number of combinations formed by 5 cards = 778320.

Question 15.
There are n points in a plane in which m points are collinear. How many triangles will be formed by joining three points?
Solution:
For making a triangle we need three points thus if 3 points out of n points are not in a line, then ⁿC₃ triangle can be formed by n points but m point is in a line, thus ^mC₃ triangle forms less.
Hence, required number of triangles = ⁿC₃ – ^mC₃.

Question 16.
Find the number of diagonals of a decagon.
Solution:
There are 10 vertices in a decagon. Now by joining two vertices, we get a side of decagon or a diagonal.
Hence, the number of the line segment by joining of vertices of decagon = number of ways taking 2 points out of 10 points

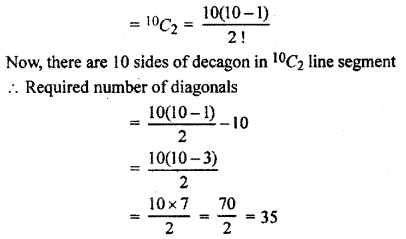
Hence, the number of diagonals is 35.

Question 17.
There are 5 empty seats in a train, then in how many ways three travellers can sit on these seats?
Solution:
A number of ways of seating of 3 travellers out of 5 seats.

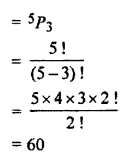
Hence, 3 travellers can be seated in 60 ways.

Question 18.
A group of 7 has to be formed from 6 boys and 4 girls. In how many ways a group can be formed if boys are in the majority in this group?
Solution:
Number of boys = 6
Number of girls = 4
Number of members in the group = 7
One putting boys in the majority in the group
We have to choose in the following ways :
4 boys + 3 girls
5 boys + 2 girls
6 boys + 1 girls
Number of ways choosing 4 boys and 3 girls = ⁶C₄ × ⁴C₃
Number of ways choosing 5 boys and 2 girls = ⁶C₅ × ⁴C₂
Number of ways choosing 6 boys and 1 girl = ⁶C₆ × ⁴C₁
Required number of ways forming the group

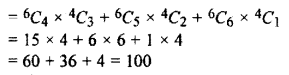
Hence, the group can be formed in 100 ways.

Question 19.
In the conference of 8 persons, every person handshake with each other only once, then find the total number of hand shook.
Solution:
When two persons shake hand with each other, then this is taken as one handshake.
Hence, the number of handshakes is equal to choosing 2 persons out of 8 persons.
Number of handshake

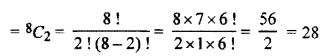
Hence, the required number of hand shaken is 28.

Question 20.
In how many ways 6 men and 6 women can sit around the round table whereas any two women never sit together?
Solution:
First, we sit the men in an order that there is a place vacant between two men.
Then, number of ways sitting 6 men = (6 – 1)! = 5!
Now a number of ways sitting 6 women in the vacant places = 6!
Number of permutations = (6 – 1)! = 5!
Now, the number of ways sitting 6 women in the vacant place = 6!
Number of permutaions = 5! × 6!
= (5 × 4 × 3 × 2 × 1) × (6 × 5 × 4 × 3 × 2 × 1)
= 86400.

Question 21.
In how many ways can the letters of the word ASSASSINATION be arranged so that all the S are together?
Solution:
Number of letters in word ASSASSINATION = 13
In this word A comes 3 times, S comes 4 times, I comes 2 times, N comes 2 times and other letters are different.
Now, taking 4’s together, then consider it as one letter, now adding other 9 letters and thus the permutation formed by 10 letters
= \(\frac { 10! }{ 2!2!3! }\)
[Because I comes 2 times, N comes 2 times and A comes 3 times]

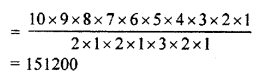
Hence, the total number of ways is 151200.

RBSE Solutions for Class 11 Maths