Rajasthan Board RBSE Class 11 Maths Chapter 7 Binomial Theorem Ex 7.1
Expand each expression in the following questions (Q. 1 to 5):
Question 1.
(2 – x)3
Solution :
(2 – x)3
= 3C0 ( 2 )3 + 3C1 ( 2 )2 (-x) + 3C2 ( 2 ) ( -x )2 + 3C3 ( -x )3
= 1 × 8 + 3 × 4x ( -x ) + 3 × 2 × x2 + 1 × ( -x )3
= 8 – 12x + 6x2 – x3
Question 2.
\({ \left( \frac { 2 }{ x } -\frac { x }{ 2 } \right) }^{ 5 }\)
Solution:
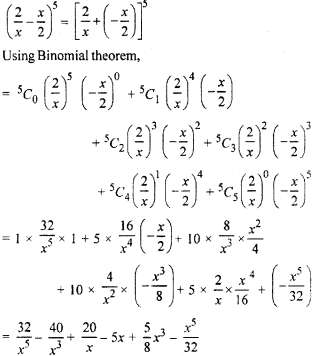
Question 3.
\({ \left( \frac { x }{ 3 } -\frac { 1 }{ x } \right) }^{ 6 }\)
Solution:
\({ \left( \frac { x }{ 3 } -\frac { 1 }{ x } \right) }^{ 6 }\),
By using Binomial theorem
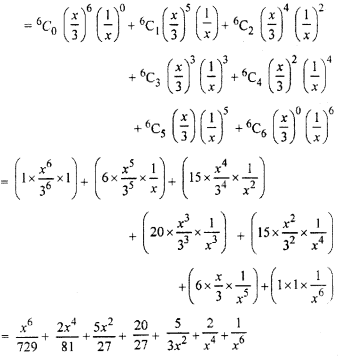
Question 4.
(3x + 2y)4
Solution:
(3x + 2y)4
By using Binomial theorem
= 4C0 ( 3x )4 ( 2y )0 + 4C1 ( 3x )3 (2 y ) + 4C2 ( 3x )2 ( 2y )2
+ 4C3 ( 3x ) ( 2y )3 + 4C4 ( 3x )0 ( 2y )4
= (1 × 34 × 1 × x4 × 1) + (4 × 33 × 2 × x3 y)+ (6 × 32 × 22 × x2 y2)
+ (4 × 3 × 23 × xy3)+ (1 × 1 × 24 × y4)
= 81x4 + 216x3y + 216x2y2 + 96 xy3 + 16 y4
Question 5.
\({ \left( \sqrt { \frac { x }{ a } } -\sqrt { \frac { a }{ x } } \right) }^{ 6 }\)
Solution:
\({ \left( \sqrt { \frac { x }{ a } } -\sqrt { \frac { a }{ x } } \right) }^{ 6 }\)
By using Binomial theorem
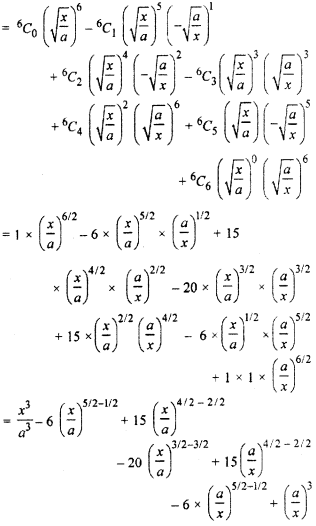
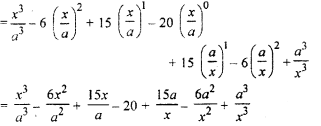
Using Binomial theorem find the values of following (Q. 6 to 9) :
Question 6.
(96)3
Solution :
(96)3
∵ 96 = 100-4
∴ (96)3 = (100 – 4)3 = [ 100 + (- 4)]3
By using Binomial theorem
963 = [100 + (- 4)]3
3C0 (100)3 ( – 4 )0 + 3C1 (100)2 (- 4)1
+ 3C2 (100) (- 4)2 + 3C3 (100)0 (- 4)3
= 1 x 1000000 x + 3 x 10000 x (-4)
+ 3 x 100 × 16 + 1 × 1 × (-64)
= 1000000 – 120000 + 4800 – 64
= 1004800 – 120064
= 884736 Hence, (96)3
= 884736
Question 7.
(101)4
Solution :
101 = 100 + 1
(101 )4 = (100 +1)4
By using Binomial theorem
(101)4 = (100 + 1)4
= 4C0 (100)4 (1)0 + 4C1 (100)3 (1)1
+ 4C2 (100)2 (1)2 + 4C3 (100) (1)3
+ 4C4 (100)0 (1)4
= 1 x 100000000 x 1 + 4 × 1000000 × 1 + 6
× 10000 x 1 + 4 x 100 × 1 + 1 x 1 x 1
= 100000000 + 4000000 + 60000 + 400+1
= 104060401
Hence, (101)4 = 104060401
Question 8.
(99)5
Solution :
99 = (100- 1)
995 = (100- 1)5 = [100+ (- 1)]5
By using Binomial theorem
995 = 5C0 (100)5 (-1)0 + 5C, (100)4 (-1)1
+ 5C2 (100)3 (- 1)2 + 5C3 (100)2 (- 1)3
+ 5C4 (100) (-1)4 + 5C5 (100)0 (-1)5
= 1 x 10000000000 x 1 + 5 x 100000000
× (- 1) + 10 x 1000000 × 1 + 10 × 10000
× (- 1)+ 5 x 100 × 1 + 1 × 1 × (-1)
= 10000000000 – 500000000 +
10000000 – 100000 + 500 – 1
= 10010000500 – 500100001
= 9509900499
Hence, (99)5 = 9509900499
Question 9.
(M)6
Solution :
(1.1)6 = (1 +0.1)6
= 6C0(1)6 (0.1)0 + 6C1 (1)5 (0.1)1
+ 6C2 (1)4 (0.1)2 + 6C3 (1)3 (0.3)3
+ 6C4 (1)2 (0.1)4 + 6C5 (1)1 (0.1)5 + 6C6 (1)0 (0.1)6
= (1 x 1 x 1) + (6 x 1 x 0-1) + {15 x 1 x (0.1)2}
+ {20 x 1 x (0.1)3} + {15 x 1 x (0.1)4}
+ {6 x 1 x (0.1)5} + {1 x 1 x (0.1)6}
= 1 + 6 x 0.1 + 15 x (0.1)2 + 20 x (0.1)3
+ 15 x (0.1)4+ 6 x (0.1)5 + (0.1)6
= 1 + 0.6 + 15 x 0.01 + 20 x 0.001 + 15 x 0.0001
+ 6 x 0.00001 +0.000001
= 1+0-6 + 0-15 + 0020 + 0-0015 + 0-00006 + 0000001
= 1-771561
Question 10.
Using Binomial theorem find which number is greater (M)100000 or 1000.
Solution :
(1.1)100000
= (1+0.1)1000000
= 10000C0 (1)10000 (0.1)0
+ 0000c1 (1)9999 (0.1)1 +……….
= 1 × 1 × 1 + 10000 × 1 × 0.1 +………
= 1 +1000 +… other positive numbers
= 1001+… other positive numbers
Hence(1.1)10000= 1001+… other positive numbers
But 1001>1000
Then (1.1)10000>1000.
(1.1)10000 is greater
Question 11.
Expand (a + b)4 – (a – b)4. Using this find the value of (√3 + √2)4 – (√3 – √2)4.
Solution :
By using binomial theorem,
(a + b)4 = 4C0 a4 b0 + 4C1 a3 b1
+ 4C2 a2 b2+ 4C3 ab3 + 4C4 a0 b4
= 4C0 a4 + 4C1 a3 b1 + 4C2 a2 b2
+ 4C3 ab3 + 4C4 b4 …. (1)
and (a – b)4 = 4C0 a4 (-b)0+ 4C1 a3 (-b)1
+ 4C2 a2 (-b)2 + 4C3 a1 (-b)3 + 4C4 a0 (-b)4
= 4C0 a4 – 4C1 a3 b + 4C2 a2 b2
– 4C3 ab4 + 4C4 b4 …. (2)
From equation (1) and (2) we have,
(a + b)4 – (a – b)4
= [4C0 a4 + 4C1 a3 b +4C2 a2 b2 + 4C3 ab3 + 4C4 b4]
– [4C0 a4 – 4C1 a3 b + 4C2 a2 b2 –4C3 ab3 + 4C4 b4]
= 4C0 a4 + 4C1 a3 b + 4C2 a2 b2 + 4C3 ab3 + 4C4 b4
– 4C0 a4 + 4C1 a3b – 4C2 a2b2 + 4C3 ab3 – 4C4 b4
= 2. 4C1 a3 b + 2. 4C3 ab3
= 2ab [4C1 a2 + 4C3 b2]
= 2ab [4a2 + 4b2] [∴ 4C1 = 4, 4C3 = 4]
= 2ab (a2 + b2)
Hence, (a + b)4 – (a – b)4 = 8ab (a2 + b2)
Now, putting a= √3 and b = √2
(√3 + √2)4 – (√3 – √2)4
= 8 √3 × √2 [(√3)2 + (√2)2]
= 8 √6 (3 + 2)
= 8 √6 × 5 – 40 √6
Hence (√3 + √2 )4 – (√3 – √2 )4 = 40 √6