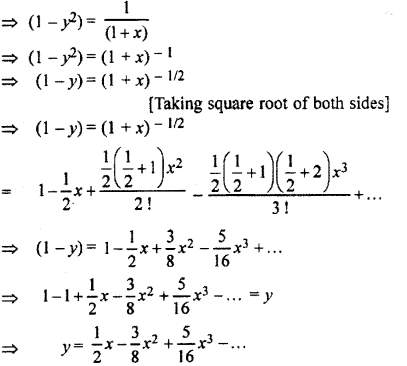RBSE Solutions for Class 11 Maths Chapter 7 Binomial Theorem Ex 7.4

Rajasthan Board RBSE Class 11 Maths Chapter 7 Binomial Theorem Ex 7.4

Question 1.
Expand the following Binomials upto fourth term:

Solution:
Expansion upto four terms of (1 + x²)^-2


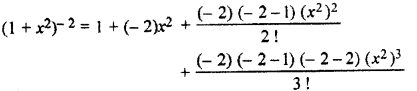
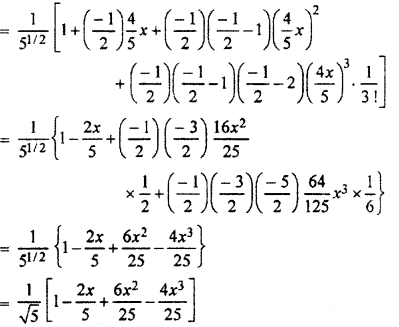
Question 2.
Find the required terms in the following expansions:
(i) Fourth term of (1 – 3x)^-1/3
(ii) Seventh term of (1 + x)^5/2
(iii) Eighth term of (1 + 2x)^-1/2
Solution:
(i) Fourth term of (1 – 3x)^-1/3
= Fourth term of (1 – 3x)^-1/3
= Fourth term of {1 + (- 3x)}^{– 1/3}

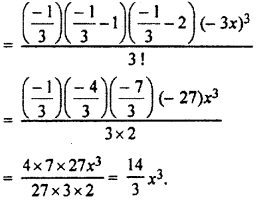
(ii) Seventh term of (1 + x)^5/2

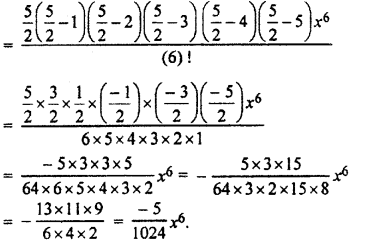
(iii) Eighth term of (1 + 2x)^-1/2

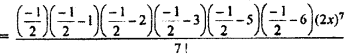
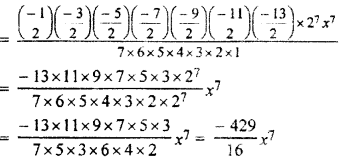
Question 3.
Find the general term of the following expansions:
(i) (a³ – x³)^2/3
(ii) (1 – 2x)^-3/2
(iii) (1 – x)^-p/q
Solution:
(i) General term in the expansion of (a³ – x³)^2/3

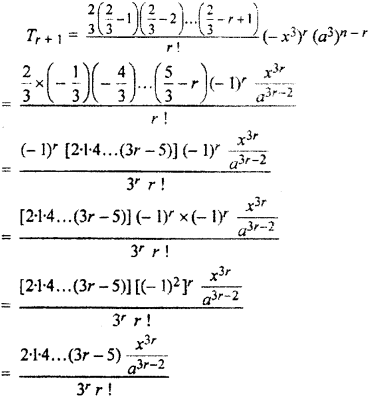
(ii) General term in the expansion of (1 – 2x)^-3/2

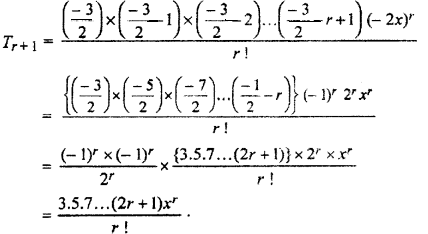
(iii) General term of in the expansion of (1 – x)^-p/q

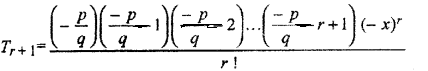
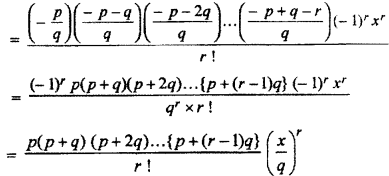
Question 4.
If x < 3, find the coefficient of (3 – x)^-8 in the expansion of (3 – x)^{– 5}.
Solution:
(x + 1)th term in the expansion of (3 – x)^-8

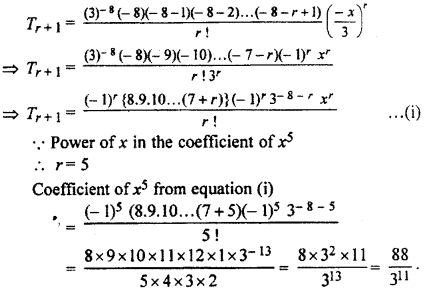
Question 5.
Find the coefficient of x⁶ in the expansion of (a + 2bx²)^-3
Solution :
(r + 1)th term in the expansion of (a + 2bx²)^-3

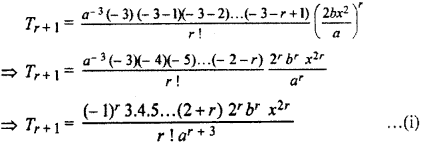
For the coefficient of x⁶ in the this term
2r = 6 ⇒ r = 3
Hence, from equation (i), coefficient of x⁶ in the expansion of (a + 2bx²)^-3

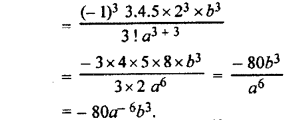
Question 6.
Find the coefficient of x¹⁰ in the expansion of

Solution:

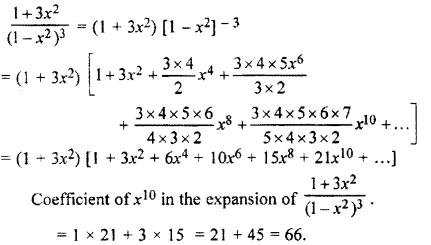
Question 7.
Find the coefficient of x^r in the expansion of (1 – 2x + 3x² – 4x³ + …)ⁿ and if x = \(\frac { 1 }{ 2 }\) and n = 1, then find the value of the expression.
Solution:
we know that (1 + x)^-2 = 1 – 2x + 3x² – 4x³ +…+ (-1)^r (r+1)x^r+ ….. (i)
Given progression (1 – 2x + 3x² – 4x³ +…)ⁿ
(1 – 2x + 3x² – 4x³ +…)ⁿ
= {(1 + x)^-2}ⁿ  [From equation (i)]
= (1 + x)^-2n

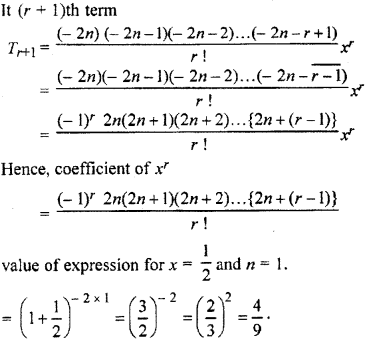
Question 8.
Prove that (1 + x + x² + x³ + …)² = 1 + 2x + 3x² + …
Solution:
We know that
1 + x + x² + x³ + … = (1 – x)^-1  …. (i)
(1 + x + x² + x³ + …)²
= {(1 – x)^-1}²  [From equation (i)]
= (1 – x)²

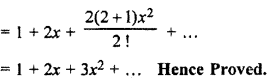
Question 9.
Prove that (1 + x + x² + x³ +….)  (1 + 3x + 6x²+ …)
= (1 + 2x + 3x² + …)²
Solution:
We know that
(1 – x)^-1 = 1 + x + x² + x³ +…           … (i)
and (1 – x)^-3 = 1 + 3x + 6x² + 10x³ + … (ii)
L.H.S. = (1 + x + x² + x³ +…)(1 + 3x + 6x² + …)
= {(1 – x)^-1} {(1 – x)^-3}
= {(1 – x)²}^-2
= {(1 – x)^-2}²
= (1 + 2x + 3x² +…)²
= R.H.S.
Hence Proved.

Question 10.
If x = 2y + 3y² + 4y³ + …then express y in series of as ascending powers of x.
Solution:
⇒ x = 2y + 3y² + 4y² + …
⇒ x = (1 + 2y + 3y² + 4y3 + …)- 1
[∵ (1 – x)^-2 = 1 + 2x + 3x² + …]
⇒ (x+ 1) = (1 -y)^-2

RBSE Solutions for Class 11 Maths