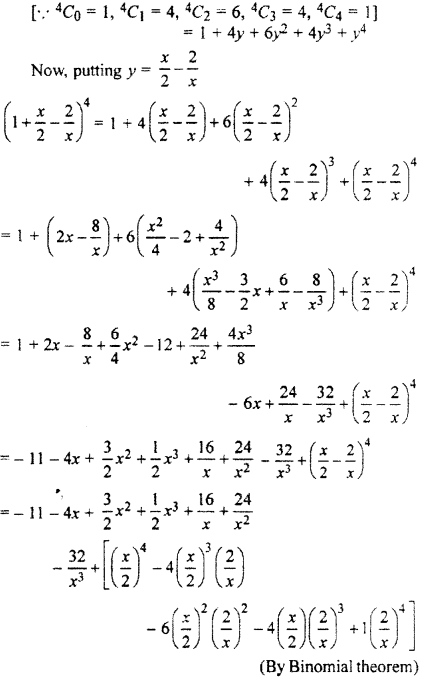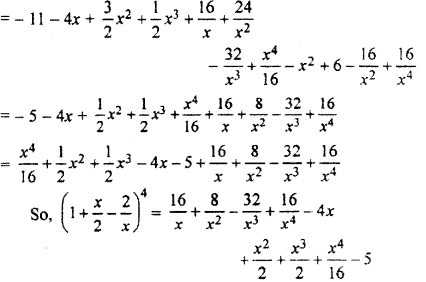Rajasthan Board RBSE Class 11 Maths Chapter 7 Binomial Theorem Miscellaneous Exercise
Question 1.
The number of terms in the expansion of
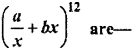
(A) 11
(B) 13
(C) 10
(D) 14
Solution :
Terms of R.H.S. of the expansion of (x + a)n is finite for the positive values of x and number of terms is (n + 1).
So, value of n is 12 in the given expression.
Hence, number of total terms = 12 + 1 = 13.
Hence, option (B) is correct.
Question 2.
The 7th term in the expansion of
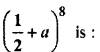
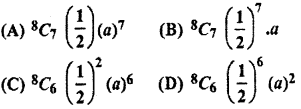
Solution :
7th term in the expansion of
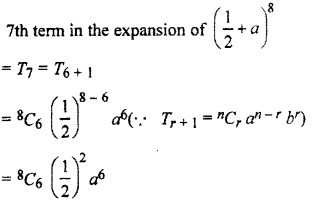
Hence, option (C) is correct.
Question 3.
The middle term in the expansion of (a – x)n is
(A) 56a3 x5
(B) -56a3 x5
(C) 70a4 x4
(D) -70a4 x4
Solution :
If n is even in (a + b)n, then its middle term

Question 4.
The constant term in the expansion
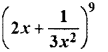
(A) 5th
(B) 4th
(C) 6th
(D) 7th
Solution :
(r + 1)th term in the expansion of
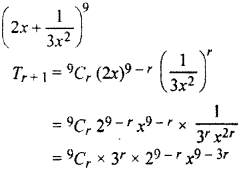
For constant term
x9 – 3r = x0
⇒ 9 – 3r=0
⇒ r = 3
Hence, r + 1 = 3 + 1 = 4th term is the constant term
Hence, option (B) is correct, Ans.
Question 5.
The general term in the expansion of (x + a)n
(A) nCr xn-r .ar
(B) nCr xr .ar
(C) nCn-r xn-r.ar
(D) nCn-r xr.an-r
Solution :
General term in the expansion of (x + a)n
⇒ Tr+1 = nCr xn-r ar
Hence, option (A) is correct.
Question 6.
The value of term independent of x in the expansion
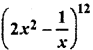
(A) 264
(B) -264
(C) 7920
(D) -7920
Solution :
(r + 1)th term in the expansion of

Question 7.
The coefficient of x-17 in the expansion of
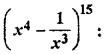
(A) 1365
(B) -1365
(C) 3003
(D) -3003
Solution :
(x + 1)th term in the expansion of

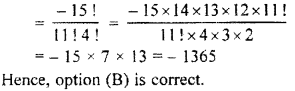
Question 8.
If in the expansion of (1 + x)18, coefficients of (2r + 4)th and (r – 2)th terms are equal then value of r is:
(A) 5
(B) 6
(C) 7
(D) 8
Solution :
In the expansion of (1 + x)18 coefficients of (2r + 4)th and (r – 2)th terms are 18C2r + 3 and 18Cr – 3 respectively
Given :
These are equal
Then, 18C2r + 3= 18Cr – 3
⇒ 2r + 3 = r – 3
or 2r+ 3= 18 -(r – 3)
For using the statement if
nCr = nCp or nCn-p
⇒ 2r – r = -3 – 3
or 2r + 3 = 18 – r + 3
⇒ r = -6 or r = 6
r is a natural number, so r = – 6 is not possible, then x = 6.
Hence, option (B) is correct. .
Question 9.
If in the expansion of (a + b)n and (a + b)n + 3 ratio of 2nd and 3rd, 3rd and 4th terms are equal, then value of n is :
(A) 5
(B) 6
(C) 3
(D) 4
Solution :
In the expansion of (a + b)n
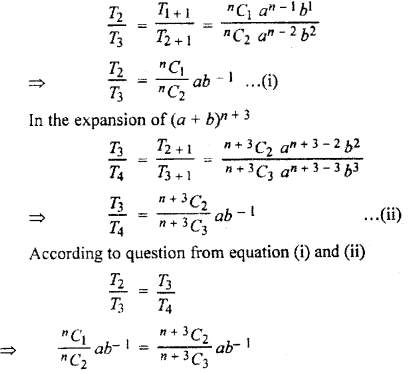
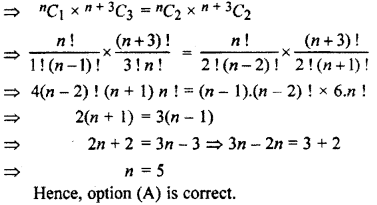
Hence, option (A) is correct.
Question 10.
If in the expansion of (1 + x)2n, coefficient of 3rd and (r + 2)th term are equal, then :
(A) n = 2r
(B) n = 2r – 1
(C) n = 2r + 1
(D) n = r + 1
Solution :
In the expansion of (1 + x)2n, 3rd term = 2nC3r – 1 and r + 2th term = 2nCr + 1
According to question,
2nC3r – 1 = 2nCr + 1
Now, 3r – 1 = r + 1 or 3r – 1 = 2n – r – 1
⇒ 3r – r – I + 1 or 3r + r = 2n – 1 + 1
⇒ 2r = 2 or 4r = 2n
⇒ r =1 or 2r = n
Hence, option (A) is correct.
Question 11.
Find the value of term independent of x in the expansion of (2x – 1/x)10 :
Solution :
(r + 1)th term of the expansion of (2x – 1/x)10
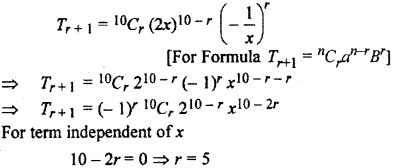
Hence, value of independent of x in the expansion of
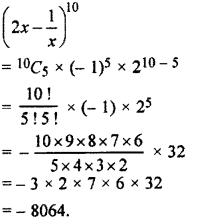
Question 12.
Find the number of term in the expansion of (x + a)200+ (x – a)200 after simplification.
Solution :
∵ (x + a)n + (x – a)n
= 2[nC0 xna0 + nC0 xn-2 – a2 + nC4xn-4 .a4 +…]
where n is an even number then
[Number of terms in the expansion of (x + a)n+ (x – a)n]
![]()
Here, n = 200
Hence, number of terms in the expansion
Will be
![]()
Hence, number of terms is 101 in the expansion.
Question 13.
If the expansion of (1 + x)n, C0 + C1 + C2 + C3 + … Cn are coefficients different terms then find the value C0 + C2 + C4… .
Solution :
(1 + x)n= nC0 1n + nC1 1n + nC1 1n-1 x1
nC2 1n-2 x2 + nC3 1n-3x3 +….
Putting x = 1
(1 + 1)n = nC0 + nC1 +nC2 + nC3 + ….
Putting x = – 1
(1 – 1)n = nC0 – nC1 +nC2 – nC3 + ….
Here nC0 + nC1 +nC2 + nC3 + …. = 2n … (i)
“C0 – “Ci + ”C2 – “C3 + … = 0 … (ii)
Adding equation (i) and (ii)
2[nC0 + nC2 + nC4 + …] = 2n
⇒ nC0 + nC2 + nC4 + … = 2n – 1
or C0 + C2 + C4 + … = 2n – 1
Question 14.
Find the value of
30C1 + 30C2 + 30C3 +… + 30C30 .
Solution :
(1 + x)n = nC0 + nC1x+nC2x2+ nC3x3+ ….
Putting x = 1
(1 + 1)n = nC0 + nC1 +nC2 + nC3 + …. + nCn
or 2n = nC0 + nC1 +nC2 + nC3 + …. + nCn
Here, putting n = 30.
230 = 1+ 30C1 +30C2 + 30C3 + …. + 30C3o
⇒ 1+ 30C1 +30C2 + 30C3 + …. + 30C3o = 230
⇒ 30C1 + 30C2 + 30C3 + … + 30c30 = 230 – 1
Question 15.
Find the middle term in the expansion of
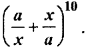
Solution :
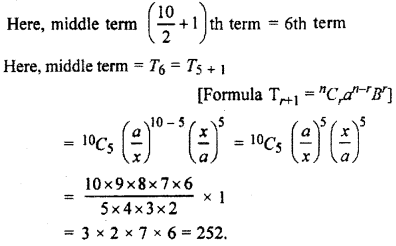
Question 16
In the product of expansion of (1 + 2x)6 (1 – x)7, find the coefficient of x5.
Solution :
Given expression
= (1 + 2x)6 (1 – x)7
∵ (1 + 2x)6 = 6C0 + 6C1 (2x)1 + 6C2 (2x)2
+ 6C3 (2x)3 + 6C4 (2x)4+ 6C5 (2x)5 + 6C6 (2x)6
= 1 + 6 × 2x + 15 × 4x2 + 20 × 8x3
+ 15 × 16x4+ 6 × 32 x 5+ 1 × 64x6
or (1 + 2x)6 = 1 + 12x + 60x2 + 160x3
+ 240x4+ 192x5 + 64x6 … (i)
[∵ 6C0 = 1, 6C1 = 6, 6C2 = 15, 6C3 = 20, 6C4 = 15, 6C5 = 6]
and (1 – x)7 = 7C0 – 7C1x + 7C2x2– 7C3x3 + 7C4x4 – 7C5x6 +,..
= 1 – 7x + 21x2 – 35x3+ 35x4-21x5 +….. (ii)
[7C0 = 1, 7C1= 7, 7C2 = 21, 7C3 = 35, 7C4= 35, 7C5 = 21]
Now (1 + 2x)6 (1 – x)7
= [1 + 12x + 60x2 + 160x3+ 240x4 + 192x4+ …]
= [1 – 7x + 21x2 – 35x3 + 35x4 – 21x5 + …]
Coefficient of x5 in the above expansion
[- 21 + 12 x 35 – 60 × 35 + 160 × 21+ 240 (-7) + 192 × 1]
= [- 21 + 420 – 2100 + 3360 – 1680 + 192]
= [-3801 + 3972]= 171.
Question 17.
If in the expansion of (1 + x)2n coefficient of 2nd, 3nd and 4th terms are in A.P. then prove that 2n2 – 9n + 7 = 0.
Solution :
In the expansion of (1 + x)2n, coefficient of 2nd, 3rd and 4th terms are
T2= T1 + 1= 2nC1
T3 = T2 + 1 = 2nC2
T4 = T3 +1 = 2nC3
According to questions,
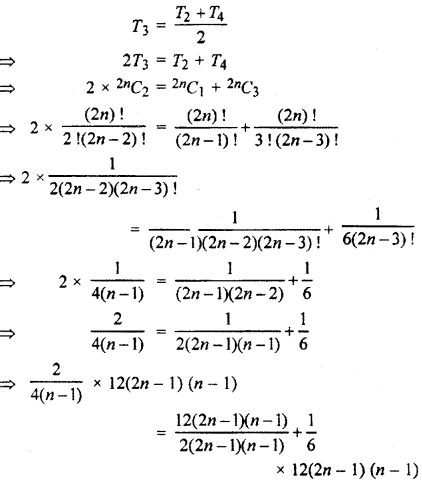
⇒ 6 (2n – 1) = 6 + 2(2n – 1) (n – 1)
⇒ 12n – 6 = 6 + 2(2n2 – 3n + 1)
⇒ 4 n2 – 6n + 2 – 12n + 6 + 6 = 0
⇒ 4n2 – 18n +14 = 0
⇒ 2n2 – 9n + 7 = 0.
Hence Proved.
Question 18.
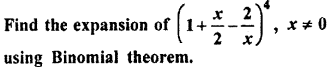
Solution :