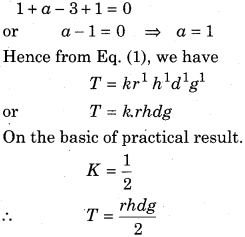RBSE Solutions for Class 11 Physics Chapter 1 Physical World and Measurement

Rajasthan Board RBSE Class 11 Physics Chapter 1 Physical World and Measurement

RBSE Class 11 Physics Chapter 1 Textbook Exercises with Solutions

RBSE Class 11 Physics Chapter 1 Very Short Answer Type Questions

Question 1.
What is the unit of luminous intensity in S.I. system?
Answer:
S.I. unit of luminous intensity is candela (cd).

Question 2.
What is the unit of amount of a substance?
Answer:
The unit of amount of substance is mole.

Question 3.
1 J is how much of ergs?
Answer:
1 J = 10⁷ ergs.
Question 4.
What is the unit of Planck’s constant?
Answer:
Joule × second

Question 5.
How many significant figures are there in 0.005?
Answer:
One (1)

Question 6.
How many base and supplementary’ units are there in S.I. system?
Answer:
Base or fundamental units = 7 supplementary units = 2.

Question 7.
Write the dimensional formula for Boltzmann constant?
Answer:
[M¹L²T^-2K^-1]

Question 8.
How many types of errors are there?
Answer:
Three types

Question 9.
What is the dimensional formula of surface tension?
Answer:
[M¹L⁰T^-2]

Question 10.
What is the wavelength of Kr⁸⁶ in 1 m?
Answer:
1650763.73

Question 11.
Name the physical quantity it’s dimensional formula is same as that of impules.
Answer:
Momentum.

Question 12.
Name two dimensionless physical quantities.
Answer:
Angle, Refractive index

Question 13.
How much is the percentage error in constant K?
Answer:
Zero

Question 14.
If Ax is the error in measurement of a physical quantity x, then how much is the percentage error in xm?
Answer:
\(m \frac{\Delta x}{x} \times 100 \%\)

Question 15.
If the units of each force and length is doubled, then how much times would be the unit of energy?
Answer:
4 times

RBSE Class 11 Physics Chapter 1 Short Answer Type Questions

Question 1.
What is Science?
Answer:
The word “Science” originates from the latin verb “Scientia” which means “to know”. Science can be said to be as old as human species. Science can be defined as below.

“The knowledge gained through observations and experiments, when organised systematically, is called science”.

Question 2.
What is a unit? How many systems are there for units?
Answer:
Unit : “Unit is a standard quantity of the same kind with which a physical quantity is compared for its measurement.” In the process to know or express the magnitude of a physical qunatity ‘Q terms of :
(i) Size of unit (u) used.
(ii) The numerical value of the unit. So, Q = nu

If the size of the unit is changed then the value of n will also change for the same amount of physical quantity Question, Therefore.
\(Q=n_{1} u_{1}=n_{2} u_{2}=n_{3} u_{3}=\dots\)
⇒ nu = Constant

1. C.G.S. System: It is a French system of units. In this system, length is measured in centimeters (cm), mass is measured in grams (g) and time is measured in seconds (s).
2. M.K.S. System: It is also a French system of units. In this system, length is measured in meters (m), mass in kilograms (kg) and time in seconds (s).
3. F.P.S. System: It is a British system of units. In this system the length is measured is foot (l), mass in pounds (p) and time in seconds (s).

Question 3.
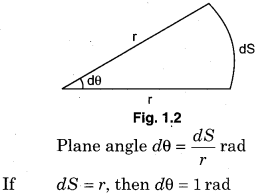
Define a radian.
Answer:
Radian : The plane angle is given by
\(\begin{aligned} d \theta &=\frac{d s}{r} \mathrm{rad} \\ \text { If } & d s=r, \text { then } d \theta=1 \mathrm{rad} \end{aligned}\)
Thus, “One radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle.”

Question 4.
Write the quantities of a S.I. system of units.
Answer:
Quantities of S.I. system of units :
The French name of this system is “Le System International d Units”. It is abbreviated as S.I. system. It has seven fundamental (or basic) units and two supplementary units.

Fundamental quantities: Length, mass, time, electric current, temperature, luminous intensity and amount of substance.
Supplementary quantities : Plane angle, and solid angle.

Question 5.
Write the advantages of dimensional, analysis.
Answer:
There are following uses or advantages of dimensional analysis.

1. To check the correctness of a given relation.
2. To derive the relationship between various physical quantities.
3. To determine the dimensions of unknown quantities.
4. Conversion of one system of units into the other system of units.

Question 6.
Is it possible to have dimensionless and unitless physical quantities?
Answer:
Yes, there are many such quantities which have no dimension as well as no unit. For example.

1. A strain is dimensionless and unitless.
2. Angle and solid angle also belong to this category.

RBSE Class 11 Physics Chapter 1 Long Answer Type Questions

Question 1.
Explain the International System of Units and define the different fundamental units.
Answer:
The international system of units (S.l. system of units) The international system of units (abbreviated as SI, from the French system international (d’ unites) is the modern form of the metric system and is the most widely used system of measurement.

The SI is based on the following seven fundamental units and two supplementary units as listed in the table.

Fundamental quantities and their units

s. No.	Name of a physical quantity	Symbol of quantity	SI unit	Symbol of unit
1.	Length	L	Meter	M
2.	Mass	M	Kilogram	Kg
3.	Time	T or T	Second	S
4.	Temperature	T or θ	Kelvin	K
5.	Current	I	Ampere	A
6.	Amount substance	N	Mole	Mol
7.	Intensity light (Luminous intensity)	Iv	Candela	Cd

Supplementary quantities and their units

S. No	Supplementary physical quantity	Unit	Symbol used
1.	Plane angle	Radian	Rad
2.	Solid angle	Steradian	Sr

The above seven basic and two supplementary units are found to be sufficient to obtain the units of physical quantities from all branches of physics.

(ii) In addition to the fundamental units and the supplementary units, there are a large number of derived units on this system. Some of the derived units are listed in table.

Supplementary Units: Definitions
1. Radian: One radian is the angle subtended at the centre of a circle by an arc equal in length to the radius of the circle.

2. Steradian: One steradian is the solid angle subtended at the centre of a sphere, by that surface which is equal in area to the square of the radius of the sphere.

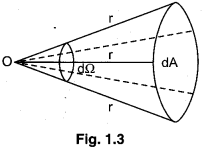
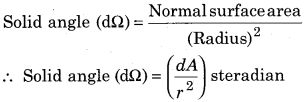
If dA = r² then dΩ = 1 steradian In case of complete surface area, the cubic angle subtended by it

\(\Omega=\frac{4 \pi r^{2}}{r^{2}}=4 \pi\) steradian

Question 2.
Differentiate fundamental units and derived units by giving examples. Write popular units.
Answer:
Physical quantities are of two types:
(i) Fundamental quantities Fundamental units are those units, which can neither be derived from one another nor can they be further resolved into any other units. The quantities mass, length and time are called fundamental physical quantities and their units are known as

fundamental units because:
(i) Mass, length and time cannot be obtained from one another.
(ii) All other physical quantities in mechanics can be obtained from them.
(iii) Derived quantities: The units of all such physical quantities, which can be expressed in terms of the fundamental units of mass, length and time are called derived units. For example force, work, power, energy, pressure, momentum, acceleration, density, etc. are all derived units and they can be obtained by writing their defining equations in terms of fundamental physical quantities. To explain, let us consider the defining equation of speed, we know that:

An international system of units (Si. system of units)
The international system of units (abbreviated as SI, from the French system international (d’ unites) is the modern form of the metric system and is the most widely used system of measurement. The SI is based on the following seven fundamental units and two supplementary units as listed in the table.

Question 3.
Derive the relation for the conversion of one unit system to another using the dimensions.
Answer:
1. Conversion of units of physical quantities from one system to another system: The method of dimensional analysis can be used to obtain the value of the physical quantity in some other system when its value in one system is given.
As discussed earlier, the measurement of a physical quantity is given by:
Q = nu
If the unit of a physical quantity in a system is u₁, and the numerical value is n₁, then:
Q=n₁u₁ …………….(1)
Similar in the other system if the unit is u2 and magnitude is n2 then:
Q= n₂u₂ …………………..(2)
From Eqs. (1) and (2)
n₁u₁ = n₂u₂ ……………..(3)
If a,b,c are the dimensions of a physical quantity in mass, length and time, then:
\(n_{1}\left[\mathrm{M}_{1}^{a} \mathrm{L}_{1}^{b} \mathrm{T}_{1}^{c}\right]=n_{2}\left[\mathrm{M}_{2}^{a} \mathrm{L}_{2}^{b} \mathrm{T}_{2}^{c}\right]\)
Here M₁ ,L₁ ,T₁ and M₂ ,L₂ ,T₂ are the units of mass, length and time in the two systems, then
\(n_{2}=n_{1}\left[\frac{\mathrm{M}_{1}}{\mathrm{M}_{2}}\right]^{a}\left[\frac{\mathrm{L}_{1}}{\mathrm{L}_{2}}\right]^{b}\left[\frac{\mathrm{T}_{1}}{\mathrm{T}_{2}}\right]^{c}\)

The equation can be used to find out the value of a physical quantity in the second or the new system, when its value in first system is known.

Question 5.
What is meant by errors of measurement? How do errors vary with a combination of errors? Explain.
Answer:
Accuracy and Errors in Measurement The measuring process is essentially a process of comparison. To measure any physical quantity, we compare it with a standard (unit) of that quantity. No measurement is perfect as the errors involved in the process cannot be removed completely. Hence, in spite of our best effort, the measured value of a quantity is always somewhat different from its actual value, or true value.

Measurement error:
The measurement error is defined as the difference between the true or the actual value and the measured value

i.e., error is quantity = (True value — measurement value) of the quantity.

Absolute Error, Relative Error and Percentage Error.
1. Absolute error: Absolute error in the measurement of a physical quantity is the magnitude of the difference between the true value and the measured value of the quantity.

Let a physical quantity can be measured n times. Let the measured vahie be a₁,a₂,a₃ a the arithmetic mean of these values is:
\(a_{m}=\frac{a_{1}+a_{2}+a_{3} \dots a_{n}}{n}\)

Usually, a_m is taken as the true value of the quantity, if the same is unknown otherwise by definition, absolute errors in the measured value of the quantity are
\(\begin{aligned} \Delta a_{1} &=a_{m}-a_{1} \\ \Delta a_{2} &=a_{m}-a_{2} \\ \vdots & \\ \Delta a_{n} &=a_{m}-a_{n} \end{aligned}\)

Absolute errors may be positive in certain cases and negative in the other cases.

2. Mean absolute error: It is the arithmetic mean of the magnitude of absolute errors in all the measurements of the quantity it is represented by tã. Thus,

Hence the final result of the measurement may be written as \(a=a_{m} \pm \Delta \overline{a}\)

This implies that any measurement of the quantity is likely to lie between \(\left(\alpha_{m}+\Delta \overline{a}\right)\) and \(\left(a_{m}-\Delta \overline{a}\right)\)

3. Relative error: The relative error or fractional error of measurement is defined as the ratio of mean absolute error to the mean or value of the quantity measured. Thus,

4. Percentage error: When the relative/fractional error is expressed in term of percentage, we call it a percentage error. Thus,
percentage error \(=\frac{\Delta \overline{a}}{a_{m}} \times 100 \%\)

Question 6.
What are the rules to determine the significant figures? Explain each rule by giving examples.
Answer:
Significant Figures
The significant figures express the accuracy with which the physical quantity may be expressed. They are the digits which give us useful information about the accuracy of the measurement.

Greater the number of significant figures obtained when making a measurement, more accurate is the measurement, conversly, a measurement made to only few significant figure is not a very accurate one. For example, a recorded figure of 5.32 means the quantity can be relied on as accurate to three significant figures and a figure of 5.32 1 is said to be accurate to four significant number.

The following rules have been set up for determining the number of significant figures:
1. All non-zero digits are significant. 243,48 contains five significant figures.
2. All zeros occuring between two nonzero digits are significant. For example, 46.0009 contains six significant figures.
3. All zeros to the right of a decimal point and to the left of a non-zero digit are never significant 0.00678 contains three significant figures. The single zero conventionally placed to the left of the decimal point in such an expression is also never significant.
4.
(a) All zeros to the right of a decimal point are significant if they are not followed by a non-zero digit. For example, 30.00 contains four significant figures.
(b) All zeros to the right of the last non-zero digit after the decimal point are significant. For Example, 0.054300 contains five significant figures.

5.
(a) All zeros to the right of the last (rightmost) non-zero digit are not significant.
Ex. 3030 contains three significant figures.
(b) All zeros to the right of the last non-zero digit are significant if they come from a measurement. Suppose that the distance between two objects is measured to be 3030 m. Then 3030 m contains four significant figures.
6. Change of units does not change the number of significant figures in a measurement.

For example, the length x = 2.308 cm ha four significant digits. In different units, the same length can be written as x = 23.08 mm: x = 0.00002308 km. All these numbers have the same number of significant figures namely four, the digits 2, 3, 0 and 8.

Question 7.
What are the rules for rounding off the numbers? Explain each rule with suitable examples.
Answer:
Rounding Off the Digits
Rounding off a number is done to obtain its value with a definite number of significant figures. For this following are the rules:

1. 1f the digit to drop is less than 5, then the preceding digit is not changed.
   For e.g., 1.24 is rounded off to 1.2.
2. If the digit to drop is greater than 5. than the preceding digit is raised by 1.
   For e.g., 19.48 is rounded off to 19.5.
3. If the digit to drop is 5 and the preceding digit is even, then it is not changed.
   For e.g., 1.25 is rounded off to 1.2.
4. If the digit to drop is 5 and the preceding digit is odd, then it is increased by 1.
   For e.g., 3.35 is rounded off to 3.4.

Example 18. Let’s round off 92.810576 to:

(a)	1 significant figure	9 is the first non-zero digit, that means the first significant figure. In 92.810576 the second figure is 2 which is less than 5 so we round down the number to 90
(b)	3 significant figures	In 92.810576, 928 are the first three digits, the next figure is 1 which is less than 5, so we round down given number to 3 sig. fig. = 92.8.
(c)	6 significant figures	In 92.810576, the first six significant numbers are 92.8105. The zeros between the figures are significant. The next figure 7 which is more than 5, so we round up number as = 92.8106

Example 19. Let’s round off 0.0046753 to:

(a)	1 significant figure	figures in their correct places. In the above number the figure to the right of 4, is 6 which is more than 5, so we round up the number. When we round off 0.0046753 to 1   sig figures is = 0.005
(b)	2 significant figures	When we round off 0.0046753 to 2 significant figure is 0.0047.
(c)	4 significant figures	In the above number, 5 is the 4th significant figure. The figure to the right of 5 is 3 which is less than 5, so we round down the number. When we round off this number

Question 8.
How is the correctness of a formula or a relation is checked using the dimensional equations? Explain with examples.
Answer:

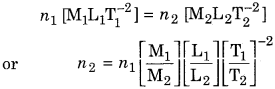
Both newton and dyne are units of force. The dimensional formula of force.
\([\mathrm{F}]=\left[\mathrm{M}^{1} \mathrm{L}^{1} \mathrm{T}^{-2}\right]\)
This dimensional formula is compare by the relation \(\left[\mathrm{M}^{a} \mathrm{L}^{b} \mathrm{T}^{c}\right]\)

Question 9.
Write an essay on the importance of Physics.
Answer:
We are surrounded by physics all the time, and whether we realize it or not, we use physics everyday. Physics the study of matter and energy, is an ancient and broad field of science.

The word ‘Physics’ comes from the Greek word ‘Fusis’ meaning ‘Knowledge of nature’ and in general, the field aims to analyze and understand the natural phenomena of the universe.

Though, there are many definitions of physics, yet it can be defined as, “The study of the properties of matter, energy and their mutual relationship.

Scope and Expansion of Physics
Physics is the branch of science, which deals with the properties of matter and energy and the relationship between them. It also tries to explain the material world and the natural phenomena of the – universe. The scope of physics is very wide and vast. It deals with not only the tinniest particle of atoms but it also dwells upon the natural phenomenon like galaxy, milky way, solar and lunar eclipse etc.

Branches of Physics
Physics is broadly classified into two parts.
(A) Classical physics
(B) Modern physics.

For your information

1. Macroscopic physics: Under the macroscopic, physics comes the astronomical and earth related incidents. The principles of classical mechanics clearly define macroscopic physics.
2. Microscopic physics: Microscopic physics covers the molecular, atomic and nuclear incidents. Quantum mechanics is studied to understand the microscopic physics.
3. Mesocopic physics: It is a subdiscipline of condensed matter physics that deals with materials of an intermediate length. The scale of these materials can be describeed as being between the size of a quantity of atoms (such as a molecule) and of materials measuring micrometers.

(A) Classical physics: Classical physics includes the traditional branches and topics that were recognized and fairly well developed before beginning of the 20th centuary. It is mainly concerned with the laws of motion and gravitation by Sir Isaac Newton and a kinetic theory and thermodynamic by James Clark Maxwell. Classical physics is mainly concerned with matter and energy. In this branch, energy and matter are considered as separate entities.

Classical mechanics, Optics, Acoustics and Electromagnetics are the traditional branches of classical physics.
(i) Mechanics: Mechanics is the study of physics of motion and how it relates to the applied forces. It lays the foundation of understanding the world around us through the question of how and why a thing moves.

(ii) Thermodynamics: Thermodynamics is the branch of physics, which deals with the study of heat and its relation with energy and work. This branch also deals with the study of gaseous systems. The change in temperature, internal energy and entropy of the system through external work are investigated. Modes of transfer of heat, efficiency of heat engines and refrigerators are also included in thermodynamics.

(iii) Electromagnetism: Electromagnetism is a branch of physics involving the study of electricity, magnetic effect and electromagnetic waves i. e., it deals with the study of the electromagnetic force, a type of physical interaction that occurs between electrically charged particles. The electromagnetic force usually exhibits electromagnetic field such as the electric field, the magnetic field and light.

(iv) Acoustics: The word acoustics has been derived from a Greek word ‘akouen’, meaning ‘to hear’. Hence we can define acoustics as a branch of physics, which studies how sound is produced, transmitted, received and controlled. It also deals with the effects of sounds in various mediums t.e, gases, liquids and solids.

(v) Optics: Optics involves the study of various phenomena connected with light and optical instruments like microscope, telescope etc. The topics studied in optics include images formed by lenses and mirrors, reflection, refraction, interference, diffraction, dispersion and polarization of light.

(B) Modern physics: Modern physics is the branch of physics, which is mainly concerned with the theory of relativity and quantum mechanics.

Albert Einstein and Max Plank were the pioneers of modern physics.

1. Relativity: Relativity is concerned with the study of those bodies that move with the speed almost same as the speed of light.
2. Quantum Mechanics: In quantum mechanics, we study the about modern principles of physics, dual nature of light and particles etc.
3. Atomic Physics: Atomic physics is the branch of physics which deals with the composition of atom apart from nucleus. It is mainly concerned with the arrangement and behaviour of electrons in shells around the nucleus.
4. Nuclear Physics: Nuclear physics is the branch of physics which deals with constituents, structure, behaviour and interaction of atomic nuclei. In the modern age, nuclear physics has got a very wide scope. It is used in power generation, nuclear weapons, medicines etc.

Apart from these branches, there are many branches of physics. Some of them are… Bio Physics, Electronics, Plasma-Physics, High Energy Physics, Astrophysics, Condensed Matter Physics, Solid State Physics, Environmental Physics, Computational Physics, Polymer Physics, Materials Physics and Cryogenics.

Question 10.
Explain the parallax method for measuring large distances. With the help of it, explain the method to determine the shape of a heavenly body.
Answer:
Measurement of Large Distances
Length: It is defined as the difference between two positions taken by two events that occur instantly.

(i) Parallax Method: When an object is seen by closing our right and left eye alternatively, there is a shift in the position of the object w.r.t. the background observed. This is known as parallax.

Imagine an object P placed at a distance x from our eyes. Let the line joining the object to left and right eye make O angle w.r.t. each other. O is called parallax angle.

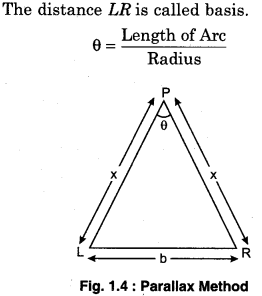
(ii) Size of Astronomical Object: Diameter of Moon: Let Moon be the astronomical object whose diameter is to he measured. We observed Moon with the help of a telescope. Let it be observed from a place F on Earth and make an angle O with the two ends P and Q of moon and the point K, as shown in fig. 1.5. O is called the angular diameter of the Moon.

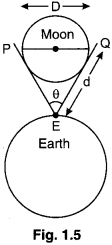
• Lt d be the distance of the Moon from the Earth.

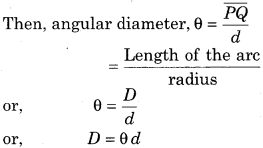
(iii) Reflection or Echo Method: A gun is fired towards the hill and the time taken between instant of firing and hearing of echo bet. In this time interval, sound first travels towards the hill from the place of firing and then hack from the hill to the place of firing. Lt u be the speed of sound. x be the distance of hill from the place of firing the gun, then
\(2 x=v \times t \quad \text { or } \quad x=\frac{v t}{2}\)

Ex: The time taken by a laser beam to reach the moon from the earth and reflect back ¡s 2.56 s. Calculate the distance of the Moon from the Earth.
Solution :
Given; t = 2.56 s
speed of light;
\(v=c=3 \times 10^{8} \mathrm{m} / \mathrm{s} ; d=?\)

Example 10 : The distance of the sun from earth is 1.496×10” m. If the angular diameter of the sun is 1920”. Find out the diameter of the sun.
Solution :
Given the distance to the sun from the
earthd=1.496×1011 m Sun
Angular diameter of the sun

RBSE Class 11 Physics Chapter 1 Numerical Problems

Question l.
The velocity of a body is v = A + Bt, then what are the dimensions of A and B ?
Solution:
The velocity of a body
11 = A + Bt
On applying the principle of homogeneity, The dimensional formula of A = Dimensions of v.
\(=\left[\mathbf{M}^{0} \mathbf{L}^{1} \mathbf{T}^{-1} \mathbf{1}\right.\)
Similarly, the dimensions of Bt = Dimensions of v
∴ Dimensions of B = dimensions of \(\frac{v}{t}\)
\(\begin{array}{l}{=\frac{\left[\mathrm{L}^{1} \mathrm{T}^{-1}\right]}{\left[\mathrm{T}^{1}\right]}=\left[\mathrm{L}^{1} \mathrm{T}^{-2}\right]} \\ {=\left[\mathrm{M}^{0} \mathbf{L}^{1} \mathbf{T}^{-2}\right]}\end{array}\)

Question 2.
In relation, F = a + bx, where F is the force, x is the distance. Calculate the dimensions of a and b.
Solution:
Given relation,
F = a + bx
Applying the principle of homogeneity of dimensions. We have,
Dimensions of a = dimensions of F
\(=\left[\mathbf{M}^{1} \mathbf{L}^{1} \mathbf{T}^{-2} \mathbf{1}\right.\)
Dimension of bx = dimensions of F
Dimensions of b = dimensions of \(\frac{F}{x}\)
\(\begin{aligned} &=\frac{\left[\mathrm{M}^{1} \mathrm{L}^{1} \mathrm{T}^{-2}\right]}{\left[\mathrm{L}^{1}\right]} \\ &=\left[\mathrm{M}^{1} \mathbf{L}^{0} \mathbf{T}^{-2}\right] \end{aligned}\)

Question 3.
In the gas equation, \(\left(\boldsymbol{P}+\frac{\boldsymbol{a}}{\boldsymbol{V}^{2}}\right)(\boldsymbol{V}-\boldsymbol{b})=\boldsymbol{R} \boldsymbol{T}\), where P is pressure, V is volume, R is gas constant and T is temperature. Calculate the dimensional formula of a and b.
Solution:
Given equation is,
\(\left(\boldsymbol{P}+\frac{\boldsymbol{a}}{\boldsymbol{V}^{2}}\right)(\boldsymbol{V}-\boldsymbol{b})=\boldsymbol{R} \boldsymbol{T}\)
Applying principle of homogeneity,
Dimensional formula of \(\frac{a}{V^{2}}=\) Dimensional formula of P
∴ Dimensional formula of a = Dimensional formula of \(P . V^{2}\)
\(\begin{array}{l}{=\left[\mathbf{M}^{1} \mathbf{L}^{-1} \mathbf{T}^{-2} \cdot \mathbf{L}^{6}\right]} \\ {=\left[\mathbf{M}^{1} \mathbf{L}^{5} \mathbf{T}^{-2}\right]}\end{array}\)
Similarly dimensional formula Dimensional formula of V
\(=\left[\mathbf{M}^{0} \mathbf{L}^{3} \mathbf{T}^{0}\right]\)

Question 4.
If the value of universal gravitational constant G is 6.67 x 10^-11 N m^-2/kg² in M.K.S. system, then determine its value in C.G.S. system using the dimensions.
Solution:
Given : G = 6.67 x 10^-11 N m^-2/kg²
To determine the value of G is (G.S. system formula used)

Question 5.
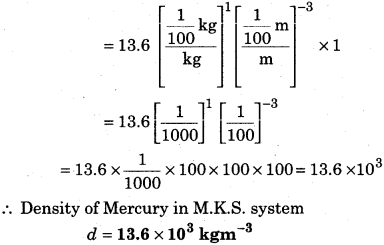
The density of Mercury is 13.6 g .cm^-3. Calculate its value in M.K.S. system using the dimensions.
Solution:
Given density d = 13.6 g.cm^-3
To determine its value in M.K.S. unit.
Formula used,
\(n_{2}=n_{1}\left[\frac{\mathbf{M}_{1}}{\mathbf{M}_{2}}\right]^{a}\left[\frac{\mathbf{L}_{1}}{\mathrm{L}_{2}}\right]^{b}\left[\frac{\mathbf{T}_{1}}{\mathbf{T}_{2}}\right]^{c}\)
The dimensional formula of density = [M¹L^-3T⁰]

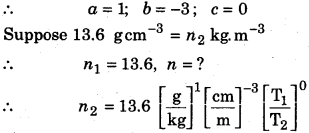
Question 6.
Check the correctness of the relation: \(\mathbf{Y}=\frac{M g L}{\pi r^{2} l}\) using the dimensional analysis.
Solution:
The given relation,
\(\mathbf{Y}=\frac{M g L}{\pi r^{2} l}\) ………………………(1)
Dimensional formula of L.H.S.= [M¹L^-1T^-2]
and dimensional formula of R.H.S.

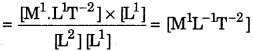
Since the dimensions of both the sides are the same, therefore the given relation (1) is “correct”.

Question 7.
To check the correctness of the relation \(: \frac{1}{2} m v=m g h\) using the dimensional analysis.
Solution:
The given relation,
\(\frac{1}{2} m v=m g h\) …………………..(1)
The dimensional formula of L.H.S.
\(=\left[\mathbf{M}^{1} \mathrm{L}^{1} \mathrm{T}^{-1}\right]\)
and the dimensional formula of R.H.S.
\(\begin{array}{l}{=\left[\mathrm{M}^{1} \cdot \mathrm{L}^{1} \mathrm{T}^{-2}\right] \mathbb{L}^{1} \mathrm{J}} \\ {=\left[\mathrm{M}^{1} \mathrm{L}^{2} \mathrm{T}^{-2}\right]}\end{array}\)
Since the dimension of both the sides are not equal, therefore given relation is “incorrect”.

Question 8.
In a test-tube, there is a liquid filled with surface tension T. The surface tension of the liquid depends upon the radius of the test-tube (r), height of the liquid column in tube (h), density of the liquid filled (d) and the acceleration due to gravity (g). Establish a relation for surface tension using the method of dimensions.
Solution:
In the Question dependence of T is given on four quantities. But using dimension analysis we can determine the value of dimensions of three unknown quantities only. Therefore, we will consider one quantity independent. For our purpose, we are considering r as constant. Now applying the given dependence, we have,

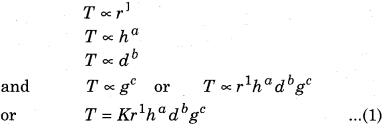
The dimensional formula of L.H.S.
\(=\left[\mathrm{M}^{1} \mathrm{L}^{0} \mathrm{T}^{-2}\right]\)
The dimension of a formula of R.H.S.

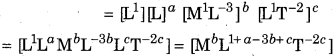
Since, for the correctness of formula (1), the dimensions of both the sides should be equal.
Therefore, on comparing the dimensions of both the sides, we have,

Substituting the values of b and cis EQuestion (3), we
get,

RBSE Solutions for Class 11 Physics