Rajasthan Board RBSE Class 11 Physics Chapter 10 Properties of Material Substances
Class 11 Physics Chapter 10 Textbook Exercises With Solutions
Class 11 Physics Chapter 10 Very Short Answer Type Questions
Question 1.
What is the force called by applying which the body changes its shape and size?
Answer:
The force that changes the shape and size of the body is called the Deforming force.
Question 2.
What is the property called by which the body regains its original shape and size after the removal of deforming force.
Answer:
Elasticity is the property due to which the body regains its original shape and size after the removal of deforming force.
Question 3.
What is the unit of stress?
Answer:
∵ Stress = \(\frac { F }{ A } \)
![]()
Question 4.
Write the dimension formula of strain.
Answer:
Strain is the ratio of same physical quantities of same dimension hence it is dimensionless.
∴ Dimension of strain = [M0L0T0]
Question 5.
Write down the modulus of elasticity of copper, steel, glass and rubber in ascending order.
Answet:
Rubber, Glass, Copper, Steel.
Question 6.
What is the. ratio of stress to strain called within the limit of elasticity?
Answer:
The ratio of stress to strain for any given material is called modulus of elasticity.
Question 7.
What is the unit of modulus of elasticity?
Answer:
∵ Modulus of elasticity = \(\frac { Stress }{ Strain } \)
Since, strain is a dimensionless quantity
∴ Unit of modulus of elasticity is same as that of stress i.e., Nm-2
Question 8.
What is the ratio of lateral strain to longitudinal strain called?
Answer:
The ratio of lateral strain to longitudinal strain is called Poisson’s ratio.
Question 9.
Is stress a vector quantity?
Answer:
No, stress is not a vector quantity.
Question 10.
Will the potential energy increase or decrease in pressing a solid or stretching a wire?
Answer:
The potential energy will increase in both the situations.
Question 11.
When we stretch a wire, why do we have to do work?
Answer:
When a wire is stretched, the internal reactive force comes in to play which opposes this action. Hence to overcome this opposing force, work is done. This work is stored in the form of elastic energy in the wire.
Question 12.
What is the dimensional formula of modulus of rigidity?
Answer:
Dimensional formula- of modulus of rigidity is M1 L-1 T-2.
Class 11 Physics Chapter 10 Short Answer Type Questions
Question 1.
What do you understand by elasticity?
Answer:
“Elasticity is the ability of a body to resist the change in shape or size caused by a deforming force and to return to its original size and shape when the deforming force is removed.” Those bodies which regain its original configuration immediately and completely after the removal of deforming force are called perfectly elastic bodies. And those bodies which does not regain its original configuration at all on the removal of deforming force are called perfectly plastic bodies.
Question 2.
What are resitution forces?
Answer:
A substance is in equilibrium position in the original form due to the effect of interatomic force. When external force is applied on any substance then as a result there is change in the shape or size or both of the substance and the internal reactive force is produced in the substance. When external forces are removed then due to internal reactive forces, the substance regains its original configuration. These interrial reactive forces are called restoring or resitution force.
Question 3.
What is stress?
Answer:
A substance is in equilibrium position in its original form due to the effect of interatomic forces. When external force is applied on any substance then as a result there is change in the shape or size or both of the substance and internal reactive force is produced in the substance. When external forces are removed then due to internal reactive forces the substance regains its original configuration. Internal reactive forces are also called restoring forces. Restoring forces are equal in magnitude to the external forces but opposite in direction. In equilibrium position; the internal reactive force or the restoring force per unit cross sectional area originated due to strain is called stress.
Question 4.
What is strain?
Answer:
When deforming force is applied an any object then there is change in its length or volume or shape. The proportional change produced in the shape and size of an object due to the deforming force is called strain. It is a dimensionless quantity. According to deformation strain have a three types.
(a) Longitudinal strain
(b) Volume strain
(c) Shearing strain
Question 5.
What do you understand by limit of elasticity?
Answer:
It is the maximum value to deforming force under which an object acts as an elastic body i. e. , when the applied force is removed, the body regains its original position. If force beyond this value is applied on an object, it undergoes permanent deformation.
Question 6.
What is Poisson’s ratio?
Answer:
Poisson’s ratio is defined as the ratio between lateral strain to longitudinal strain, within the elasticity limit. It is represented by σ.
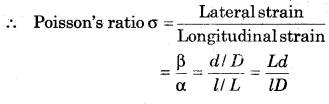
Question 7.
Write the Hooke’s law.
Answer:
According to Hooke’s law, within the limit of elasticity, the stress is proportional to strain.
Streps ∝ Strain
or Stress = E × Strain.
Here E is a constant known as modulus of rigidity. Its unit is same as that of stress.
Question 8.
What do you understand by the rigidity of a solid?
Answer:
For solids the modulus of elasticity is very high hence they are less compressible or more rigid. Therefore, to generate small difference in length of these materials more force is required. Steel is more elastic than copper, brass or aluminium.
Question 9.
What do you understand by the perfectly elastic, plastic and rigid bodies? Discuss their limits.
Answer:
Perfectly elastic bodies: Those bodies which regain their original configuration immediately and completely after the removal of deforming force are called perfectly elastic bodies.
Perfectly plastic bodies: Bodies which do not regain their original configuration at all on the removal of deforming forces are called perfectly plastic bodies. Generally no body is perfectly elastic and perfectly plastic; but they are between these two extremes. Normally, quartz is perfectly elastic body and putty, wax are perfectly plastic bodies.
Rigid bodies: Bodies which do not get deformed or have very small deformation on applying external force are called rigid bodies.
Class 11 Physics Chapter 10 Long Answer Type Questions
Question 1.
Explain stress, strain, limit of elasticity and describe various strains produced in a material.
Answer:
A substance is in equilibrium position in its original form due to the effect of interatomic forces. When external force is applied on any substance then as a result there is change in the shape or size or both of the substance and internal reactive force is produced in the substance. When external forces are removed then due to internal reactive forces the substance regains its original configuration. Internal reactive forces are also called restoring forces. Restoring forces are equal in magnitude to the external forces but opposite in direction. In equilibrium position; the internal reactive force or the restoring force per unit cross sectional area originated due to strain is called stress. In the position of equilibrium the value of reactive force is equal to the external force applied on a unit area; i.e.,

If A is the area of cross section of the body and working external force is F, then;
Stress = F/A
The unit of stress in M.K.S. system is N.m-2 (Newton/metre2) and its dimensional formula is [M1L-1T-2].
When any external force works on a solid then its dimensions can be changed in three types. Hence, stress are of three types :
(a) Longitudinal stress
(b) Normal (volume) stress.
(c) Shearing (Tangential) stress.
(a) Longitudinal Stress : When the deforming force is applied along the length of an object such as a cylinder, then the reactive force acting on the longitudinal cross sectional area of the object is called longitudinal stress. If the length increases in the direction of force then restoring force is called tensile stress and in case of compression it is called compressive stress. In both the cases the length of the cylinder changes. If F is the force acting on the cylinder and its cross sectional area is A then;
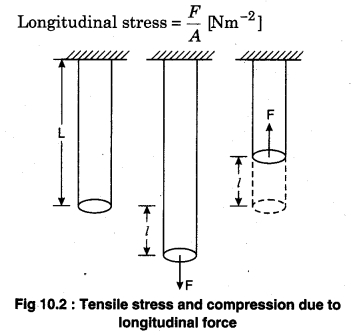
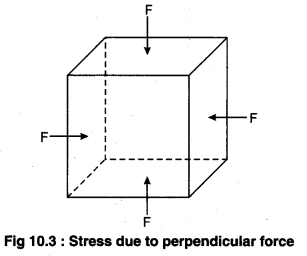
(b) Normal (volume) Stress : When uniform force is applied in the perpendicular direction to the surfaces of an object; then there is change produced in the volume. The reactive normal force in unit area acting opposite to the change in volume is called normal stress. If the volume decreases then it is called compressive stress and if the volume increases it is called tensile stress.
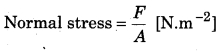
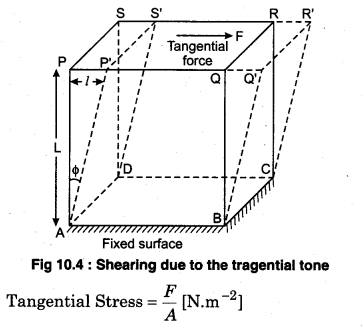
(c) Tangential Stress or Shearing Stress : If one surface of a body is kept stable (by frictional force) and a deforming linear force F is applied on a surface opposite to it (as shown in diagram 10.4); then the perpendicular surface to the stable surface rotates by angle Φ due to which there is change in shape of the body. Due to tangential force shearing stress is produced.
The tangential reactive force applied in unit area opposite to shearing is called tangential stress or shearing stress. This stress is produced in the body due to change or distortion. If tangential force is F working on a cross sectional area A then;
When deforming force is applied an any object then there is change in its length or volume or shape. The proportional change produced in the shape and size of an object due to the deforming force is called strain. It is a dimensionless quantity. According to deformation strain have a three types.
(a) Longitudinal strain
(b) Volume strain
(c) Shearing strain
(a) Longitudinal Strain : The change produced in the unit length or the proportional change produced in the length of an object due to the effect of external force is called longitudinal strain
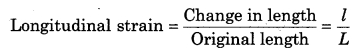
If the length of the object increases after applying external force then it is called tensile strain and if the length of the object decreases after applying external force it is called compressive strain.
(b) Volume Strain : The change produced in the unit volume of the object after applying external force is called volume strain. If ∆V is the change in volume of an object of volume V then;
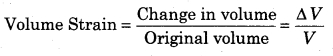
Volume strain is less in solids and liquids but is more in gases.
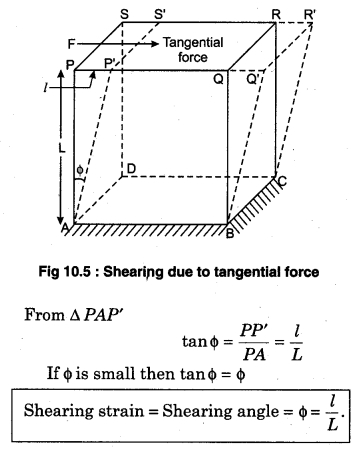
(c) Shearing Strain : If there is change only in th form or shape of an object by applying external tangential force and the length and volume remain unchanged then this type of strain is called shearing strain.
In the figure (10.5) surface ABCD is stable and force F is acting on surface PQRS, due to which surface PQRS deviates by angle Φ from stable surface ABCD. Angle Φ is called shearing angle and it is the measure of shearing strain.
Question 2.
Explain elasticity, limit of elasticity, yield point and breaking point.
Answer:
In any material stress is produced by strain which is produced by the deforming forces. To develop the relationship between strain and stress a graph is drawn between stress and strain. Figure (10.6) shows the curve between stress and strain for a given material under the tensile stress.
For different materials the stress-strain curves area are different. With the help of these curves we can understand that for any given material how it is deformed with the increasing load. We see in the curve that from O to E the relationship is linear meaning that in this area Hooke’s law is followed. When applied force is removed then the object again takes its original position. In this area the solid behaves as an elastic material.
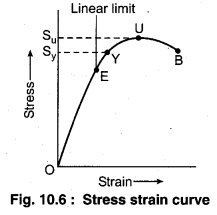
After point E the graph becomes curved. This shows that stress is not directly proportional to strain but strain becomes more. But till point Y the material has the property of elasticity. In the curve point Y is called Yield point or Elastic limit. Elastic limit is close to linear limit. Relative to yield point the value of stress is Sy.
Ahead of point Y, if the weight is increased in the wire the length of the wire increases rapidly. In this situation after removing the weight the wire does not come to its original position, but its length increases. The part between Y and U of the curve shows this. In this situation when stress is zero then also strain is not zero. Then it is stated that there is permanent deformation in the material. This deformation is called plastic deformation. On the graph point U is the maximum limit of tensile. After reducing applied force after this point additional strain is produced and it breaks at point B. If the maximum limit point U and breaking point B are close together then the material is said to be brittle.
If they are far apart, the material is said to be tensile. Sometimes, after removing the external force in elasticity limit the material does not come to its original position but returns after sometime. This lag in time interval is called Elastic relaxation and time is called Elastic relaxation time.
It is also seen that when the external deforming force is increased or decreased then the strain does not change with the applied force. The lagging of strain’ from the applied force is called Elastic Hysteresis. Due to elastic hysteresis there is loss of energy which is seen in the form of heat.
Question 3.
Explain stress, strain and modulus of elasticity and define Young’s modulus of elasticity.
Answer:
A substance is in equilibrium position in its original form due to the effect of interatomic forces. When external force is applied on any substance then as a result there is change in the shape or size or both of the substance and internal reactive force is produced in the substance. When external forces are removed then due to internal reactive forces the substance regains its original configuration. Internal reactive forces are also called restoring forces. Restoring forces are equal in magnitude to the external forces but opposite in direction. In equilibrium position; the internal reactive force or the restoring force per unit cross sectional area originated due to strain is called stress.
When deforming force is applied an any object then there is change in its length or volume or shape. The proportional change produced in the shape and size of an object due to the deforming force is called strain. It is a dimensionless quantity. According to deformation strain have a three types.
(a) Longitudinal strain
(b) Volume strain
(c) Shearing strain
The ratio of longitudinal stress to longitudinal strain is called Young’s modulus of elasticity in elasticity limit. It is represented by Y.
Young’s modulus of elasticity

If on any wire of longitudinal cross sectional area A a tensile force F is applied then its initial length L and change in length is l, then;

The value of Y is calculated only for solids and it is a characteristic of solids.
Question 4.
What is Poisson’s ratio? Define its limits.
Answer:
When force is applied on any wire along its length then its length increases and along perpendicular direction the width of the wire decreases.
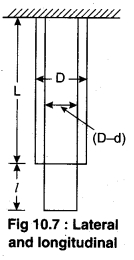
This way we can say that by applying deforming force two types of strains are generated in the direction of force longitudinal strain and lateral strain both are generated together. If longitudinal strain is represented as a and transverse or lateral strain is represented as β then;

Poission’s Ratio is defined as the ratio between lateral strain to longitudinal strain; within the elasticity limit. It is represented by σ.
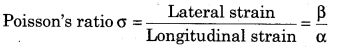
If in any material when force F is applied in the direction of length L;then change in the length is l and change in width D is d then;

Since, Poisson’s ratio is the ratio of two strains, hence it is dimensionless quantity.
Generally, the value of Poisson’s ratio ranges from -1 to + 0.5. Normally, the value of σ is between 0.2 to 0.4 [For Steel, σ = 0.19, Copper σ = 0.32 and for Brass it is σ = 0.26. ]
Question 5.
Define Young’s modulus of elasticity, modulus of rigidity and Bulk modulus of elasticity. Calculate Young’s; modulus of elasticity by Searle’s experiment method.
Answer:
The ratio of longitudinal stress to longitudinal strain is called Young’s modulus of elasticity in elasticity limit. It is represented by Y.
Young’s modulus of elasticity

If on any wire of longitudinal cross sectional area A a tensile force F is applied then its initial length L and change in length is l, then;

The value of Y is calculated only for solids and it is a characteristic of solids.
When on every point of the surface of any object a perpendicular and equal force i. e., pressure is applied then the volume of the object changes but the nature or form does not change. This type of strain can be in all the three types of states of any material such as solid, liquid and gas. The change in the unit volume of the object is called ‘volume strain’ and the normal force (pressure) applied on unit area of the object is called ‘normal stress’. In the limit of elasticity the ratio of normal stress to volume strain is called bulk modulus of elasticity. It is represented by K.
![]()
If the material having surface area A; an equal normal deforming force F is applied on all the surfaces of the material; then due to this there is no change in the shape of the material but there is AV change in the original volume V then;
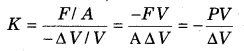
Negative sign shows that if pressure is increased then volume decreases and when pressure is decreased then volume increases i. e., the signs of P and ∆V are opposite.
Inverse of bulk modulus of elasticity is called compressibility. Therefore;
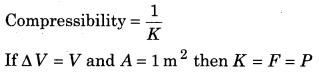
Hence, by quantitative form within the limit of elasticity the perpendicular and uniform applied force on any unit transverse cross sectional area; by which the volume of the object reduces to half of its initial volume; is equal to the bulk modulus of elasticity of that material.
For solids the value of bulk modulus of elasticity is very high than liquids and for liquids the value is much higher than gases. In this way solids are less compressible and gases are more compressible.
It is defined as the ratio of tangential stress to the shearing strain; within the elastic limit. It is represented by η.

From table 10.1 we understand that the value of modulus of rigidity (η) is less than Young’s modulus of elasticity (Y) i.e., stretching or compressing an object (material) is more tough than deforming its shape.
For metals, Young’s modulus of elasticity is more. Therefore, to generate small difference in length of these materials; more force is required. Steel is more elastic than copper, brass and aluminium. Due to this reason the machines used for heavy works and structural designs give more preference to steel.
Set Before Numerical Examples
Factors Affecting Elasticity
The elasticity of a material is affected by the following factors :
(i) Effect of annealing : Annealing means heating and then cooling gradually. The process of annealing results into the formation of larger crystal gains. Here, the elasticity of the material decreases.
(ii) Effect of the impurities present in the material : The elasticity of the material can be increased or decreased by adding impurities in it depending on the nature of impurities.
(iii) Effect of hammering and rolling : Hammering and rolling leads to breaks up the crystal grains into the smaller peices. Thus the elasticity of the materials is increased.
(iv) Effect of temperature : The elasticity of the materials decrease with increase in temperature.
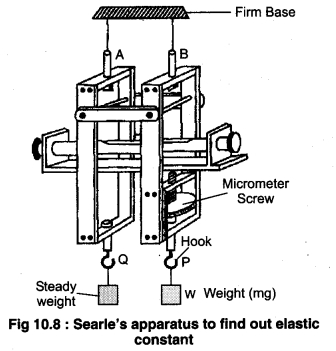
In Searle’s experiment there is a rectangular frame of metal. As shown in figure (10.8) on a rigid base two wires A and B of same material have hook P and Q hanged. One end of the spirit level is attached to the frame P and second end is at the screw of the spherometer. The spherometer screw can be rotated up and down along a vertical pitch and along with it rotates the spirit level. The hanged weight W from hook P is a stable weight which does produce twist in the wire. The hook from Q has a hanger.
When any weight is placed on the string (wire) A then its length increases and the independent end of spirit level moves downwards. By rotating the spherometer the spirit level is brought in the horizontal position. By reading the initial reading and the final reading the distance travelled by the spherometer is calculated. This distance is the increased length due to weight.
For different weights by experiment the increase in length is calculated. A graph is drawn by taking weight (M) on X-axis and increase (l) on Y-axis.
Suppose, the initial length of the wire A is L and applied mass is M, r is the radius of the wire and increase in length is l then;
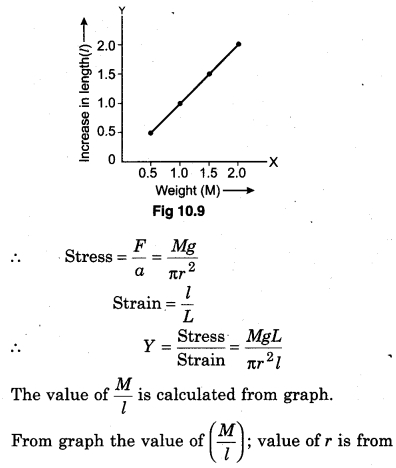
screw gauge and value of L from metre scale can be calculated and kept in the formula and the value of Young’s modulus of elasticity is calculated.
The weight applied should not be more than the limit of elasticity. The limit of elasticity is dependent on the material and its radius.
Question 6.
Define elastic stress. If length of any wire is increased by applying external force then prove that the work done on per unit volume of wire = 1/ 2 × stress × strain.
Answer:
In equilibrium state the potential energy of a body is minimum or zero. But when external force is applied on a body then the internal reactive force is produced in the body; which “resists the positional change. The work done opposite to the internal reactive force by the external force increases the potential energy of the body. This energy is known in the form of elastic energy.
When we stretch any wire (string) then we do some work stored opposite to the interatomic force; which is stored in the string in the form of elastic potential energy. Suppose, by applying a force F on a string of length L its length increases by l. Initially the internal force in the string was zero, but as the length increases the internal force increases from zero and becomes equal to the applied force F. In this way the average internal force for increasing the length of the string to l;
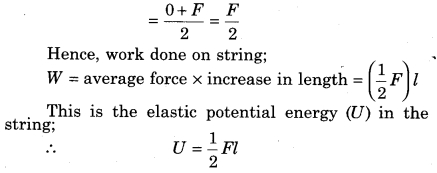
If the initial length of the wire is L and transverse or lateral cross sectional area is A; then again writing the above equation;
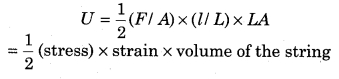

Class 11 Physics Chapter 10 Numerical Questions
Question 1.
Tn a wire by producing 4 × 10-4 linear strain a 4.8 × 107 Nm-2 stress is produced. Calculate the Young’s modulus of elasticity of the material.
Solution:

Question 2.
The average depth of Indian Ocean is 3 km. Calculate
![]()
given that the Bulk modulus of elasticity for water is 2.2 × 109 Nm-2, (g = 10 m/s2).
Solution:
Given, average depth of Indian ocean, h = 3 km
Bulk modulus of elasticity of water, K = 2.2 × 109 Nm-2 and g = 10ms-2
∴ Pressure, P = hpg = 3 × 103 × 103 × 10
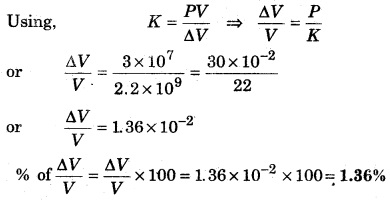
Question 3.
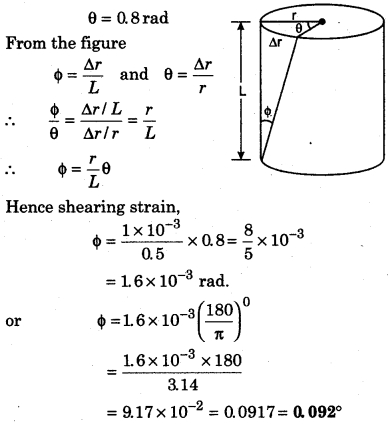
A wire of length 0- 5 m and diameter 2 mm is tied at one end and is twisted at the other end by 0.8 rad. Calculate the shearing strain on the surface of the wire.
[Hint: Shearing strain Φ = \(\frac { r }{ l } \) Φ ]
Solution:
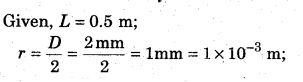
Question 4.
A copper wire of length 2.2 m and a steel wire of length 1.6 m both of whose diameters are 3.0 nun are tied at end. When it was stretched by a weight then the total increase was 0.7 nun. Calculate the value of the applied weight.
Solution:
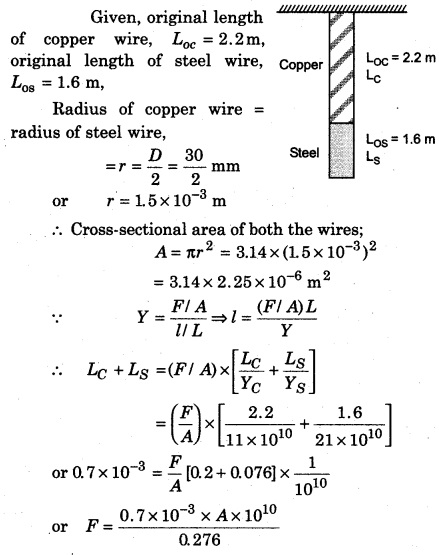
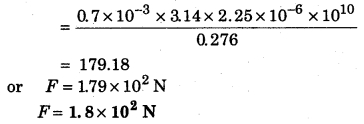
Question 5.
A 5 m long steel rod is tied between two rigid bases. Steel’s linear modulus of elasticity = 12 × 10-6 l°C and Y = 2 × 1011 Nm-2. Calculate the stress produced in the rod if the temperature is increased by 40°C.
[Hint : Increase in length l = α L t]
Solution:

Question 6.
How much will be the work done in stretching a 2 m long wire of area 1 mm2 by 0.1 nun?
[Hint: Work done = \(\frac { 1 }{ 2 } \) × stress × strain × volume]
Solution:
Given, L = 2m; A = 1mm2 = 1 × 10-6 m2,
l = 0.1 mm = 0.1 × 10-3 m
∵ Work done = \(\frac { 1 }{ 2 } \) × stress × strain × volume
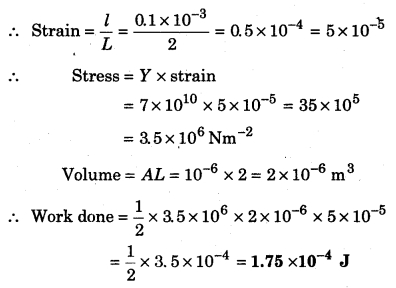
Question 7.
Calculate the Poisson’s ratio when a rubber string is stretched and in that situation the change in its volume is negligible in comparision to the change in shape.
Solution:
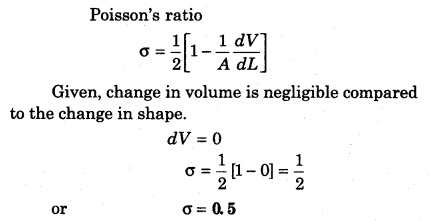
Question 8.
A solid rubber ball when taken from the surface to the bottom of a 200 m deep lake the volume of the ball reduces by 0.1%. Density of water of the lake = 1.0 × 103 kg/m3. Calculate the Bulk modulus of elasticity of rubber, (g = 10 m/s2)
Solution:

Question 9.
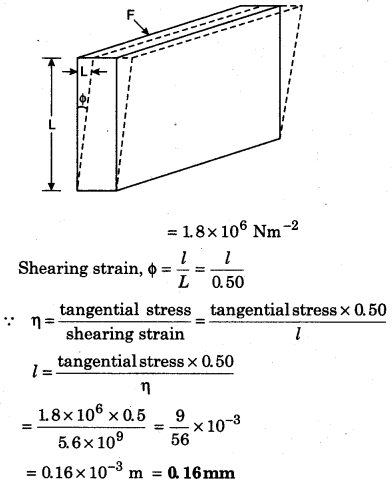
A shearing force of 9.0 × 104 N is applied on a thin surface of a square glass slab of 50 cm side and width 10 cm. Second thin surface is stick to the floor. How much will the upper surface get displaced?
Solution:
Given, F = 9.0 × 104 N, length of slab = 50 cm = 50 × 10-2 m
Width of slab = 10cm = 10 × 10-2 m
∴ Area of slab = 50 × 10-2 × 10 × 10-2
= 5 × 10-2 m2
Modulus of rigidity of glass = 5.6 × 109 Nm-2
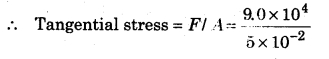
Question 10.
For a steel wire of 4.7 m length and transverse cross section of 3.0 × 10-5 m2 and a copper wire of length 3.5 m and 4.0 × 10-5 m2, the increase in length of both is same when same value of weights are hanged from the wires. What is the ratio of steel and copper’s Young’s modulus of elasticity?
Solution:
Length of steel wire Ls = 4.7 m
Cross-section area of steel wire
As =3.0 × 10-5 m-2
Length of copper wire LC = 3.5 m
Cross-section area of copper wire
AC = 40 × 10-5 m2
Let Young’s modulus of elasticity for steel and copper be Ys and Yc
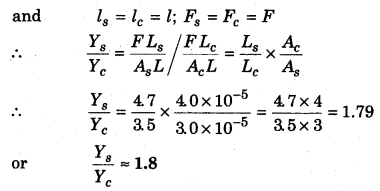
Question 11.
Two wires are made up of the same material (metal). Length of the first wire is half the length of the second wire, and its diameter is double the diameter of the second wire. If same weights are hanged from the wires then what would be the ratio of increase in the length of the wires?
Solution:
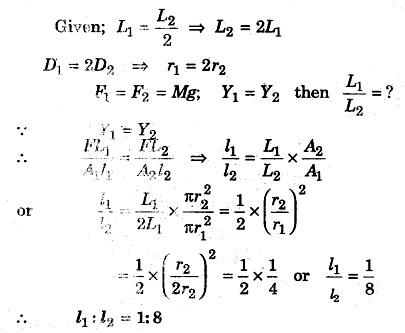
Question 12.
A material breaks by the stress of 109 N.m-2; if the density of the material is 3 × 103 kg m-3 then calculate that length of the wire; which on hanging by its own weight breaks.
Solution:

Question 13.
The ratio of radius of two wires of same material is 2 : 1 If they are stretched by applying similar force then what would be the ratio of the stress generated?
Solution:
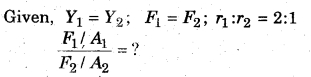
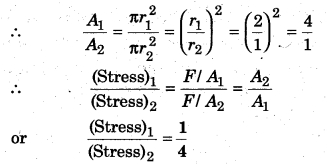
Question 14.
From any rigid base a steel wire of length 2 m and weight 3g a weight of 2.5 kg is hanged. The increase in length of the steel wire is 2.5 mm. If the density of the steel wire is 7.8 × 103 kg/m3 then calculate the Young’s modulus of elasticity.
Solution:
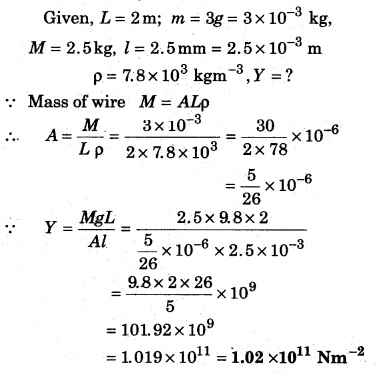
Question 15.
A copper wire of transverse cross section of 0.8 cm2 is tied at both the ends rigidly. If the temperature of the wire is reduced by 20°C then calculate the tension in the wire. Young’s modulus of elasticity of copper is 11 × 1010 Nm-2 and coefficient of expansion is 17 × 10-6/°C.
Solution:
Tension in the wire due to reduction in temperature
Given, F = YAα∆θ
Y = 11 × 1011 Nm-2;
A = 0.8cm2 = 0.8 × 10-4 m2;
α = 1.7 × 10-6 oC-1; ∆θ = 20°; F = ?
∴ F = 11 × 1011 × 0.8 × 10-4 × 1.7 × 10-6 × 20
= 8.8 × 3.4 × 102
= 29.92 × 102 = 2992 N