Rajasthan Board RBSE Class 11 Physics Chapter 13 Thermodynamics
RBSE Class 11 Physics Chapter 13 Textbook Exercises With Solutions
RBSE Class 11 Physics Chapter 13 Very Short Answer Type Questions
Question 1.
If two systems A and B are in thermal equilibrium with C, then will A and B also be in thermal equilibrium?
Answer:
Yes; according to Zeroth law of Thermodynamics.
Question 2.
On which law is the first law of thermodynamics based on?
Answer:
Law of conservation of energy.
Question 3.
Write the Mayer’s relation.
Answer:
Mayer’s relation ⇒ Cp – Cv = R
where R = universal gas constant
Cp = molar specific heat at constant pressure
Cv = molar specific heat at constant volume
Question 4.
Write the P-V relation for adiabatic expansion of ideal gas.
Solution:
PVγ = constant, where γ = \(\frac { { C }_{ p } }{ { C }_{ v } } \) which is known as atomicity of gas
Question 5.
What are the dimensions of efficiency of heat engine?
Answer:
Efficiency of heat engine,
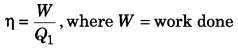
Q1 = heat taken out from source.
∵ W and Q have same unit,
∴ efficiency η is dimensionless.
∴ Dimensional formula for η
= [M0L0T0]
Question 6.
What is the effect on pressure on change of state in a system in an isobaric process?
Answer:
Answer:
In an isobaric process, the pressure remains constant hence the change in pressure ∆P = 0.
Question 7.
Can heat be supplied without increasing the temperature of gas?
Answer:
Yes, when the gas is allowed to do the work on the surroundings.
Question 8.
Which thermodynamical variable is defined by the Zeroth law of Thermodynamics?
Answer:
Temperature.
Question 9.
What is the specific heat of a gas in isothermal and adiabatic process?
Answer:
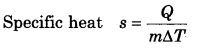
In isothermal process ∆T = 0 ∴s = ∞ (infinity)
and in adiabatic process Q = 0 ∴ s = 0 (zero)
Question 10.
What type of process is a Carnot cyclic?
Answer:
Reversible cyclic process.
Question 11.
On what factors does the efficiency of a Carnot engine depend?
Answer:
Efficiency of a carnot heat engine,
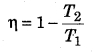
∴ It depends on the temperatures of source and sink.
RBSE Class 11 Physics Chapter 13 Short Answer Type Questions
Question 1.
Reversibility is the basis of an ideal engine. Briefly explain the statement.
Answer:
In a reversible process, the system and its surroundings return to the original states if the forward cycle is followed by the reverse cycle. Carnot engine is a theoretical thermodynamical cycle proposed by Leonard Carnot. It gives the estimate of the maximum possible efficiency that a heat engine during the conversion process of heat into work and conversely, working between two reservoirs can possess. Thus we can say that reversibility is the basis of an ideal engine.
Question 2.
Explain the efficiency of heat engine.
Answer:
For a heat eng`ine, the total thermodynamical process is generally irreversible. The ratio of work done to convert heat and the heat absorbed by the source is called efficiency.

From the above relation, it is clear that the efficiency of engine depends upon the temperature of source (T1) and sink (T2).
Here T1 > (T1 – T2). Efficiency is always less than one, i. e., less than 100%.
If T1 = T2, then η = 0, which represents that when source and sink are at same temperature. Then, in this situation, heat energy can not be transformed to mechanical energy. It is to be noted here that the value of η will be 100% in two situations : if T1 = ∞ or T2 = 0, and both these situations are not possible. So, efficiency can not be 100%.
Question 3.
What is Thermodynamics? Explain the Zeroth law of Thermodynamics and give its importance.
Answer:
Principle : It is based on the principle of temperature.
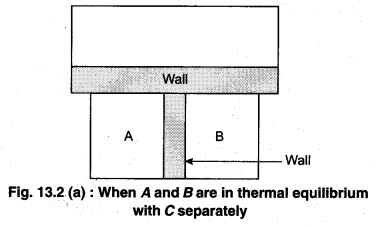
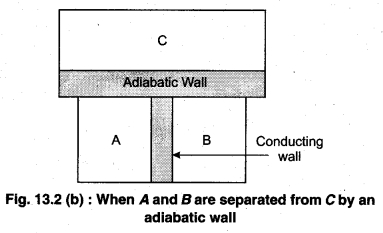
To understand this law, consider two systems A and B, separated by an adiabatic wall, each of these are in contact with a third system C by a conducting wall. The states of the system will change until A and B are in equilibrium with C. Now, let the adiabatic wall between A and B be replaced by a conducting wall and C is insulated from A and B by an adiabatic wall. It is found that A and B are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.
The zeroth law apparently suggests that when two systems A and B are in thermal equilibrium, then, there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature (T). If A and B are separately in equilibrium with C, then, TA = TC and TB = TC – This means that TA = TB. So, the systems A and B are in thermal equilibrium.
Question 4.
Explain heat, work and internal energy of a system.
Answer:
Temperature determines the direction of flow of heat when two bodies are in thermal contact. Heat flows from the body at a higher temperature to a lower temperature. The flow stops when the two bodies are in thermal equilibrium. This type of heat transfer is a non-mechanical energy transfer.
When thermal energy is transferred from an object into the atmosphere then the thermal energy of the object is taken to be negative while on giving heat to an object from the atmosphere the thermal energy of the object is taken to be positive. If the temperature of the object remains constant then due to the exchange of heat in the object the state of the object changes.
Question 5.
Explain the work done in an isothermal process.
Answer:
Essential conditions for an isothermal process:
(i) The process of compression or expansion should be infinitely slow. So as to provide a sufficient time for the exchange of heat.
(ii) The walls of the container must be perfectly conducting to allow free exchange of heat between container and surroundings.
Consider a cylinder with µ, moles of an ideal gas at isothermal expansion, then it reaches its final state (P2, V2) from initial state (P1, V1). Meanwhile, in the stage when pressure is P and change in volume is V + dV from V, then pressure (P).
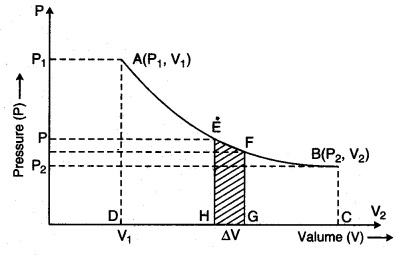

Since pressure and volume are inversely proportional to each other in an isothermal process, then from equation (13.20 a), from Boyle’s law for ideal gas
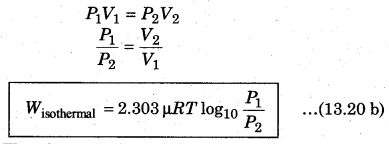
The above expression shows the work done for p moles of an ideal gas in an isothermal process. State equation for isothermal process,
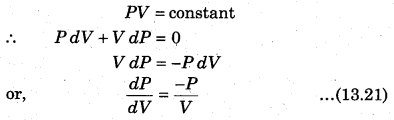
The slope for P.V curve in an isothermal process is negative.
Question 6.
Explain the First Law of Thermo-dynamics.
Answer:
According to figure 13.6, consider a cylinder with n moles of ideal gas made of completely insulated material in which a frictionless insulated piston is placed. Let the pressure of gas be P and the area of cross-section of piston be A If piston is moved upwards by a distance dx, i.e:, the work done by the gas on expansion of the gas,
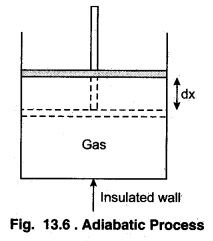
dW = P A dx = P dV …(13.33)
Here, dV = Adx represents the increase in the volume. Now, let the gas expands adiabatically and the initial state (P1 V1 T1) becomes final state (P2, V2, T2). Then, the total work done by the gas
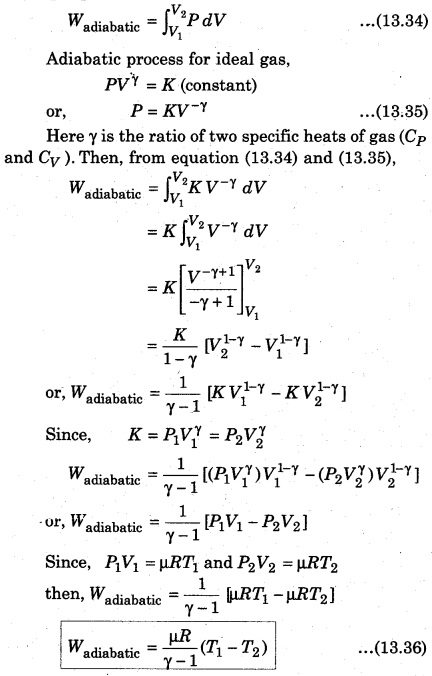
The above expression shows that work done by p moles of an ideal gas in adiabatic process. It is clear that if work is done by the gas, then the value of Wadiabatic is positive and it is possible when T1 > T2. When gas is compressed, work is done on the gas, then the value of Wadiabatic is negative and it is possible when T1 < T2, i. e., there is increase in the temperature of gas.
Question 7.
Derive the Mayer’s relation.
Answer:
Consider one mole of an ideal gas. Let dQ be the amount of heat is given to the system to raise the temperature by dT, and change in internal energy be dV. Then, from first law of Thermodynamics,
dQ = dU + PdV …(13.14)
If heat is supplied to one mole at constant volume, i.e.,
V = constant,
then, dV = 0
From equation (13.14),
dQ = dU …(13,15)
Molar specific heat (CV ) at constant volume,
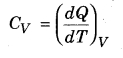
From equation (13.15),
dQ = dU = Cv dT …(13.16)
If one mole of gas is supplied heat at constant pressure, i.e., from equation (13.13) of molar specific heat Cp at constant pressure,
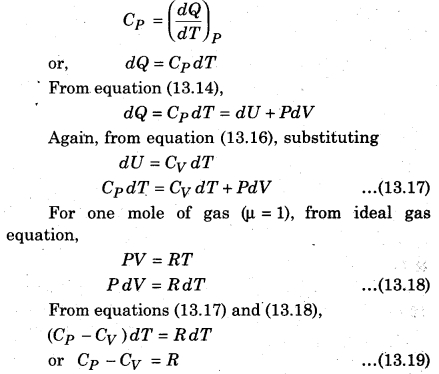
The above expression is called Mayer’s relation where R = 8.31 J.mol-1 K-1. This relation is for one mole of gas.
Question 8.
Differentiate between reversible and irreversible process.
Answer:
Reversible Process :
- The process is carried out infinitesimally slowly
- At any stage, the equilibrium is not disturbed
- It takes infinite time for completion.
- Work obtained in this process is maximum.
Irreversible Process :
- It is carried out rapidly
- Equilibrium may exist only after the completion of the process.
- It takes a finite time for completion.
- Work obtained in this process is not maximum
Question 9.
Explain the work done by gas in an adiabatic expansion.
Answer:
Adiabatic process is that process in which temperature (T), pressure (P) and volume (V) can be changed, but there is no transfer of heat between a thermodynamical system and its surroundings. In this process, energy is transferred only as work. This process provides a rigorous conceptual basis to explain the first law of Thermodynamics.
A process in which transfer of heat is not involved in the system, so that Q = 0, is called an adiabatic process. For example, the compression of a gas within an engine’s cylinder is assumed to take place so fast that on the time scale of the process of compression, little energy of the system can be transferred out as heat.
Essential conditions for an adiabatic process:
- The process of expansion or compression should be sudden, so that heat does not get time to get exchanged with the surroundings.
- The walls of the container must be perfectly insulated so that there cannot be any exchange of heat between the gas and surroundings.
Question 10.
Derive the formula for efficiency of Carnot engine.
Answer:
In 1824 scientist Sadi carnot imagined a theoretical engine by which the heat taken from high temperature object when changed completely into useful work then the efficiency of the engine will be more. Carnot tried to find out if the maximum efficiency of an engine could be 100%. An ideal reversible heat engine working between two temperatures is called carnot’s engine.
Carnot Cycle : In carnot’s engine, starting from a definite state of working material passing through different reversible processes again gaining the initial position is called carnot cycle. Carnot engine has following parts :
(i) Working substance
(ii) Source
(iii) Insulating Stand
(iv) Sink
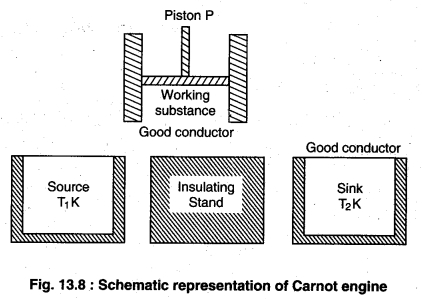
(i) Working substance: The substance by which work is done is called working substance. In carnot engine ideal gas is taken as working substance in a cylinder with a friction less piston P.
(ii) Source: This is an object of high temperature whose temperature T1K is constant. Is heat capacity should be infinite so that if the takes heat is no change in its temperature.
(iii) Insulating Stand: This is a completely non conducting object on which the working substance is kept and passed through adiabatic process.
(iv) Sink: This is a low temperature object with constant temperature T2K. It shodld also have infinite heat capacity so that on giving heat to its temperature does not change.
Question 11.
Derive the formula for the efficiency of carnot heat engine and explain it.
Answer:
For a heat engine, the total thermodynamical process is generally irreversible. The ratio of work done to convert heat and the heat absorbed by the source is called efficiency.

From the above relation, it is clear that the efficiency of engine depends upon the temperature of source (T1) and sink (T2).
Here T1 > (T1 – T2). Efficiency is always less than one, i. e., less than 100%.
If T1 = T2, then η = 0, which represents that when source and sink are at same temperature. Then, in this situation, heat energy can not be transformed to mechanical energy. It is to be noted here that the value of q will be 100% in two situations : if T1 = ∞ or T2 = 0, and both these situations are not possible. So, efficiency can not be 100%.
RBSE Class 11 Physics Chapter 13 Long Answer Type Questions
Question 1.
Explain briefly the zeroth, first and second law of Thermodynamics.
Answer:
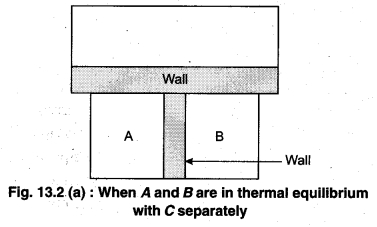
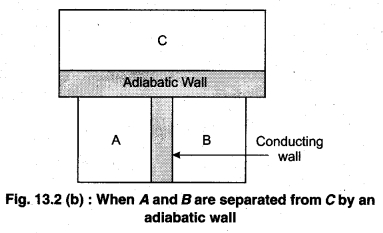
Principle : It is based on the principle of temperature.
To understand this law, consider two systems A and B, separated by an adiabatic wall, each of these are in contact with a third system C by a conducting wall. The states of the system will change until A and B are in equilibrium with C. Now, let the adiabatic wall between A and B be replaced by a conducting wall and C is insulated from A and B by an adiabatic wall. It is found that A and B are in thermal equilibrium with each other. This is the basis of Zeroth law of thermodynamics. This law states that the two systems are in thermal equilibrium with a third system separately, then both are in thermal equilibrium with each other.
The zeroth law apparently suggests that when two systems A and B are in thermal equilibrium, then, there must be a physical quantity that has the same value for both. The thermodynamic variable whose value is equal for the two systems (in thermal equilibrium) is called temperature (T). If A and B are separately in equilibrium with C, then, TA = TC and TB = TC – This means that TA = TB. So, the systems A and B are in thermal equilibrium.
The first law of thermodynamics states the equivalence of heat and work. This law is based on the principle of conservation of energy.
The internal energy U of a system can change through two modes of energy transfer : heat and work.
Let ∆Q = Heat supplied to the system by the surroundings,
∆W = Work done by the system on the surroundings.
∆U = Change in internal energy of the system.
From the general principle of conservation of energy, i.e..
∆Q = ∆U + ∆W …(13.9)
The energy ∆Q, supplied to the system goes in partly to increase the internal energy of the system (∆U) and work (∆W). Equation (13.9) is called the first law of Thermodynamics. This is the general law of conservation of energy applied to any system in which the energy transfer from or to the surroudnings.
We can write equation (13.9) as
∆Q – ∆W = ∆U …(13.9a)
Now, the system go from an initial state to final state in a number of ways.
To change the state of a gas from (P1,V1) to (p2, V2), we first change the volume from V1 to V2, keeping the pressure constant. This means that we first go to state (P1 ,V2) Changing the pressure from P1 and P2, keeping volume constant to the state (P2,V2). We can also first keep the volume constant and then keep the pressure constant.
U is a state variable. ∆U depends only on the initial and final states and not on the path taken by the gas to .move from one to the other. However ∆Q and ∆W depends on the path in moving from initial to final states.
From equation (13.9 a), (∆Q – ∆W) is path independent for a system with ∆U = 0,
∆Q = ∆W
This implies that heat supplied to the system is completely used up by the system in doing work on the environment. Work done by the system against a constant pressure P is
∆W = P∆V
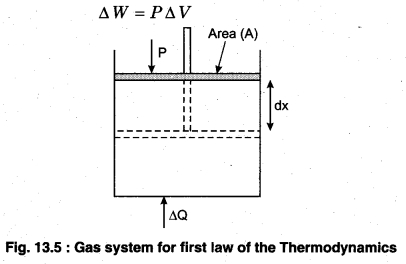
Here, ∆V is the small change in volume of gas.
Sis, equation (13.9 a) gives
∆Q = ∆U + P∆V …(13.9 b)
The second law of Thermodynamics states that the total entropy of an isolated system increases over time, or it remains same in ideal cases (where the system undergoes a reversible process or when it is in a steady state). The first law of Thermodynamics tells the basic definition of internal energy and states the law of conservation of energy. The second law of Thermodynamics deals with the direction of natural process. It states that a natural process is not reversible. For e.g., heat flows from hot to cold region, and never the reverse, unless some external work is done on the system.
In Terms of Entropy
In a reversible process, a very small increase in the entropy (dS) of a system is defined to result from a small heat transfer to a closed system divided by the common temperature (T) of the system and the surroundings that supply of the heat :
dS = \(\frac { dQ }{ T } \) (closed system)
Question 2.
Explain the various processes of thermodynamics and work done in these processes.
Answer:
Every equilibrium state of a thermodynamical system is completely described by specific values of some macroscopic variables. If in a thermodynamic system, variables like temperature (T), pressure (P), volume (V), etc. changes with time, then the process is called thermodynamical process. There are various types of thermodynamical processes :
(i) Isothermal process
(ii) Isochoric process
(iii) Isobaric process
(iv) Adiabatic process
(v) Cyclic process
(i) Isothermal process :
An isothermal process is a change of a system, in which the temperature remains constant, ∆T = O.This typically occurs when a system is in contact with an outside thermal reservoir and the change takes place slowly to allow the system to continually adjust to the reservoir’s temperature through heat exchange.
Isothermal process takes place in any type of system that regulates the temperature. In the thermodynamic analysis of chemical reactions, it is first analyzed what happens under isothermal conditions. In an isothermal process, the internal energy of an ideal gas is constant. This is due to the fact that there are no intermoleculaf forces in an ideal gas. In the isothermal compression’of a gas, there is work done on the system to decrease the volume and increase the pressure. Doing work on the gas, can increase the internal energy and increase the temperature. For constant temperature, energy must leave the system. For an ideal gas, the amount of energy entering the environment is equal to the amount of work done on the gas, as the internal energy does not vary.
(ii) Isochoric process :
If in a physical change of thermodynamic system, there is change in pressure (P) and temperature but volume remains constant, then, it is called an isochoric process. So, no work is done by the gas in this process. No work is done on the gas because V is constant. Then, dV = 0
(iii) Isobaric process :
If temperature (T) and volume (V) changes in a physical change in a thermodynamic system and pressure (P) is constant, the process is called isobaric i.e, when the state of the substance changes, then the pressure (P) is constant. For example, freezing of water, formation of steam, etc.
(iv) Adiabatic process :
Adiabatic process is that process in which changed, but there is no transfer of heat between a thermodynamical system and its surroundings. In this process, energy is transferred only as work. This process provides a rigorous conceptual basis to explain the first law of Thermodynamics.
A process in which transfer of heat is not involved in the system, so that Q = 0, is called an adiabatic process. For example, the compression of a gas within an engine’s cylinder is assumed to take place so fast that on the time scale of the process of compression, little energy of the system can be transferred out as heat.
Essential conditions for an adiabatic process :
- The process of expansion or compression should be sudden, so that heat does not get time to get exchanged with the surroundings.
- The walls of the container must be perfectly insulated so that there cannot be any exchange of heat between the gas and surroundings.
(v) Cyclic process :
The process of thermodynamics in which system undergoes various changes and comes back to the initial state, is called a cyclic process. In this process, dU = 0. Since, internal energy is a function of state. Now, according to the first law of Thermodynamics:
dQ = dU + dW
dQ = 0 + dW
dQ = dW
This means that the total absorbed heat in the system is equal to the work done by the system.
Question 3.
Differentiate between the isothermal and adiabatic processes and calculate the work done in these process.
Answer:
An isothermal process is a change of a system, in which the temperature remains constant, ∆T = O.This typically occurs when a system is in contact with an outside thermal reservoir and the change takes place slowly to allow the system to continually adjust to the reservoir’s temperature through heat exchange.
Isothermal process takes place in any type of system that regulates the temperature. In the thermodynamic analysis of chemical reactions, it is first analyzed what happens under isothermal conditions. In an isothermal process, the internal energy of an ideal gas is constant. This is due to the fact that there are no intermoleculaf forces in an ideal gas. In the isothermal compression’of a gas, there is work done on the system to decrease the volume and increase the pressure. Doing work on the gas, can increase the internal energy and increase the temperature. For constant temperature, energy must leave the system. For an ideal gas, the amount of energy entering the environment is equal to the amount of work done on the gas, as the internal energy does not vary.
Adiabatic process is that process in which changed, but there is no transfer of heat between a thermodynamical system and its surroundings. In this process, energy is transferred only as work. This process provides a rigorous conceptual basis to explain the first law of Thermodynamics.
A process in which transfer of heat is not involved in the system, so that Q = 0, is called an adiabatic process. For example, the compression of a gas within an engine’s cylinder is assumed to take place so fast that on the time scale of the process of compression, little energy of the system can be transferred out as heat.
Essential conditions for an adiabatic process :
- The process of expansion or compression should be sudden, so that heat does not get time to get exchanged with the surroundings.
- The walls of the container must be perfectly insulated so that there cannot be any exchange of heat between the gas and surroundings.
Question 4.
Write the working principle of Carnot’s reversible engine and plot the P-V curve for work in each process, and obtain the formula for efficiency.
Answer:
In 1824 scientist Sadi carnot imagined a theoretical engine by which the heat taken from high temperature object when changed completely into useful work then the efficiency of the engine will be more. Carnot tried to find out if the maximum efficiency of an engine could be 100%. An ideal reversible heat engine working between two temperatures is called carnot’s engine.
Carnot Cycle : In carnot’s engine, starting from a definite state of working material passing through different reversible processes again gaining the initial position is called carnot cycle. Carnot engine has following parts :
(i) Working substance
(ii) Source
(iii) Insulating Stand
(iv) Sink
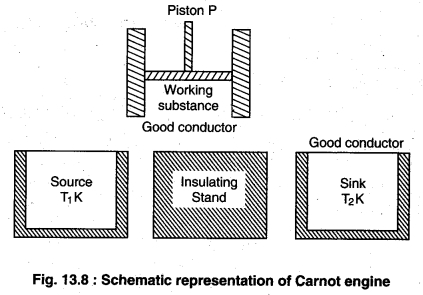
(i) Working substance : The substance by which
work is done is called working substance. In carnot engine ideal gas is taken as working substance in a cylinder with a friction less piston P.
(ii) Source : This is an object of high temperature
whose temperature T1K is constant. Is heat capacity should be infinite so that if the takes heat is no change? in its temperature.
(iii) Stand : This is a completely non conducting object on which the working substance is kept and passed through adiabatic process.
(iv) Sink : This is a low temperature object with constant temperature T2K. It should also have infinite heat capacity so that on giving heat to its temperature does not change.
Question 5.
Write the statements of Kelvin-Planck and Clausius of second law of Thermodynamics and show the equivalence of the two statements.
Answer:
The second law of Thermodynamics states that the total entropy of an isolated system increases over time, or it remains same in ideal cases (where the system undergoes a reversible process or when it is in a steady state). The first law of Thermodynamics tells the basic definition of internal energy and states the law of conservation of energy. The second law of Thermodynamics deals with the direction of natural process. It states that a natural process is not reversible. For e.g., heat flows from hot to cold region, and never the reverse, unless some external work is done on the system.
In Terms of Entropy
In a reversible process, a very small increase in the entropy (dS) of a system is defined to result from a small heat transfer to a closed system divided by the common temperature (T) of the system and the surroundings that supply of the heat :
dS = \(\frac { dQ }{ T } \) (closed system)
Various Statements of the Planck’s Law :
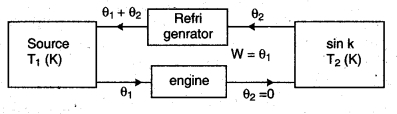
1. Statement of Kelvin : According to this statement “It is not possible to make an engine in which the working substance can take heat from the source and change it completely into .work and remain unchanged itself in one complete cycle.” It is concluded from this statement that it is not possible to get work continuously from heat source. Actually the sink in necessary and it is necessary to release. Some heat to the sink. This statement is based on the principle of carnot heat engine.
2. Statement of Clausius : According to this statement, “It is an impossible process that in cyclic process the working substance transfers heat from low temperature object to high temperature object directly in the absence of external work.”
It is concluded from this statement that transfer of heat from a low temperature object to a high temperature object on its own is not possible. For this it is important that external work be done on the working substance. This statement is based on the principle of refrigerator.
Equivalence of Clausius and Kelvin Statements :
Let there be an engine violating the Kelvin statement : i.e., one that drains heat and converts it completely into work in a cyclic manner without any other result. Now, pairing it with a reverse Carnot engine.
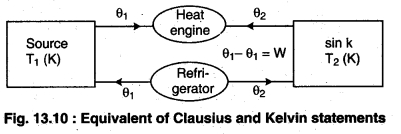
The newly created engine (consists of two engines) transfers heat ∆Q = Q(\(\frac { 1 }{ \eta } \) – 1) from the colder region (sink) to the hotter region (source), which violates the statement of Clausius. Thus, violation of Kelvin statement means violation of Clausius statement i.e., the Clausius statement implies the Kelvin statement. Similarly, we can prove that the Kelvin Statement implies the Clausius statement and hence both the statements are equivalent.
Question 6.
Write and obtain the Carnot’s theorem.
Answer:
Carnot’s theorem states :
(a) All heat engines between two heat reservoirs are less efficient than a Carnot heat engine operating between the same reservoirs. The efficiency of Carnot (reversible) engine is maximum.
(b) The efficiency of and each every Carnot heat engine working between a pair of heat reservoirs are equal, regardless of the working substance employed.
Proof:
Figure 13.11 shows two reservoirs of different temperatures. The engine with less efficiency is being driven as a heat pump and hence it is a reversible engine. If the less efficient engine is not reversible, then the device could be built, but the expressions for work and heat flow would not be valid.
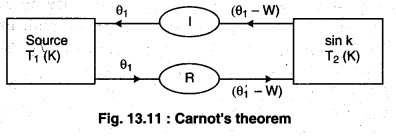
If one of the engines is irreversible, it must be the engine (I), placed so that it reverse drives the less efficient but reversible engine (R). But if the irreversible engine is more efficient than the reversible engine, then the second law of Thermodynamics is violated.
Efficiency of irreversible engine (ηI)
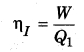
If the reversible engine takes the heat Q’1 from the source at temperature T1 and does work W and provides heat (Q’1 – W) to the sink. Then, the efficiency of reversible process (ηR),
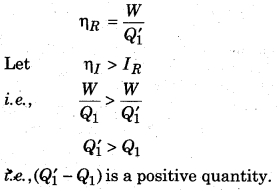
According to figure 13.11, both the engines are connected so that the irreversible engine does work in the same direction and the reversible engine performs work in the opposite direction, then the reversible engine does the work as the refrigerator (working on irreversible engine). The temperature T2 takes the heat (Q’1 – W) from the sink and work W is done on it. Here at temperature T1 it gives Q’1 heat to the source. Work done (W) on the reversible engine is fulfilled by the irreversible engine; and irreversible engine and refrigerators works as an automated device.
Since, the source provides Q1 heat to the irreversible engine and takes Q’1 heat from the reversible engine. Then,
Heat taken by the source = Q’1 – Q1
Similarly, the sink takes (Q1 – W) heat from the irreversible engine and gives (Q’1 – W) heat to the reversible engine. Then, loss in heat by the sink,
= (Q’1 – W) – (Q1 – W) = Q’1 – Q1
Since, Q’1 > Q1
∴ It is a positive quantity.
This means that the automated device, in every cycle, is transferring (Q’1 – Q1) heat from sink at T2 (low temperature) to the source at T1 (high temperature), which is not possible as second law of thermodynamics, i.e., our assumption ηI > ηR is not possible. Therefore, we can say that of all the engines working between similar temperature, reversible engines have maximum efficiency.
For the second statement of Carnot’s theorem, we replace the irreversible engine with another reversible engine (R’), i.e., two reversible engines are working between similar temperatures T1 (High) and T2 (low). Now, if we consider the efficiency of R engine (ηR) to be greater than that of engine R’ (ηR’)-
Then, the result again violates the second law of Thermodynamics. This implies the transfer of heat from low temperature to high temperature without heat loss. Therefore ηR > ηR, then the result is same and violation is obtained, i. e., it must be ηR = ηR’. So, we can say that all the reversible engines working at similar temperatures will have similar efficiency.
Refrigerator : A refrigerator is a carnet’s heat engine working in the reverse direction.
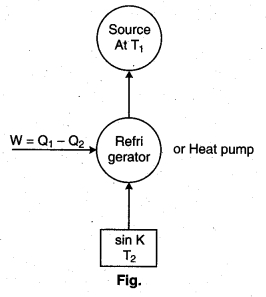
In a refrigerator or heat pump, the working substance absorbs an amount of heat O12 from the sink at temperature (T2). An amount of work W is done on it by the external agency and rejects a larger quantity of heat to the source at temp T1.
Coefficient of performance : It may be defined as the ratio of the amount of heat removed (Q2) percycle to the mechanical work (W) required to be done on it :
RBSE Class 11 Physics Chapter 13 Numerical Questions
Question 1.
The efficiency of an ideal engine is 75% and it emits heat 2 × 103 W to sink at 283 K, then calculate :
(i) Temperature of source.
(ii) Work done per minute by the engine.
(iii) Absorbed heat from the source in a cycle.
Solution:

Question 2.
Calculate the efficiency of a Carnot engine working between freezing point and boiling point.
Solution:
Given, T1 = 100°C = 100 + 273 = 373K;
T2 = 0°C = 273K

Question 3.
The efficiency of a Carnot engine is 40%. If the temperature of the source is 193.6°C, then determine the temperature of the sink.
Solution:
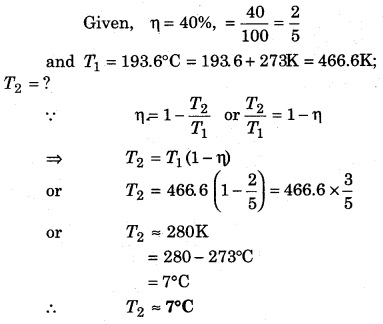
Question 4.
A Carnot refrigerator is operated between 260 K and 400 K. It takes 600 cal heat from sink at low temperature, then calculate the heat given to source at high temperature and the work in every cycle.
Solution:
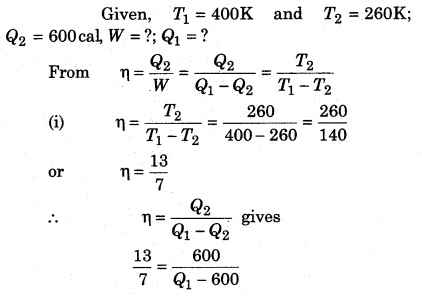

Question 5.
The efficiency of a Carnot engine at temperature 100 K and T K; and 180 K and 900 K is same, then calculate T.
Solution:
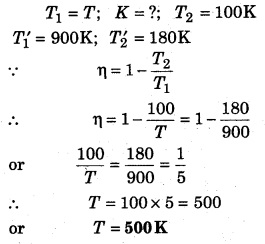
Question 6.
Two Carnot engines A and B are working in series. First engine A takes heat at 900 K and gives heat to the sink at T K. Another engine B, takes the heat from A and emits it to sink at 400 K. Calculate the temperature T in following conditions :
(i) when same work is done by both the engines.
(ii) when efficiency of both the engines is equal.
Solution:
(i) When same work is done by both the engines,
Let’s assume that engine A takes heat Q1 from the source and gives heat Q2 to the sink, then
Carnot cycle
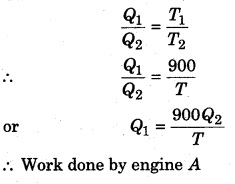
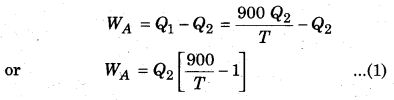
Now, lets assume engine Stakes heat Q2 from its source (at temperature T) and gives away Q3 to its sink (at temperature T = 400K). Then again from Carnot’s cycle.
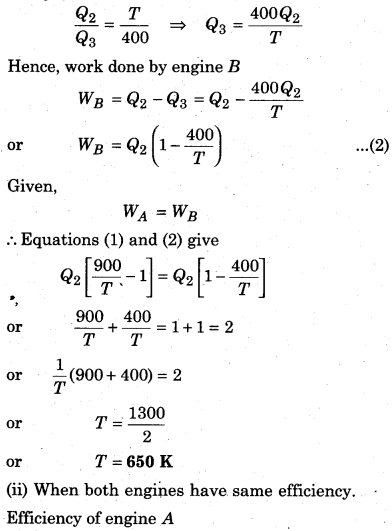
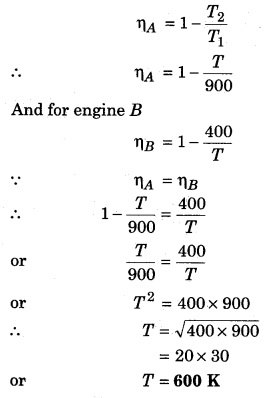
Question 7.
A gas (γ = 1.5) is compressed in an adiabatic process, then its volume changes from 1600 cm3 to 400 cm3. If the initial pressure is 150 kPa, then calculate the final pressure, and the work done on the gas.
Solution:
Given, γ = 1.5;
V1 = 1600 cm3 = 1600 × 10-6 m3 = 1.6 × 10-3 m3;
V2 = 400 cm3 = 400 × 10-6 m3 = 0.4 × 10-3 m3;
P1 = 150kPa
or P1 = 150 × 103 Pa = 1.5 × 105 Pa; P2 = ?
∵ In an adiabatic process
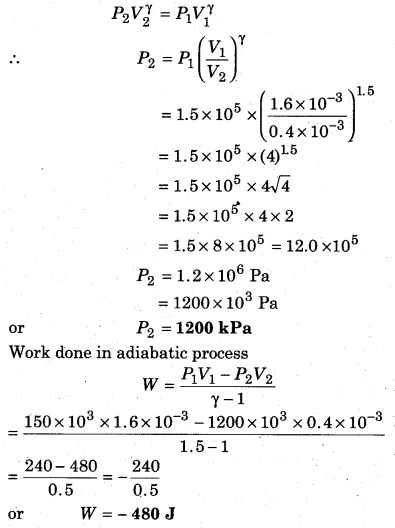
Question 8.
If a gas (γ = 1.5) is compressed at pressure 27 times the initial pressure, then calculate the change in temperature if the initial temperature is 27°C.
Solution:
Given, γ = 1.5; P1 = P; P2 = 27P;
T1 = 27 + 273 = 300K; T2 = ?
∴ Relation between pressure and temperature in an adiabatic process
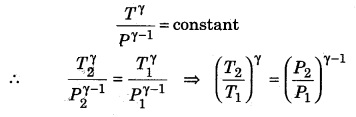
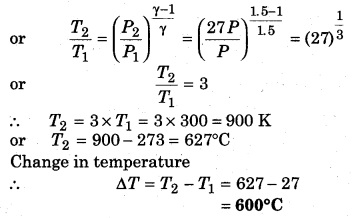
Question 9.
A refrigerator transfers 200 J average heat per second from temperature -10°C to 27°C. Taking the cycle to be reversible, calculate the average power when there is no loss of heat.
Solution:

Question 10.
P-V curve of a cyclic process is shown below, then calculate the work done in the cyclic process.
Solution:
The given cyclic process is anticlockwise, hence work done will be positive.
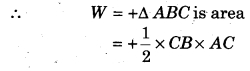
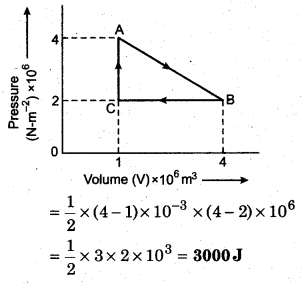
Question 11.
A Carnot engine operates between 373K and 283 K. Then, calculate the efficiency and deduce that when would its efficiency be 100%.
Solution:
