Rajasthan Board RBSE Class 11 Physics Chapter 4 गति के नियम
RBSE Class 11 Physics Chapter 4 पाठ्य पुस्तक के प्रश्न एवं उत्तर
RBSE Class 11 Physics Chapter 4 अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
किसी वस्तु पर यदि नेट बल शून्य है तो उसका त्वरण क्या होगा?
उत्तर:
शून्य
प्रश्न 2.
किसी वस्तु के संवेग का सूत्र लिखिये।
उत्तर:
\(\overrightarrow{\mathrm{P}}=m \vec{v}\)
प्रश्न 3.
न्यूटन का गति का द्वितीय नियम सूत्र रूप में लिखिए।
उत्तर:
\(\overrightarrow{\mathrm{F}}=\frac{d \overrightarrow{\mathrm{P}}}{d t}=m \vec{a}\)
प्रश्न 4.
न्यूटन के गति के तृतीय नियम में क्रिया एवं प्रतिक्रिया की दिशा क्या होती है ?
उत्तर:
परस्पर विपरीत
प्रश्न 5.
परिवर्ती द्रव्यमान वाले तंत्र का एक उदाहरण दीजिए।
उत्तर:
रॉकेट।
प्रश्न 6.
किसी दो सम्पर्कित पृष्ठों के मध्य स्थैतिक एवं गतिज घर्षण में से किसका मान अधिक होता है?
उत्तर:
स्थैतिक
प्रश्न 7.
µs एवं µk में किसका मान अधिक होता है ?
उत्तर:
µ<subs
प्रश्न 8.
एक समान वृत्तीय गति में कौन-सा बल विद्यमान होता है?
उत्तर”
अभिकेन्द्रीय
प्रश्न 9.
समतल वृत्ताकार पथ पर एक वाहन को आवश्यक अभिकेन्द्रीय बल कैसे प्राप्त होता है?
उत्तर:
घर्षण बल द्वारा।
प्रश्न 10.
एक बंकित वृत्ताकार पथ पर घर्षण बल के अलावा आवश्यक अभिकेन्द्रीय बल कैसे प्राप्त होता है?
उत्तर:
अभिलम्ब बल के घटक द्वारा
RBSE Class 11 Physics Chapter 4 लघूत्तरात्मक प्रश्न
प्रश्न 1.
स्पष्ट कीजिए कि क्यों किसी तीव्र गति से चल रही बस के यकायक रुकने पर यात्री आगे की ओर गिरते हैं?
उत्तर:
जब किसी तीव्र गति से चल रही बस को रोकने के लिए यकायक ब्रेक लगाया जाता है तो हमारे शरीर का नीचे वाला भाग जो बस के सम्पर्क में है, वह बस के साथ रुक जाता है, परन्तु शरीर का ऊपरी भाग जड़त्व के कारण एक समान वेग से आगे की ओर गतिशील रहना चाहता है। अतः यह आगे की ओर एक धक्के का अनुभव करता है।
प्रश्न 2.
न्यूटन के गति के प्रथम नियम को जड़त्व का नियम क्यों कहते हैं?
उत्तर:
‘यदि कोई वस्तु विरामावस्था में है तो विरामावस्था में ही रहेगी और यदि गतिमान अवस्था में है तो गतिमान अवस्था में ही रहेगी जब तक कि उस पर कोई बाह्य बल ने लगाया जाये।”
बाह्य बल के अभाव में किसी वस्तु में अपनी विरामावस्था अथवा एकसमान गति अवस्था को बनाये रखने की प्रवृत्ति होती है। अर्थात् प्रत्येक वस्तु में उसकी वर्तमान अवस्था में परिवर्तन के विरोध का गुण होता है। यही गुण जड़त्व कहलाता है। इसलिए न्यूटन के गति का प्रथम नियम जड़त्व का नियम भी कहलाता है।
प्रश्न 3.
क्रिकेट का खिलाड़ी गेंद को लपकते समय अपने हाथ गेंद के साथ पीछे की ओर क्यों खींचता है?
उत्तर:
क्रिकेट का कोई खिलाड़ी जब तीव्र गति से आती हुई गेंद को पकड़ता है तब वह अपने हाथ पीछे की ओर खींचता है। इसका कारण यह है कि प्रारम्भ में गेंद गतिशील है तथा खिलाड़ी हाथों से गेंद को रोकने के लिए मंदक बल लगाता है। अब यदि खिलाड़ी गेंद को अचानक पकड़ ले तब गेंद का मंदन बहुत अधिक होने से गेंद को रोकने के लिए बहुत अधिक बल लगाना पड़ेगा, जिससे खिलाड़ी की हथेली में चोट लग सकती है। जब खिलाड़ी अपने हाथ को पीछे की ओर ले जाकर गेंद को धीरे से पकड़े तब मंदन कम होगा अतः खिलाड़ी को गेंद पकड़ने में कम बल लगाना पड़ेगा और खिलाड़ी की । हथेली में चोट लगने की सम्भावना नहीं रहेगी।
प्रश्न 4.
बल की परिभाषा दीजिए।
उत्तर:
बल (Force)- किसी स्थिर वस्तु को गतिशील करने । के लिए प्रयास के रूप में धक्का देना या खींचना अथवा गतिशील वस्तु को रोकने या उसके वेग में परिवर्तन के लिए वस्तु को खींचना बल कहलाता है। दूसरे शब्दों में, इस प्रकार कहा जा सकता है कि बल वह भौतिक राशि है जो किसी वस्तु क़ी यांत्रिक स्थिति में परिवर्तन कर सकता है। यह एक सदिश राशि है। इसे हम F से प्रदर्शित करते हैं।
“किसी वस्तु पर लगने वाला बल F वस्तु के द्रव्यमान in तथा उसमें उत्पन्न त्वरण 4 के गुणनफल के अनुक्रमानुपाती होता है।”
S.I. पद्धति में बल का व्यावहारिक मात्रक ‘न्यूटन’ है।
प्रश्न 5.
एक जड़त्वीय तंत्र के अन्तर्गत एक कण का त्वरण मापने पर शून्य आता है। क्या हम कह सकते हैं कि कण पर कोई बल कार्यरत नहीं है? स्पष्ट करिए।
उत्तर:
हाँ, कण पर कोई बल कार्यरत नहीं है। चूंकि इस स्थिति में कण या तो स्थिर रहता है अथवा एकसमान वेग से रेखीय गति करता है। (जड़त्व का नियम) अतः इन्हें जड़त्वीय निर्देश तंत्र कहा जाता है।
प्रश्न 6.
न्यूटन के गति के तृतीय नियम के अनुसार रस्साकशी के खेल में प्रत्येक टीम अपनी विरोधी टीम को समान बल से खींचती है। तो फिर एक टीम जीतती है और दूसरी हार जाती है, ऐसा क्यों?
उत्तर:
क्रिया एवं प्रतिक्रिया बल परिमाण में बराबर परन्तु विपरीत होते हैं। लेकिन, वे दो अलग वस्तुओं पर कार्य करने के कारण एक-दूसरे को निरस्त नहीं कर पाते हैं।
प्रश्न 7.
एक मेज पर एक किताब रखी हुई है। किताब का भार एवं मेज द्वारा किताब पर लगाया गया अभिलम्ब बल परिमाण में समान एवं दिशा में विपरीत है। क्या इसे न्यूटन के तृतीय नियम का उदाहरण माना जा सकता है? स्पष्ट करिए।
उत्तर:
हाँ, किसी मेज पर एक पुस्तक रखी है, जैसा चित्र (i) में दिखाया गया है। पुस्तक का भार W नीचे की ओर मेज पर लगता। है। मेज द्वारा पुस्तक पर प्रतिक्रिया बले R ऊपर की ओर लगता है। न्यूटन के तृतीय नियमानुसार
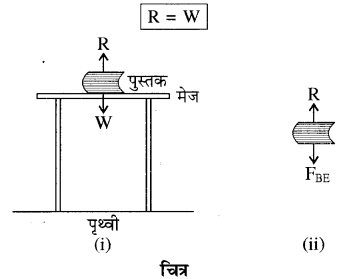
चित्र (ii) में मेज पर रखी पुस्तक पर लग रहे सभी बल दिखाये गये हैं। FBE पुस्तक पर पृथ्वी के गुरुत्वाकर्षण द्वारा लग रहा बल है। यद्यपि FBE भार के बराबर है लेकिन R और FBE क्रिया-प्रतिक्रिया वाले तीसरे नियम के युग्म नहीं हैं। चित्रे (ii) में पुस्तक पर लगने वाला परिणामी बल शून्य है और पुस्तक स्थिर अवस्था में रहती है।
प्रश्न 8.
किसी वस्तु पर लगने वाले आवेग की परिभाषा लिखिए।
उत्तर:
पिण्ड पर आरोपित बल एवं जितने समय के लिए वह कार्यरत रहता है, उनके गुणनफल को आवेग कहते हैं। यह एक सदिश राशि है। इसको \(\overrightarrow{\mathrm{J}}\) से प्रदर्शित किया जाता है।
किसी पिण्ड पर कोई बल \(\overrightarrow{\mathrm{F}}\) अल्प समय dt के लिए लगाया जाता है, तो इस बल का आवेग होगा
\(d \overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{F}} d t\)
इसका मात्रक न्यूटन सेकण्ड होता है।
प्रश्न 9.
आवेगी बल क्या होते हैं?
उत्तर:
क्रिकेट के मैच में बैट द्वारा बॉल पर लगाया गया अत्यधिक बल जो बहुत कम समय के लिए (टक्कर के समय) लगाया जाता है। इस प्रकार के अत्यधिक बल जो अत्यल्प अवधि (स्पर्श काल) के लिए कार्यरत होते हैं, आवेगी बल कहलाते हैं। यह आवश्यक नहीं है कि स्पर्शकाल में ये बल एकसमान हों
प्रश्न 10.
आवेग-संवेग प्रमेय को लिखिए।
उत्तर:
\(\overrightarrow{\mathrm{J}}=\overrightarrow{\mathrm{P}_{2}}-\overrightarrow{\mathrm{P}_{1}}\)
किसी बल का आवेग उस बल के कारण संवेग में परिवर्तन के बराबर होता है, इसे आवेग-संवेग का प्रमेय कहते हैं। इस प्रमेय के अनुसार यदि संवेग में परिवर्तन नियत होता है तो उसका आवेग भी नियत होगा।
प्रश्न 11.
संवेग संरक्षण का नियम लिखिए।
उत्तर:
न्यूटन के द्वितीय नियम के अनुसार यदि किसी वस्तु या निकाय पर कुल बाह्य बल \(\overrightarrow{\mathrm{F}}\) लग रहा है, तब उसके परिवर्तन की दर निम्न होती है
\(\frac{d \overrightarrow{\mathrm{P}}}{d t}=\overrightarrow{\mathrm{F}}\)
यदि निकाय पर कुल बाह्य बल शून्य है, तब
\(\frac{d \overrightarrow{\mathrm{P}}}{d t}\) = 0 या \(\overrightarrow{\mathrm{P}}\) = नियतांक
अतः यदि किसी निकाय या वस्तु पर कुल बाह्य बल शून्य होता है, तब उस निकाय का संवेग, परिमाण व दिशा में अपरिवर्तित रहता है। इसे संवेग संरक्षण या रैखिक संवेग संरक्षण का नियम कहते हैं।
प्रश्न 12.
विलगित निकाय किसे कहते हैं?
उत्तर:
ऐसा निकाय जिस पर कोई बाह्य बल कार्य नहीं कर रहा है या कार्यरत बाह्य बलों का सदिश योग शून्य है, एक विलगित या वियुक्त निकाय कहलाता है। एक विलगित निकाय की कुल संवेग नियत या संरक्षित रहता है।
प्रश्न 13.
किसी बन्दूक से एक गोली छोड़ने पर बन्दूक पीछे की ओर प्रतिक्षिप्त क्यों करती है?
उत्तर:
इसका कारण यह है कि प्रारम्भ में बन्दूक और गोली विरामावस्था में होते हैं। अतः सम्पूर्ण निकाय का संवेग शून्य होता है। जब बन्दूक दागी जाती है तो बन्दूक आगे की दिशा में गोली के संवेग की क्षतिपूर्ति के लिए पीछे की ओर प्रतिक्षिप्त करती है।
प्रश्न 14.
घर्षण कितने प्रकार के होते हैं?
उत्तर:
सामान्य रूप से घर्षण को दो प्रकारों में विभाजित कर सकते हैं
- स्थैतिक घर्षण (Static Friction)
- सप अथवा गतिज घर्षण (Kinetic Friction)
प्रश्न 15.
अभिकेन्द्रीय त्वरण को परिभाषित करिए।
उत्तर:
अभिकेन्द्रीय त्वरण ar = \(\frac{v^{2}}{r}\) होता है।
r त्रिज्या के एक वृत्ताकार पथ में नियत चाल से गति कर रहे। कण का स्पर्श रेखीय त्वरण शून्य और अभिकेन्द्रीय त्वरण \(\frac{v^{2}}{r}\) होता है। ऐसे कण का कुल त्वरण भी \(\frac{v^{2}}{r}\) ही होता है।
a = \(\sqrt{a_{\mathrm{T}}^{2}+a_{r}^{2}}=\sqrt{0+a_{r}^{2}}\) = ar
a = ar ∴ a = \(\frac{v^{2}}{r}\)
प्रश्न 16.
किसी वृत्ताकार मोड़ पर एक सड़क को बंकित क्यों किया जाता है?
उत्तर:
हम जानते हैं Vmax = \(\sqrt{\mu r g}\)
यदि एक कार की गति सड़क के वृत्ताकार मोड़ पर उपरोक्त द्वारा दिये गये मान से अधिक है तो कार वृत्ताकार मोड़ के केन्द्र के बाहर की ओर लुढ़क (skid) या गिर जायेगी। इस समस्या के निदान हेतु हम सड़क को बाहर के किनारे से थोड़ा ऊपर उठा देते हैं, ताकि गति के लिए आवश्यक अभिकेन्द्रीय बल केवल घर्षण बल द्वारा ही प्राप्त न होकर अभिलम्ब बल के एक घटक द्वारा प्राप्त हो । इस प्रकार की सड़क को बंकित सड़क (Banked road) कहते हैं।
प्रश्न 17.
जड़त्वीय निर्देश तंत्र को परिभाषित करिए।
उत्तर:
ऐसे निर्देश तंत्र जिनमें न्यूटन के गति सम्बन्धी प्रथम और द्वितीय नियम वैध होते हैं, जड़त्वीय निर्देश तंत्र कहलाते हैं। इस प्रकार के तंत्र में यदि किसी कण पर कोई बाह्य बल कार्यकारी नहीं है। तो यह कण या तो स्थिर रहता है अथवा एकसमान वेग से सरल रेखीय गति करता है (जड़त्व का नियम) अतः इन्हें जड़त्वीय निर्देश तंत्र कहा जाता है।
प्रश्न 18.
अजड़त्वीय निर्देश तंत्र को परिभाषित करिए।
उत्तर:
वे निर्देश तंत्र जिनमें न्यूटन के गति सम्बन्धी प्रथम दो नियम वैध नहीं रहते, अजड़त्वीय निर्देश तंत्र कहलाते हैं। इन तंत्रों में बल की अनुपस्थिति में भी किसी कण की गति त्वरित प्रतीत होती है। सभी त्वरित तंत्र एवं घूर्णन करते हुए तंत्र अजड़त्वीय होते हैं।
प्रश्न 19.
क्या पृथ्वी जड़त्वीय निर्देश तंत्र है?
उत्तर:
पृथ्वी जड़त्वीय निर्देश तंत्र नहीं है क्योंकि पृथ्वी न केवल अपनी स्वयं की अक्ष पर अपितु सूर्य के चारों ओर भी घूर्णन करती है। पृथ्वी की स्वयं की घूर्णन गति के कारण इसकी सतह पर रखा कोई स्थिर कण इसके केन्द्र की ओर अभिकेन्द्रीय बल का अनुभव करता है। उदाहरणतः भूमध्य रेखा पर इस अभिकेन्द्रीय त्वरण का मान
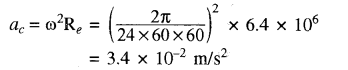
सामान्य यांत्रिकी की समस्याओं में इस त्वरण को यदि न्यून मान कर छोड़ दें तो पृथ्वी को जड़त्वीय निर्देश तंत्र माना जा सकता है परन्तु कतिपय समस्याओं में, इस त्वरण के प्रभाव दृष्टिगोचर होते हैं।
RBSE Class 11 Physics Chapter 4 निबन्धात्मक प्रश्न
प्रश्न 1.
न्यूटन के गति का द्वितीय नियम क्या है? इसे परिभाषित करिए। इससे गति के प्रथम नियम को व्युत्पन्न करिये।
उत्तर:
न्यूटन का गति का द्वितीय नियम (Newton’s Second Law of Motion)
न्यूटन के गति के द्वितीय नियम के अनुसार किसी वस्तु के रेखीय संवेग में परिवर्तन की दर वस्तु पर आरोपित बाह्य बल के समानुपाती होती है। वस्तु के रेखीय संवेग में यह परिवर्तन कार्यरत बल के कारण कार्यरत बल की दिशा में होता है।” अर्थात्
\(\overrightarrow{\mathrm{F}} \propto \frac{\overrightarrow{d \mathrm{P}}}{d t}\)
या \(\overrightarrow{\mathbf{F}}=\frac{\mathrm{K} \overrightarrow{d \mathrm{P}}}{d t}\) …………(1)
यहाँ पर K समानुपाती नियतांक है जिसका मान चयनित मात्रकों पर निर्भर करता है। मात्रकों का चयन इस प्रकार से करते हैं कि K का मान 1 प्राप्त हो जाये।
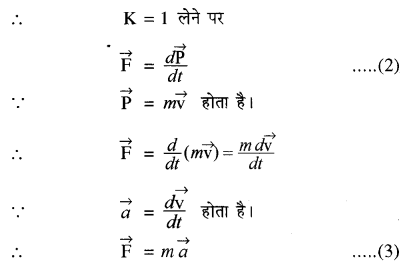
अर्थात् किसी वस्तु पर लगाया गया नेट बल उस वस्तु के द्रव्यमान और वस्तु के त्वरण के गुणनफल के बराबर होता है। बल लगाने पर वस्तु में उत्पन्न त्वरण, बल की दिशा में उत्पन्न होता है। वस्तुतः न्यूटन का प्रथम नियम बल की परिभाषा देता है, जबकि न्यूटन का द्वितीय नियम बल का परिमाण निर्धारित करता है। समीकरण (3) से स्पष्ट है कि एकांक द्रव्यमान वाली वस्तु में एकांक त्वरण उत्पन्न करने वाले बल का परिमाण इकाई बल के तुल्य होता है।
समीकरण (3) से यदि \(\vec{F}\) = 0 तो \(\vec{a}\) = 0 यह गति का प्रथम नियम है। अतः प्रत्यक्ष रूप से द्वितीय नियम प्रथम नियम के अनुरूप है।
न्यूटन बल की परिभाषा- यदि कोई बल, 1 किग्रा. की वस्तु में 1 मी./से.2 का त्वरण उत्पन्न कर दे तब वह बल 1 न्यूटन बल के बराबर होता है।
1 न्यूटन = (1 किग्रा.) × (1 मी./से.2)
या 1N = 1 Kg m/s2
बल की विमा [MLT-2] है। अन्तर्राष्ट्रीय पद्धति में मात्रक न्यूटन के अलावा बल के अन्य मात्रक डाइन (dyne, CGS मात्रक पद्धति में) और पाउण्डल (FPS मात्रक पद्धति में) होते हैं, पर इनका उपयोग अब नहीं करना चाहिए।
भार (Weight)- किसी वस्तु का भार उस वस्तु पर लग रहे गुरुत्वाकर्षण बल के बराबर होता है। यदि वस्तु का द्रव्यमान m तथा गुरुत्व जनित त्वरण g है, तब वस्तु का भार,
W = mg
होता है। भार का मात्रक न्यूटन तथा विमा [MLT-2] है। कई बार सुविधा की दृष्टि से भार को किग्रा. भार में व्यक्त किया जाता है। 1 किग्रा. भार, एक किलोग्राम द्रव्यमान के भार के बराबर होता है, अर्थात्
1 किग्रा. भार = 1 किग्रा. × g (मी./से.2) .
या 1 किग्रा. भार = g न्यूटन = 9.8 न्यूटन
न्यूटन की गति के द्वितीय नियम के उदाहरण
(i) क्रिकेट का कोई खिलाड़ी जब तीव्र गति से आती हुई गेंद को पकड़ता है तब वह अपने हाथ पीछे की ओर खींचता है। इसका कारण यह है कि प्रारम्भ में गेंद गतिशील है तथा खिलाड़ी हाथों से गेंद को रोकने के लिए मंदक बल लगाता है। अब यदि खिलाड़ी गेंद को अचानक पकड़ ले तब गेंद का मंदन बहुत अधिक होने से गेंद को रोकने के लिए बहुत अधिक बल लगाना पड़ेगा, जिससे खिलाड़ी की हथेली में चोट लग सकती है। जब खिलाड़ी अपने हाथ को पीछे की ओर ले जाकर गेंद को धीरे से पकड़े तब मंदन कम होगा अतः खिलाड़ी को गेंद पकड़ने में कम बल लगाना पड़ेगा और खिलाड़ी की हथेली में चोट लगने की सम्भावना नहीं रहेगी।
(ii) जब कोई व्यक्ति किसी ऊँचाई से कठोर फर्श पर कूदता है। तब व्यक्ति का वेग तुरन्त ही शून्य हो जाता है और व्यक्ति पर फर्श द्वारा आरोपित बल अत्यधिक होता है जिसके कारण व्यक्ति को चोट लग सकती है। इसके विपरीत यदि व्यक्ति समान ऊँचाई से रेत में कूदता है। तब उसके पैर रेत में धंसने से उसके वेग में परिवर्तन धीरे-धीरे होता है। जिससे फर्श द्वारा आरोपित बल कम होने से व्यक्ति को चोट नहीं लगती है।
प्रश्न 2.
न्यूटन के गति का तृतीय नियम परिभाषित कीजिए इसे दो उदाहरणों द्वारा समझाइये।
उत्तर:
इस नियम के अनुसार प्रत्येक क्रिया की, परिमाण में समान परन्तु दिशा में विपरीत प्रतिक्रिया उत्पन्न होती है। इसे क्रिया-प्रतिक्रिया का नियम भी कहते हैं। प्रथम वस्तु द्वारा द्वितीय वस्तु पर लगाया गया बल क्रिया कहलाता है और द्वितीय वस्तु द्वारा प्रथम वस्तु पर लगाया गया बल प्रतिक्रिया कहलाता है। इस नियम को गणितीय रूप में निम्न प्रकार व्यक्त कर सकते हैं
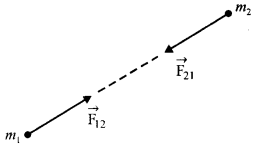
\(\overrightarrow{\mathrm{F}_{21}}=-\overrightarrow{\mathrm{F}_{12}}\) ………… (1)
यहाँ पर \(\overrightarrow{\mathrm{F}_{12}}\) (प्रतिक्रिया) प्रथम वस्तु पर द्वितीय वस्तु द्वारा लगाया गया बल तथा \(\overrightarrow{\mathrm{F}_{21}}\) (क्रिया) द्वितीय वस्तु पर प्रथम वस्तु द्वारा लगाया गया बल है। यहाँ पर ऋणात्मक चिन्ह विपरीत दिशा को प्रदर्शित करता है। इन दोनों बलों में से एक को क्रिया एवं दूसरे को प्रतिक्रिया बल कहते हैं। इस नियम के महत्त्वपूर्ण तथ्य निम्नलिखित
- किसी भी साधन द्वारा लगाया गया बल क्रिया तथा उसके कारण अनुभव किया गया बल प्रतिक्रिया बल कहलाता है।
- यह निश्चित तौर पर नहीं कहा जा सकता कि कौनसा क्रिया बल है तथा कौनसा उसका प्रतिक्रिया बल है। केवल यह कहा जा सकता है कि इन दोनों बलों में से एक क्रिया बल है और दूसरा इसका प्रतिक्रिया बल है।
- क्रिया एवं प्रतिक्रिया बलों की उत्पत्ति दोनों वस्तुओं के सम्पर्कित होने पर अथवा उनके दूर रहने पर भी सम्भव है।
- क्रिया एवं प्रतिक्रिया बल सदैव अलग-अलग पिण्डों पर लगते हैं, एक पिण्ड पर नहीं, इसी कारण ये एक-दूसरे के प्रभाव को समाप्त नहीं करते और प्रत्येक बल अपना-अपना प्रभाव उत्पन्न करता है।
- क्रिया और प्रतिक्रिया का नियम वस्तु के स्थिर अथवा | गतिशील दोनों स्थितियों में लागू होता है।
- क्रिया एवं प्रतिक्रिया का नियम सभी प्रकार के बलों जैसे | गुरुत्वीय, वैद्युत, चुम्बकीय बल आदि में लागू होता है।
उदाहरणार्थ-
- एक तैराक जब अपने हाथों से पानी को पीछे धकेल कर क्रिया करता है तो धकेला हुआ पानी तैराक को उतनी ही प्रतिक्रिया से आगे की ओर धकेल देता है।
- जब बन्दूक चलाई जाती है, तो गोली जिस बल से आगे बढ़ती है ( क्रिया) बन्दूक पर उतना ही बल पीछे की ओर ( प्रतिक्रिया) लगता है।
- नाव खेने वाला व्यक्ति जितनी क्रिया से पानी को पीछे धकेलता है उतनी ही प्रतिक्रिया से पानी, नाव को आगे बढ़ने के लिए आवश्यक प्रतिक्रिया बल प्रदान करता है।
- किसी धरातल पर स्थित पिण्ड का भार (क्रिया बल ) नीचे की ओर लगता है, जबकि धरातल द्वारा प्रतिक्रिया बल R पिण्ड पर ऊपर की ओर लगता है।
- जब कोई व्यक्ति पृथ्वी पर पैदल चलता है तो वह पैर के पंजों के द्वारा तिर्यक बल F से पृथ्वी को पीछे की ओर दबाता है। (क्रिया) पृथ्वी भी उतना ही बल (प्रतिक्रिया) विपरीत दिशा में लगाती है। इस प्रतिक्रिया बल को दो समकोणिक घटकों में वियोजित किया जा सकता है। क्षैतिज घटक व्यक्ति को आगे बढ़ने में मदद करता है जबकि ऊर्ध्वाधर घटक व्यक्ति के भार को सन्तुलित करता है।
प्रश्न 3.
आवेग-संवेग प्रमेय को लिखिए तथा इसे सिद्ध कीजिए। ग्राफीय विधि से आवेग का मान कैसे ज्ञात करेंगे?
उत्तर:
आवेग-पिण्ड पर आरोपित बल एवं जितने समय के लिये वह कार्यरत रहता है, उनके गुणनफल को आवेग कहते हैं। यह एक सदिश राशि है, इसको \(\overrightarrow{\mathrm{J}}\) से प्रदर्शित किया जाता है।
किसी पिण्ड पर कोई बल \(\overrightarrow{\mathrm{F}}\) अल्प समय dt के लिये लगाया जाता है तो इस पर बल का आवेग होगा
\(d \vec{J}=\overrightarrow{\mathrm{F}} d t\) ………….. (1)
यदि बल निश्चित समय अन्तराल t1 से t2 तक कार्यरत रहता है। तो बल F का आवेग समीकरण (1) का समाकलन करने पर ज्ञात किया जा सकता है।
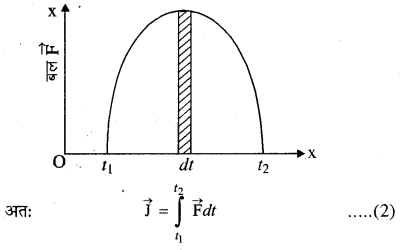
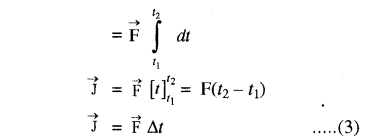
अतः नियत बल का निश्चित समय अन्तराल में आवेग बल तथा समय अन्तराल के गुणनफल के बराबर होता है। इसका मात्रक न्यूटन सेकण्ड होता है।
न्यूटन के दूसरे नियम से
\(\overrightarrow{\mathrm{F}}=\frac{d \overrightarrow{\mathrm{P}}}{d t}\)
जहाँ किसी समय t पर पिण्ड का संवेग \(\overrightarrow{\mathrm{P}}_{1}\) तथा उस पर कार्यरत बल में है।
\(\overrightarrow{\mathrm{F}} d t=d \overrightarrow{\mathrm{P}}\)
यदि t1 समय पर पिण्ड क़ा संवेग हैं \(\overrightarrow{\mathrm{P}}_{1}\) और t1 समय पर उसका संवेग है, है तो
\(\int_{t_{1}}^{t_{2}} \overrightarrow{\mathrm{F}} d t=\int_{\mathrm{P}_{1}}^{\overrightarrow{\mathrm{P}}_{2}} d \overrightarrow{\mathrm{P}}\)
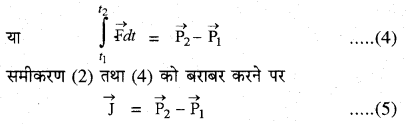
अतः किसी बल का आवेग उस बल के कारण संवेग में परिवर्तन के बराबर होता है, इसे आवेग-संवेग का प्रमेय कहते हैं। इस प्रमेय के अनुसार यदि संवेग में परिवर्तन नियत होता है तो उसका आवेग भी नियत होगा।
यदि किसी वस्तु पर \(\overrightarrow{\mathrm{F}}_{1}\) नियत बल के t1 समय तक लगने पर लगा आवेग और उसी वस्तु पर \(\overrightarrow{\mathrm{F}}_{2}\) नियत बल के t2 समय तक लगने पर लगा आवेग समान हों तब
\(\overrightarrow{\mathrm{F}}_{1} t_{1}=\overrightarrow{\mathrm{F}}_{2} t_{2}\) ………… (6)
एक नियत संवेग परिवर्तन को यदि कम समय में करना हो तब बल अधिक लगाना पड़ेगा और वह संवेग परिवर्तन अधिक समय में करना हो तब बल कम लगाना पड़ेगा।
उदाहरणार्थ-
- एक क्रिकेट खिलाड़ी तेज गति से आती बॉल को पकड़ने के लिये अपने हाथों को पीछे की ओर इसलिये करता है। ताकि संवेग में परिवर्तन में समय ज्यादा लगे और बल कम लगाना पड़े।
- एक व्यक्ति यदि रेत की तुलना में ठोस धरातल पर गिरता है तब उसे ज्यादा चोट लगने का खतरा रहता है क्योंकि संवेग में परिवर्तन में लगा समय रेत पर गिरने की तुलना में ठोस धरातल पर बहुत कम होता है, जिसके कारण ठोस धरातल के द्वारा शरीर पर लगने वाला बल अधिक होता है।
- तेज दौड़ने वाले धावक दौड़ समाप्त करने के बाद रुकने के लिए अपने वेग को धीरे-धीरे करके विराम में आते हैं, क्योंकि इससे रुकने का समय बढ़ जाता है तो उनके द्वारा महसूस किया जाने वाला बल घट जाता है।
प्रश्न 4.
किसी N कणों के निकाय के लिए संवेग संरक्षण का नियम लिखिए। न्यूटन के द्वितीय नियम का उपयोग करते हुए इसे व्युत्पन्न करिये। एक उदाहरण द्वारा संवेग संरक्षण के नियम को समझाइये।
उत्तर:
N कणों के निकाय के लिए संवेग संरक्षण का नियम
माना कि एक निकाय में N कण हैं और उनका सम्पूर्ण संवेग \(\overrightarrow{\mathrm{P}}\) है तो

ऐसा निकाय जिस पर कोई बाह्य बल कार्य नहीं कर रहा है या कार्यरत बाह्य बलों का सदिश योग शून्य है, एक विलगित या वियुक्त निकाय कहलाता है। समीकरण (7) के अनुसार एक विलगित निकाय का कुल संवेग नियत या संरक्षित रहता है। यह एक विलगित निकाय के लिए संवेग संरक्षण का नियम है।
समीकरण (7) एवं (8) के अनुसार निकाय के कण विशेष का संवेग या वेग परिवर्तित हो सकता है, परन्तु निकाय का सम्पूर्ण संवेग स्थिर ही रहेगा, जब तक निकाय पर कोई बाह्य बल आरोपित नहीं किया जाये।
संवेग संरक्षण के कई उदाहरण हैं। एक परिचित उदाहरण पर विचार करते हैं। किसी बन्दूक से एक गोली छोड़ी जाती है तो बन्दूक पीछे की ओर गति या प्रतिक्षिप्त (recoil) करती है। इसका कारण यह है कि प्रारम्भ में बन्दूक और गोली विरामावस्था में होते हैं। अतः सम्पूर्ण निकाय का संवेग शून्य होता है। जब बन्दूक दागी जाती है तो बन्दूक आगे की दिशा में गोली के संवेग की क्षतिपूर्ति (compensate) के लिए पीछे की ओर प्रतिक्षिप्त करती है। माना कि गोली का द्रव्यमान mb एवं वेग \(\vec{v}_{b}\) है तथा बन्दूक का द्रव्यमान mG तथा वेग \(\vec{v}_{\mathrm{G}}\) है तो संवेग संरक्षण नियम के अनुसार, क्योंकि प्रारम्भिक संवेग शून्य है, अतः
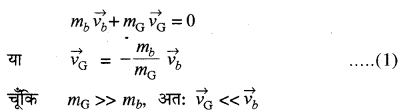
समीकरण (1) में ऋण चिह्न यह दर्शाता है कि गोली एवं बन्दूक के वेग परस्पर विपरीत दिशा में होते हैं।
रॉकेट की गति भी संवेग संरक्षण का बहुत अच्छा अनुप्रयोग प्रस्तुत करती है। इसका विस्तृत अध्ययन हम अगले अनुच्छेद में करेंगे।
न्यूटन के द्वितीय नियम के अनुसार यदि किसी वस्तु या निकाय पर कुल बाह्य बल \(\overrightarrow{\mathrm{F}}\) लग रहा है तब उसके परिवर्तन की दर निम्न होती है

अतः यदि किसी निकाय या वस्तु पर कुल बाह्य बल शून्य होता है तब उस निकाय का संवेग, परिमाण व दिशा में अपरिवर्तित रहता है। इसे संवेग संरक्षण या रैखिक संवेग संरक्षण का नियम कहते हैं।
माना दो परस्पर अन्योन्य क्रिया करने वाले कणों के द्रव्यमान m1 तथा m2 हैं तथा किसी क्षण इनके संवेग \(\overrightarrow{\mathrm{P}}_{1}, \overrightarrow{\mathrm{P}}_{2}\) हैं। और माना बाह्य बल क्रमशः \(\overrightarrow{\mathrm{F}}_{1}\) तथा \(\overrightarrow{\mathrm{F}}_{2}\) है। कणों की अन्योन्य क्रिया के कारण पहले का कण दूसरे कण के कारण लगने वाला बल \(\overrightarrow{\mathrm{F}}_{12}\) और दूसरे का कण पहले कण के कारण लगने वाला बल \(\overrightarrow{\mathrm{F}}_{21}\) है तब कण (1) पर कुल बल \(\left(\overrightarrow{\mathrm{F}}_{1}+\overrightarrow{\mathrm{F}}_{12}\right)\) और कण (2) पर कुल बल \(\left(\overrightarrow{\mathrm{F}}_{2}+\overrightarrow{\mathrm{F}}_{21}\right)\) होंगे। गति के द्वितीय नियम से (पहले कण के लिये)

अतः यदि किसी निकाय पर कुल बाह्य बल शून्य है तब उस निकाय का कुल संवेग नियत रहता है।
आन्तरिक बलों की उपस्थिति से इस नियम पर प्रभाव नहीं पड़ता चूँकि अन्योन्य क्रिया के कारण लगने वाले आन्तरिक बल न्यूटन के तृतीय नियम का पालन करते हैं।
प्रश्न 5.
रॉकेट की गति का वर्णन करिये तथा इसके वेग के लिए आवश्यक सूत्र ज्ञात कीजिए।
उत्तर:
रॉकेट की गति (Motion of a Rocket)- परिवर्ती द्रव्यमान एवं संवेग संरक्षण नियम का एक महत्त्वपूर्ण उदाहरण रॉकेट की गति का है। चूंकि रॉकेट में भरा हुआ ईंधन खर्च होता है, अतः रॉकेट का द्रव्यमान लगातार परिवर्तित होता है।
एक रॉकेट में, ईंधन के जलने के फलस्वरूप उच्च तापक्रम पर गैसें उत्पन्न होती हैं। ये गैसें रॉकेट के पीछे की ओर स्थिर एक चंचु (nozzle) से तीव्र गति से बाहर निकलती हैं। पीछे की ओर तीव्र गति से निकलने वाली गैस रॉकेट पर आगे की ओर एक बल लगाती है, जिसे रॉकेट का प्रणोद (thrust) कहते हैं और इसी के फलस्वरूप रॉकेट आगे की ओर त्वरित गति करता है। इसमें संवेग संरक्षण नियम का पालन होता है, जिसे नीचे चित्र में दर्शाया गया है
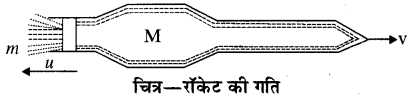
माना कि t = 0 पर रॉकेट का इसके ईंधन सहित द्रव्यमान M0 है। माना कि रॉकेट के पीछे से निष्कासित होने वाली गैसें, एक निश्चित दर r = \(\frac{d \mathbf{M}}{d t}\) से निकल रही हैं तथा इनका रॉकेट के सापेक्ष एक निश्चित वेग u है।
किसी क्षण है पर रॉकेट का अपने अन्दर बचे हुए ईंधन के साथ द्रव्यमान होगा। M = M0 – rt …………. (1)
यदि t समय पर रॉकेट का वेग y है तो इस द्रव्यमान M का संवेग होगा
P = Mv ………………… (2)
समीकरण (1) से M का मान रखने पर
P = (M0) – rt)v ……………. (3)
अब हम एक छोटे से समय अंतराल Δt पर विचार करें, तब इस समय अंतराल में द्रव्यमान ΔM = rΔt गैसों के रूप में रॉकेट से निष्कासित हो जाता है तथा रॉकेट का वेग v से बढ़कर v + Δv हो जाता है। गैसों का पृथ्वी के सापेक्ष वेग होगा
\(\vec{v}\) गैस, पृथ्वी = \(\vec{v}\) गैस, रॉकेट + \(\vec{v}\) रॉकेट, पृथ्वी
या v’ = – u + v = v – u
इसकी दिशा आगे की ओर (रॉकेट की गति की दिशा) होगी। (t + Δr) समय पर M द्रव्यमान का संवेग होगा।
(M – ΔM) (v + Δv) + ΔM (v – u) …………… (4)
यह मानते हुए कि ईंधन सहित रॉकेट निकाय पर कोई बाह्य बल कार्यरत नहीं है (यह उस स्थिति में है, जब रॉकेट पृथ्वी या अन्य किसी ग्रह के गुरुत्वीय क्षेत्र से बाहर है), संवेग संरक्षण के नियमानुसार समीकरण (3) एवं समीकरण (4) से।
(M – ΔM) (v + Δv) + ΔM(v – u) = Mv
या Mv + MΔv – ΔMv – ΔMΔV + ΔMv – ΔMu = Mv
या (M – ΔM) Δv = ΔMu

समीकरण (5) से रॉकेट के त्वरण का मान ज्ञात होता है। हम देखते हैं कि जैसे-जैसे समय निकलता जाता है, रॉकेट का त्वरण बढ़ता जाता है। यदि रॉकेट t = 0 पर अपनी गति प्रारम्भ करता है तथा हम किसी भी बाह्य बल यथा गुरुत्वीय बल आदि को नगण्य मान लें तो उपरोक्त समीकरण का समाकलन करने पर।
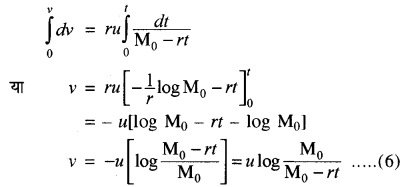
समीकरण (6) से हम किसी भी क्षण रॉकेट का वेग ज्ञात कर सकते हैं। इस समीकरण के अनुसार समय के बढ़ने के साथ रॉकेट को वेग बढ़ता जाता है।
प्रश्न 6.
घर्षण कितने प्रकार का होता है? उनके नियम लिखिए।
उत्तर:
घर्षण (Friction)-जब दो पिण्ड परस्पर स्पर्श करते हों तो। पिण्डों का वह गुण जिसके कारण उनके मध्यस्थ उनके स्पर्श बिन्दु पर एक स्पर्शीय प्रतिरोधी बल उत्पन्न होता है, जो एक पिण्ड को दूसरे पर सरकने या फिसलने से रोकता है, घर्षण (Friction) कहलाता है। और इस बल को घर्षण बल’ कहते हैं। ये दो प्रकार के होते हैं
- स्थैतिक घर्षण (Static Friction)
- गतिक घर्षण (Kinetic Friction)
प्रश्न 7.
स्थैतिक घर्षण की दिशा कैसे ज्ञात करेंगे? समझाइये।
उत्तर:
स्थैतिक घर्षण (Static Friction)
एक W भार के ब्लॉक को एक समतल पर रखा जाये और कोई बाह्य बल नहीं लगाया जाये तब सतह द्वारा ब्लॉक पर केवल प्रतिक्रिया बल R ही लगाया जाता है। ऐसी अवस्था में घर्षण बल उत्पन्न नहीं होता है, जिसे चित्र
(अ) में देखें अब हम यदि ब्लॉक पर बाह्य बल \(\overrightarrow{\mathrm{F}}\) लगाकर ब्लॉक को खिसकाने का प्रयास करें तो विपरीत दिशा में घर्षण बल उत्पन्न हो जाता है, जो आरोपित बल \(\overrightarrow{\mathrm{F}}\) को सन्तुलित कर देता है, जैसा चित्र
(ब) में दिखाया गया है। यहाँ पर ब्लॉक अब भी स्थैतिक अवस्था (स्थिर अवस्था, static) में ही रहता है। स्थैतिक अवस्था में उत्पन्न घर्षण बल \(\overrightarrow{f_{s}}\) को स्थैतिक घर्षण बल कहते हैं। जब आरोपित बल का मान एक सीमा से कम हो तब \(\overrightarrow{f_{s}}\) परिमाण में \(\overrightarrow{\mathrm{F}}\) के बराबर और दिशा में विपरीत लगता है। आरोपित बल \(\overrightarrow{\mathrm{F}}\) का मान बढ़ाने पर एक सीमा तक स्थैतिक घर्षण बल \(\left(\vec{f}_{s}\right)\) का मान भी बढ़ता है। जैसा चित्र
(स) में दिखाया गया है।
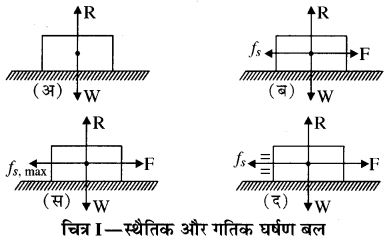
इस सीमा को fs, max कहें तब स्थैतिक घर्षण बल का यह मान सीमान्त घर्षण बल कहलाता है। प्रयोगों के आधार पर यह देखा गया है। कि दो सतहों के लिए।
fs, max ∝ R
यहाँ पर R ब्लॉक अर्थात् वस्तु पर लग रहा अभिलम्ब प्रतिक्रिया बल है। अतः
fs, max = µsR …………. (1)
जहाँ µs समानुपातिक नियतांक है और इसे स्थैतिक घर्षण गुणांक (coefficient of static friction) कहते हैं।
समीकरण (1) से µs = \(\frac{f_{s, \max }}{\mathrm{R}}\)
अर्थात् किन्हीं दो सतहों के मध्य स्थैतिक घर्षण गुणांक, सीमान्त घर्षण बल और अभिलम्ब प्रतिक्रिया बल के अनुपात के बराबर होता है। µs एक विमाहीन नम्बर है। इसका कोई भी मात्रक नहीं होता है।
प्रश्न 8.
स्थैतिक एवं गतिज घर्षण गुणांकों को परिभाषित कीजिए। इनका मान कैसे ज्ञात कर सकते हैं?
उत्तर:
स्थैतिक घर्षण (Static Friction)
एक W भार के ब्लॉक को एक समतल पर रखा जाये और कोई बाह्य बल नहीं लगाया जाये तब सतह द्वारा ब्लॉक पर केवल प्रतिक्रिया बल R ही लगाया जाता है। ऐसी अवस्था में घर्षण बल उत्पन्न नहीं होता है, जिसे चित्र (अ) में देखें अब हम यदि ब्लॉक पर बाह्य बल \(\overrightarrow{\mathrm{F}}\) लगाकर ब्लॉक को खिसकाने का प्रयास करें तो विपरीत दिशा में घर्षण बल उत्पन्न हो जाता है, जो आरोपित बल \(\overrightarrow{\mathrm{F}}\) को सन्तुलित कर देता है, जैसा चित्र
(ब) में दिखाया गया है। यहाँ पर ब्लॉक अब भी स्थैतिक अवस्था (स्थिर अवस्था, static) में ही रहता है। स्थैतिक अवस्था में उत्पन्न घर्षण बल \(\overrightarrow{f_{s}}\) को स्थैतिक घर्षण बल कहते हैं। जब आरोपित बल का मान एक सीमा से कम हो तब \(\overrightarrow{f_{s}}\) परिमाण में \(\overrightarrow{\mathrm{F}}\) के बराबर और दिशा में विपरीत लगता है। आरोपित बल \(\overrightarrow{\mathrm{F}}\) का मान बढ़ाने पर एक सीमा तक स्थैतिक घर्षण बल \(\left(\vec{f}_{s}\right)\) का मान भी बढ़ता है। जैसा चित्र
(स) में दिखाया गया है।
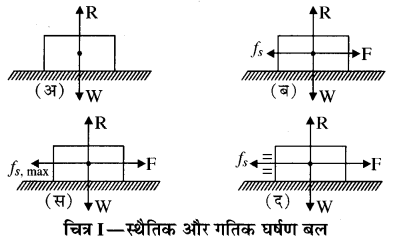
इस सीमा को fs, max कहें तब स्थैतिक घर्षण बल का यह मान सीमान्त घर्षण बल कहलाता है। प्रयोगों के आधार पर यह देखा गया है। कि दो सतहों के लिए।
fs, max ∝ R
यहाँ पर R ब्लॉक अर्थात् वस्तु पर लग रहा अभिलम्ब प्रतिक्रिया बल है। अतः
fs, max = µsR …………. (1)
जहाँ µs समानुपातिक नियतांक है और इसे स्थैतिक घर्षण गुणांक (coefficient of static friction) कहते हैं।
समीकरण (1) से µs = \(\frac{f_{s, \max }}{\mathrm{R}}\)
अर्थात् किन्हीं दो सतहों के मध्य स्थैतिक घर्षण गुणांक, सीमान्त घर्षण बल और अभिलम्ब प्रतिक्रिया बल के अनुपात के बराबर होता है। µs एक विमाहीन नम्बर है। इसका कोई भी मात्रक नहीं होता है।
गतिक घर्षण (Kinetic Friction)
यदि अभीष्ट वस्तु पर सम्पर्क बल के समानान्तर लगाये बल का मान स्थैतिक घर्षण बल के अधिकतम मान से अधिक है तो वस्तु, आरोपित बल की दिशा में फिसलने लगती है। वस्तु के फिसलने की स्थिति में गति की विपरीत दिशा में उत्पन्न विरोधी बल को गतिक घर्षण बल (Kinetic Frictional Force) कहते हैं। इसे यदि fk से निरूपित करें तब fk = µkR होता है।
यहाँ पर µk को गतिक घर्षण गुणांक (Coefficient of Kinetic Friction) कहते हैं। µk मात्रकहीन, विमाहीन राशि है।
दो सतहों के मध्य गतिक घर्षण गुणांक, गतिक घर्षण बल और | अभिलम्ब प्रतिक्रिया बल के अनुपात के बराबर होता है। सामान्यतः µk < µs होता है।
अर्थात् fk < fs, max
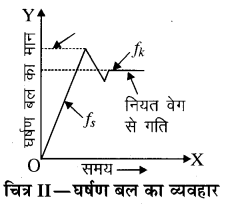
चित्र I में ब्लॉक पर लगाया गया बाह्य क्षैतिज बल F जैसे-जैसे बढ़ाया जाता है, घर्षण बल का मान भी बढ़ता जाता है, जब F = fs, max की सीमा के बाद भी बाह्य बल को बढ़ाते हैं, तब ब्लॉक गति करने लगता है और घर्षण बल का मान घटकर fk रह जाता है। इस अवस्था में नियत वेग से गति बनाये रखनी हो तब बाह्य बल को भी घटाकर fk के बराबर करना पड़ेगा। ऐसी अवस्था में (अर्थात् नियत वेग से गतिशील अवस्था में) बाह्य बल F, घर्षण बल fk के बराबर होता है। गतिशील अवस्था में fk लगभग नियत रहता है। इन तथ्यों को चित्र II में दिखाया गया है।
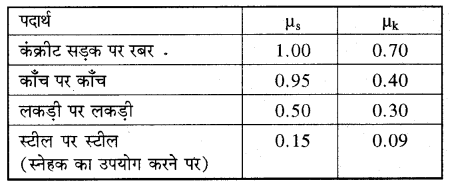
आगे दी गई सारणी में कुछ सतहों के लिए µs और µk
प्रश्न 9.
क्षैतिज तले में एक पिण्ड की वृत्ताकार गति को वर्णन कीजिए तथा आवर्तकाल के लिए सूत्र ज्ञात कीजिए।
उत्तर:
क्षैतिज एवं ऊर्ध्वाधर तल में वृत्तीय गति
(Circular Motion in Horizontal and Vertical Planes)
अभी तक हमने ऊपर जिस वृत्तीय गति का उल्लेख किया है, वह एक कण की वृत्तीय गति है। किसी वस्तु को हम एक रस्सी या धागे द्वारा बाँधकर क्षैतिज या ऊर्ध्वाधर तल में वृत्ताकार गति करवा सकते हैं। इसे हम निम्न प्रकार से समझ सकते हैं
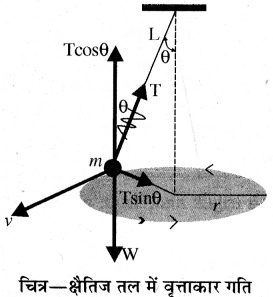
उपरोक्त चित्र में दर्शाये अनुसार एक द्रव्यमान m पर विचार करें। जो L लम्बाई के एक धागे के एक सिरे पर बँधा हुआ है। द्रव्यमान (m) एक नियत चाल v से एक क्षैतिज वृत्त में गति कर रहा है। जैसे-जैसे द्रव्यमान वृत्त में गति करता है, धागा एक θ कोण के शंकु की सतह को प्रसर्प (sweep) करता है, जहाँ θ धागे द्वारा ऊर्ध्व रेखा से बनाया गया कोण है। किसी क्षण पर द्रव्यमान m पर लगने वाले बलों को चित्र में दर्शाया गया है। यदि T धागे में तनाव है तो T के घटक T cos θ और T sin θ करने पर द्रव्यमान को आवश्यक अभिकेन्द्रीय बल T sin θ घटक से प्राप्त होता है। द्रव्यमान m में कोई ऊर्ध्वाधर त्वरण नहीं है। अतः घटक T cos θ द्रव्यमान के भार W से संतुलित होना चाहिए।
इस प्रकार
T sin θ = \(\frac{m v^{2}}{r}\) ……………(1)
T cos θ = W = mg …………. (2)
समीकरण (1) में समीकरण (2) का भाग देने पर

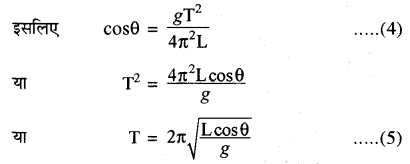
समीकरण (4) से θ कोण का आवर्तकाल T से सम्बन्ध ज्ञात होता है। इस समीकरण से θ का मान 90° नहीं हो सकता क्योंकि उसके लिए T को शून्य होना पड़ेगा या v = ∞
पुनः T का अधिकतम मान
Tmax = \(2 \pi \sqrt{\frac{L}{g}}\) होगा, जो कि अत्यल्प कोण (θ ≈ 0) के लिए सम्भव है ताकि cos θ ≈ cos θ = 1
समीकरण (5) एक सरल लोलक के लिए आवर्तकाल के व्यंजक के समान है, जिसका अध्ययन हम अध्याय-8 में करेंगे। इस समानता के कारण उपरोक्त युक्ति को शंकु-लोलक भी कहते हैं।
अब हम एक द्रव्यमान m की जो r लम्बाई के एक धागे के एक सिरे से बँधा है, की ऊर्ध्वाधर तल में वृत्तीय गति पर विचार करते हैं। चित्र में दिखाये अनुसार द्रव्यमान m पर दो बल कार्यरत हैं, एक इसका भार W = mg तथा दूसरी धागे में तनाव T है। भार W को चित्र में दर्शाये अनुसार दो घटकों में वियोजित करने पर हमें परिणामी स्पर्श रेखीय एवं अभिलम्बीय बल प्राप्त होते हैं ।
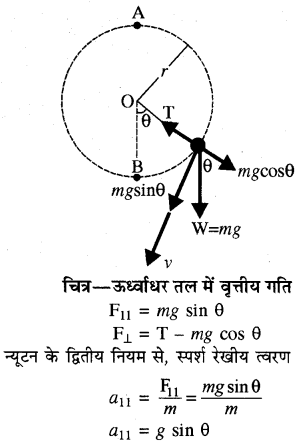
यह त्वरण का व्यंजन उसी प्रकार का है जैसा एक θ ढाल कोण वाले नत तल पर m द्रव्यमान के सर्पण (sliding) से प्राप्त होता है। अभिलम्बीय त्वरण ही कण को आवश्यक अभिकेन्द्रीय त्वरण प्रदान करता है, जिसका मान होगा

चित्र में दर्शाये अनुसार वृत्त के निम्नतम बिन्दु B पर θ = 0, sin θ = 0 तथा cos θ = 1 अतः इस बिन्दु पर F11 = 0, a11 = 0 तथा द्रव्यमान m का त्वरण शुद्ध रूप से अभिकेन्द्रीय (ऊपर की ओर) होगा तथा इस बिन्दु पर धागे में तनाव समीकरण (6) से θ = 0 रखने पर प्राप्त होता है।
TB = \(m\left(\frac{v^{2}}{r}+g\right)\) ………….. (7)
चित्र में दर्शाये अनुसार वृत्त के उच्चतम बिन्दु A पर θ = 180°, sin θ= 0 तथा cos θ =- 1. तथा त्वरण पुनः शुद्ध रूप से अभिकेन्द्रीय (नीचे की ओर) होगा तथा इसका मान
TA = \(m\left(\frac{v^{2}}{r}-g\right)\) ……………(8)
समीकरण (8) से हम उच्चतम बिन्दु A पर क्रान्तिक वेग का मान ज्ञात कर सकते हैं। जहाँ पर धागे में तनाव शून्य हो जाये या धागा ढीला हो जाये। माना कि यह वेग vc है। इसका मान समीकरण (8) में | TA = 0 रखने पर ज्ञात होता है। अतः
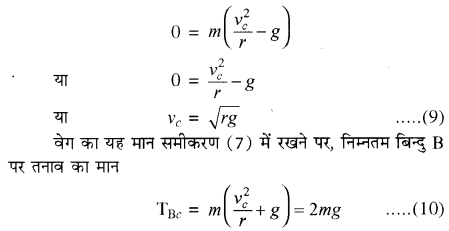
प्रश्न 10.
ऊर्ध्वाधर तल में एक पिण्ड की वृत्ताकार गति का वर्णन करिए। वृत्त के उच्चतम एवं निम्नतम बिन्दुओं पर एक डोरी में उत्पन्न तनाव के लिए सूत्रे ज्ञात कीजिए। क्रान्तिक वेग किसे कहते हैं? इसका सूत्र ज्ञात कीजिए।
उत्तर:
क्षैतिज एवं ऊर्ध्वाधर तल में वृत्तीय गति
(Circular Motion in Horizontal and Vertical Planes)
अभी तक हमने ऊपर जिस वृत्तीय गति का उल्लेख किया है, वह एक कण की वृत्तीय गति है। किसी वस्तु को हम एक रस्सी या धागे द्वारा बाँधकर क्षैतिज या ऊर्ध्वाधर तल में वृत्ताकार गति करवा सकते हैं। इसे हम निम्न प्रकार से समझ सकते हैं

उपरोक्त चित्र में दर्शाये अनुसार एक द्रव्यमान m पर विचार करें। जो L लम्बाई के एक धागे के एक सिरे पर बँधा हुआ है। द्रव्यमान (m) एक नियत चाल v से एक क्षैतिज वृत्त में गति कर रहा है। जैसे-जैसे द्रव्यमान वृत्त में गति करता है, धागा एक θ कोण के शंकु की सतह को प्रसर्प (sweep) करता है, जहाँ θ धागे द्वारा ऊर्ध्व रेखा से बनाया गया कोण है। किसी क्षण पर द्रव्यमान m पर लगने वाले बलों को चित्र में दर्शाया गया है। यदि T धागे में तनाव है तो T के घटक T cos θ और T sin θ करने पर द्रव्यमान को आवश्यक अभिकेन्द्रीय बल T sin θ घटक से प्राप्त होता है। द्रव्यमान m में कोई ऊर्ध्वाधर त्वरण नहीं है। अतः घटक T cos θ द्रव्यमान के भार W से संतुलित होना चाहिए।
इस प्रकार
T sin θ = \(\frac{m v^{2}}{r}\) ……………(1)
T cos θ = W = mg …………. (2)
समीकरण (1) में समीकरण (2) का भाग देने पर

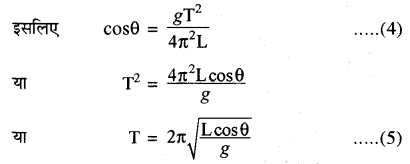
समीकरण (4) से θ कोण का आवर्तकाल T से सम्बन्ध ज्ञात होता है। इस समीकरण से θ का मान 90° नहीं हो सकता क्योंकि उसके लिए T को शून्य होना पड़ेगा या v = ∞
पुनः T का अधिकतम मान
Tmax = \(2 \pi \sqrt{\frac{L}{g}}\) होगा, जो कि अत्यल्प कोण (θ ≈ 0) के लिए सम्भव है ताकि cos θ ≈ cos θ = 1
समीकरण (5) एक सरल लोलक के लिए आवर्तकाल के व्यंजक के समान है, जिसका अध्ययन हम अध्याय-8 में करेंगे। इस समानता के कारण उपरोक्त युक्ति को शंकु-लोलक भी कहते हैं।
अब हम एक द्रव्यमान m की जो r लम्बाई के एक धागे के एक सिरे से बँधा है, की ऊर्ध्वाधर तल में वृत्तीय गति पर विचार करते हैं। चित्र में दिखाये अनुसार द्रव्यमान m पर दो बल कार्यरत हैं, एक इसका भार W = mg तथा दूसरी धागे में तनाव T है। भार W को चित्र में दर्शाये अनुसार दो घटकों में वियोजित करने पर हमें परिणामी स्पर्श रेखीय एवं अभिलम्बीय बल प्राप्त होते हैं ।

यह त्वरण का व्यंजन उसी प्रकार का है जैसा एक θ ढाल कोण वाले नत तल पर m द्रव्यमान के सर्पण (sliding) से प्राप्त होता है। अभिलम्बीय त्वरण ही कण को आवश्यक अभिकेन्द्रीय त्वरण प्रदान करता है, जिसका मान होगा

चित्र में दर्शाये अनुसार वृत्त के निम्नतम बिन्दु B पर θ = 0, sin θ = 0 तथा cos θ = 1 अतः इस बिन्दु पर F11 = 0, a11 = 0 तथा द्रव्यमान m का त्वरण शुद्ध रूप से अभिकेन्द्रीय (ऊपर की ओर) होगा तथा इस बिन्दु पर धागे में तनाव समीकरण (6) से θ = 0 रखने पर प्राप्त होता है।
TB = \(m\left(\frac{v^{2}}{r}+g\right)\) ………….. (7)
चित्र में दर्शाये अनुसार वृत्त के उच्चतम बिन्दु A पर θ = 180°, sin θ= 0 तथा cos θ =- 1. तथा त्वरण पुनः शुद्ध रूप से अभिकेन्द्रीय (नीचे की ओर) होगा तथा इसका मान
TA = \(m\left(\frac{v^{2}}{r}-g\right)\) ……………(8)
समीकरण (8) से हम उच्चतम बिन्दु A पर क्रान्तिक वेग का मान ज्ञात कर सकते हैं। जहाँ पर धागे में तनाव शून्य हो जाये या धागा ढीला हो जाये। माना कि यह वेग vc है। इसका मान समीकरण (8) में | TA = 0 रखने पर ज्ञात होता है। अतः
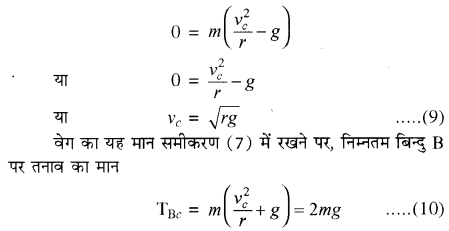
प्रश्न 11.
एक समतल वृत्ताकार पथ पर एक वाहन की गति का वर्णन करते हुए वाहन की अधिकतम गति के लिए आवश्यक सूत्र ज्ञात कीजिए।
उत्तर:
समतल वृत्ताकार (Motion of a vehicle on Circular path)
माना m द्रव्यमान का एक वाहन, r त्रिज्या की एक समतल वृत्ताकार सड़क पर नियत चाल v से गति कर रहा है। इस वाहन पर लगने वाले बल चित्र में दिखाये गये हैं। वाहन को भार mp नीचे की ओर है तथा सड़क के कारण वाहन पर लगने वाला प्रतिक्रिया बल R ऊर्ध्वाधर ऊपर की ओर है। वृत्ताकार मोड़ पर वाहन के पहिये, वृत्ताकार पथ के केन्द्र से दूर जाने का प्रयास करते हैं, जिसके कारण टायरों व सड़क के मध्य घर्षण बल f पहियों के अक्ष पर पथ के केन्द्र O की ओर लगता है। यदि घर्षण गुणांक µ है तो। घर्षण बल
f ≤ µR
ऊर्ध्व बलों के सन्तुलन से mg = R
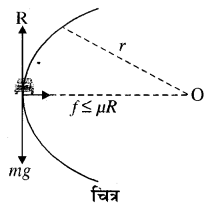
यह घर्षण बल f ही वृत्ताकार पथ में गति के लिए आवश्यक अभिकेन्द्रीय बल \(\frac{m v^{2}}{r}\) प्रदान करता है।
अर्थात् f = \(\frac{m v^{2}}{r}\) ……………. (1)
इस प्रकार समतल वृत्ताकार पथ पर वाहन की सुरक्षित गति के लिए वाहन पर कार्यरत अभिकेन्द्रीय बल का मान घर्षण बल के बराबर या इससे कम होना चाहिए।
इस प्रकार समतल वृत्ताकार पध पर नियत चाल से गति करने के लिए चाल की एक अधिकतम सीमा निम्न समीकरण द्वारा दी जाती है
vmax = \(\sqrt{\mu r g}\) ……………… (3)
यदि वाहन इससे अधिक चाल से गति करे तो वह वृत्ताकार पथ के केन्द्र O से दूर (सड़क के बाहर) की ओर फिसल जायेगा इसलिए वर्षा के दिनों में समतल वृत्ताकार पथ पर वाहन की चाल निर्धारित अधिकतम चाल से बहुत कम रखनी चाहिए।
प्रश्न 12.
वृत्ताकार मोड़ पर एक सड़क को बंकित क्यों किया जाता है? ऐसे मोड़ पर एक वाहन की अधिकतम गति के लिए आवश्यक सूत्र ज्ञात कीजिए। यदि सड़क में घर्षण को नगण्य मान लिया जाय तो बंकन कोण के लिए सूत्र ज्ञात कीजिए।
उत्तर:
वृत्ताकार घुमाव पर सड़क के बाहरी किनारे को कुछ उठाने को सड़क में करवट (banking) कहते हैं। इससे वृत्ताकार मोड़ पर वाहनों के अधिकतम सुरक्षित वेग में वृद्धि हो जाती है।
माना कि करवट ली हुई सड़क का करवट कोण θ है तथा वृत्ताकार पथ की त्रिज्या r है। mg भार का एक वाहन v नियत चाल से गतिशील है। किसी क्षण वाहने पर निम्न बल लगते हैं
(i) वाहन का भार mg ऊध्र्वाधर नीचे की ओर और
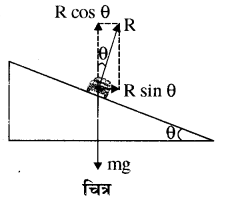
(ii) प्रतिक्रिया बल R सड़क के लम्बवत् ऊपर की ओर लगता है। अर्थात् प्रतिक्रिया बल R ऊध्र्वाधर दिशा से θ कोण पर लगता है। इस प्रतिक्रिया बल R के दो क्रमिक परस्पर लम्बवत् ऊध्र्वाधर घटक R cos 8 और क्षैतिज घटक R sin θ हैं। ऊर्ध्वाधर घटक (R cos θ) वाहन के भार mg को सन्तुलित करता है जबकि क्षैतिज घटक (R sin θ) वृत्ताकार पथ में गति के लिए आवश्यक अभिकेन्द्रीय बल उपलब्ध कराता है।
R cos θ = mg ……………(1)
R sin θ = \(\frac{m \mathrm{v}^{2}}{r}\) …………. (2)
समीकरणं (2) में समीकरण (1) का भाग देने पर
\(\frac{\mathrm{R} \sin \theta}{\mathrm{R} \cos \theta}=\frac{m \mathrm{v}^{2} / r}{m g}\)
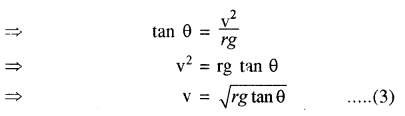
समीकरण (3) वाहन की आदर्श चाल के समीकरण को व्यक्त करता है। यह एक करवट कोण वाली सड़क के लिए r त्रिज्या के वृत्ताकार मोड़ पर घर्षण की अनुपस्थिति में वाहन की इष्टतम (optimini) चाल है। इस चाल पर वाहन के टायरों पर त्रिज्यीय दाब | नहीं होगा और टायरों में जीर्ण-शीर्ण न्यूनतम रहेगा।
कोणीय विस्थापन (Angular Displacement)
माना एक कण । त्रिज्या के वृत्ताकार पथ में गति कर रहा है, जिसका केन्द्र O है। जैसा सामने चित्र में दर्शाया गया है। कण समय पर स्थिति A पर है, जो रेखा OX से कोण 8 की स्थिति है। माना At समय में कण B पर पहुँच जाता है, जहाँ ∠BOX = θ + Δθ है । तब Δt समयान्तराल में कण का कोणीय विस्थापन निम्न है, कोणीय विस्थापन = Δθ = ∠BOA कोणीय विस्थापन का SI मात्रक रेडियन है। यह एक विमाहीन राशि है।
प्रश्न 13.
एक आनत तल पर एक पिण्ड की गति का वर्णन करिये।
उत्तर:
विराम कोण (Angle of Repose)
आनत तल का क्षैतिज दिशा के साथ वह अधिकतम झुकाव कोण, जिस पर वस्तु का आनत तल पर ठीक सन्तुलन की अवस्था में बनी रहती है, उसे विराम कोण कहते हैं।
नत कोण θ0 वाले आनत तल पर रखे M द्रव्यमान की वस्तु पर कार्यरत बल चित्रानुसार है।
सन्तुलन की स्थिति में
सीमान्त घर्षण (fs)max = µsR = Mg sin θ0 ……….. (1)
अभिलम्ब प्रतिक्रिया R = Mg cos θ0 ……………(2)
समीकरण (1) में समीकरण (2) का भाग देने पर

अर्थात् घर्षण कोण तथा विश्राम कोण समान होते हैं। इस प्रकार नत कोण θ ≤ θ0 पर वस्तु स्थिर तथा θ > θ0 , पर वस्तु फिसलने लगती है।
प्रश्न 14.
जड़त्वीय एवं अजड़त्वीय निर्देश तंत्रों में अन्तर स्पष्ट करिये। क्या पृथ्वी जड़त्वीय निर्देश तंत्र है? स्पष्ट करिये।
उत्तर:
जड़त्वीय निर्देश तन्त्र (Inertial frame of reference)- एक ऐसा निर्देश तन्त्र जिसमें न्यूटन का गति का प्रथम नियम (अर्थात् जड़त्व का नियम) मान्य रहे, जड़त्वीय निर्देश तन्त्र कहलाता है। ऐसे निर्देश तन्त्र में, एक कण पर बाह्य बल नहीं लग रहा हो, तो वह कण सदैव एक सरल रेखा में नियत वेग से गति करता है।
यदि हम पृथ्वी पर जड़े हुए एक निर्देश तन्त्र की कल्पना करें तब पृथ्वी की घूर्णन गति और परिक्रमण गति के कारण निर्देश तन्त्र में भी ये दोनों गतियाँ होंगी, इस कारण पूर्ण रूप से ऐसे निर्देश तन्त्र को जड़त्वीय निर्देश तन्त्र नहीं कह सकते दूरस्थ तारों के सापेक्ष एक स्थिर निर्देश तन्त्र को जड़त्वीय निर्देश तन्त्र माना जा सकता है। एक जड़त्वीय निर्देश तन्त्र के सापेक्ष स्थिर अन्य निर्देश तन्त्र भी जड़त्वीय होता है। एक जड़त्वीय निर्देश तन्त्र के सापेक्ष समान वेग से गतिशील अन्य देश तन्त्र भी जड़त्वीय निर्देश तन्त्र होता है। न्यूटन के गति के तीनों नियमों के कथन भी विशुद्ध रूप से एक जड़त्वीय निर्देश तन्त्र में ही मान्य हैं । यदि एक जड़त्वीय निर्देश तन्त्र में किसी कण पर लग रहा बल \(\overrightarrow{\mathrm{F}}\) और उत्पन्न त्वरण \(\vec{a}\) है (\(\overrightarrow{\mathrm{F}}=m \vec{a}\)) तब किसी दूसरे जड़त्वीय निर्देश तन्त्र, चाहे वह पहले के सापेक्ष स्थिर हो या नियत वेग से गतिशील हो, में कण पर लग रहा बल \(\overrightarrow{\mathrm{F}}\) ही प्रतीत हो। और त्वरण भी है \(\vec{a}\) प्राप्त होगा।
अजड़त्वीय निर्देश तन्त्र (Non-inertial frame of reference)— वे निर्देश तन्त्र जिनमें न्यूटन का गति का प्रथम नियम अर्थात् जड़त्व का नियम मान्य प्रतीत नहीं हो, अजड़त्वीय निर्देश तन्त्र कहलाते हैं। एक अजड़त्वीय निर्देश तन्त्र में एक स्वतन्त्र कण का पथ आवश्यक नहीं कि सरल रेखा में ही आये। एक जड़त्वीय निर्देश तन्त्र के सापेक्ष त्वरित निर्देश तन्त्र अजड़त्वीय निर्देश तन्त्र होता है। एक निर्देश तन्त्र जो किसी के सापेक्ष घूर्णन कर रहा है, वह भी एक अजड़त्वीय निर्देश तन्त्र होता है।
क्या पृथ्वी जड़त्वीय निर्देश तंत्र है?– यदि पृथ्वी से संबद्ध जड़त्वीय निर्देश तंत्र पर विचार करें तो यह जड़त्वीय निर्देश तंत्र नहीं है। क्योंकि पृथ्वी न केवल अपनी स्वयं की अक्ष पर अपितु सूर्य के चारों ओर भी घूर्णन करती है। पृथ्वी की स्वयं की घूर्णन गति के कारण इसकी सतह पर रखा कोई स्थिर कण इसके केन्द्र की ओर अभिकेन्द्री बल का अनुभव करता है। उदाहरणतः भूमध्य रेखा पर इस अभिकेन्द्री त्वरण का मान
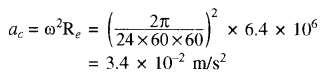
सामान्य यांत्रिकी की समस्याओं में इस त्वरण को यदि न्यून मान कर छोड़ दें तो पृथ्वी को जड़त्वीय निर्देश तंत्र माना जा सकता है परन्तु कतिपय समस्याओं में, इस त्वरण के प्रभाव दृष्टिगोचर होते हैं।
RBSE Class 11 Physics Chapter 4 आंकिक प्रश्न
प्रश्न 1.
कोई बॉक्स रेलगाड़ी के फर्श पर स्थिर रखा है। यदि बॉक्स तथा रेलगाड़ी के फर्श के बीच स्थैतिक घर्षण गुणांक 0.13 है। तो रेलगाड़ी का वह अधिकतम त्वरण ज्ञात कीजिये जो बॉक्स को रेलगाड़ी के फर्श पर स्थिर रखने के लिये आवश्यक है। (g = 9.8 ms-2)
हल:
दिया गया है
स्थैतिक घर्षण गुणांक (µs) = 0.15
रेलगाड़ी का अधिकतम त्वरण (amax) = ?
चूँकि बॉक्स में त्वरण स्थैतिक घर्षण के कारण ही है इसलिए
ma = (fs)max ≤ µsR = µs mg
∵ R = mg
अर्थात्
a ≤ µs g
amax = µs g
= 0.13 × 9.8
= 1.274 m/s2
a = 1.27 m/s2
प्रश्न 2.
18 km/h की चाल से समतल सड़क पर गतिमान कोई साइकिल सवार बिना चाल को कम किये 3m त्रिज्या का तीव्र वर्तुल मोड़ लेता है, टायरों तथा सड़क के बीच स्थैतिक घर्षण गुणांक 0.1 है। क्या साइकिल सवार मोड़ लेते समय फिसल कर गिर जायेगा?
हल:
दिया गया है- V = 18 km/h

vmax = 1.71 m/s से अधिक चलाने पर साइकिल सवार फिसलकर गिर जायेगा।
प्रश्न 3.
किसी विस्फोट में एक बम के तीन टुकड़े हो जाते हैं जिसके दो टुकड़े एक-दूसरे के लम्बवत् गति करते हैं। यदि प्रथम टुकड़े का द्रव्यमान 2 kg व वेग 12 ms-1, दूसरे का द्रव्यमान 1 kg व वेग 8 ms2 तथा तीसरे टुकड़े का वेग 20 ms2 हो तो उसके द्रव्यमान की गणना कीजिये।
हल:
दिया गया है- m1= 2 kg, m2 = 1 kg, m3 = ?
v1 = 12 m/s, v2 = 8 m/s, v2 = 20 m/s
संवेग संरक्षण नियम से

प्रश्न 4.
किसी हल्की घर्षणरहित घिरनी पर चढ़ी डोरी के दो सिरों पर 8 kg व 12 kg द्रव्यमान के दो पिण्डों को बाँधा गया है। पिण्डों को मुक्त छोड़ने पर उनके त्वरण तथा डोरी में तनाव ज्ञात कीजिये।
हल:
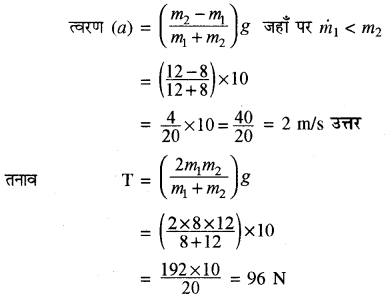
प्रश्न 5.
कोई बल्लेबाज किसी गेंद को 45° के कोण पर विक्षेपित कर देता है। ऐसा करने पर वह गेंद की आरम्भिक चाल 54 kmh-1 में कोई परिवर्तन नहीं करता है तो गेंद के आवेग की गणना कीजिये यदि गेंद का द्रव्यमान 0.15 kg हो।
हल:
माना m द्रव्यमान की गेंद u वेग से गतिमान है। इसकी दिशा AO के अन्तर्गत है। यह बल्ले ML से टकराकर OB के अंनुदिश प्रक्षिपित होती है तथा ∠AOB = 45° माना ON बल्ले पर अभिलम्ब है।
NO के अनुदिश चाल को घटक u cos θ है।
NO = u cos θ
ON के अनुदिश अन्तिम वेग का घटक – u cos θ है।
NO = – u cos θ
यहाँ पर ऋण चिन्ह यह दर्शाता है कि अन्तिम वेग आरम्भिक वेग की विपरीत दिशा में है। अर्थात् ऊर्ध्वाधर के अनुदिश वेग केवल पलट जाता है।
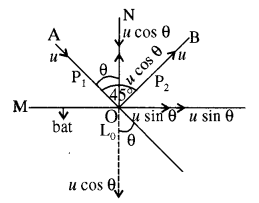
अतः गेंद का NO के अनुदिश आरम्भिक संवेग
NO = mu cos θ
तथा ON के अनुदिश गेंद का अन्तिम संवेग
ON = – mu cos θ
इस प्रकार गेंद को प्रदत्त आवेग = गेंद के रैखिक संवेग में परिवर्तन
= – mu cos θ – mu cos θ
= – 2 mu cos θ …………..(1)
दिया गया है
m = 0.15 kg,
u = 54 km/h
u = 54 × \(\frac{5}{18}\)
= 3 × 5
= 15 m/s
θ = 22.5°
समीकरण (1) में मान रखने पर
आवेग = – 2 × 0.15 × 15 × cos 22.5°
= – 4.5 × 0.9239
= – 4.16 kg m/s
∴ आवेग का परिमाण 4.2 kg m/s
प्रश्न 6.
15 ms-1 की आरम्भिक चाल से गतिशील 20 kg द्रव्यमान के एक पिण्ड पर 50 N का स्थाई मंदन बल आरोपित है तो पिण्ड को रुकने में लगे समय की गणना कीजिये।
हल:
दिया गया हैआरम्भिक चाल (u) = 15 m/s
m = 20 kg
F = – 50 N (मंदन बल)
v = 0 m/s, t = ?
∵ F = ma
⇒ a = \(\frac{\mathrm{F}}{m}=\frac{-50}{20}\) = 20 m/s
= – 2.5 m/s2
∵ v = u + at
0 = 15 + (- 2.5) t
⇒ 1 = \(\frac{15}{2.5}\) = 6 second
प्रश्न 7.
100 kg द्रव्यमान की किसी तोप से 0.020 kg का गोला दागा जाता है। यदि गोले की नालमुखी चाल 80 ms-1 है तो तोप की प्रतिक्षेप चाल क्या होगी?
हल:
M = 100 kg
m = 0.020 kg
v = 80 m/s
V = ?
संवेग संरक्षण नियम से
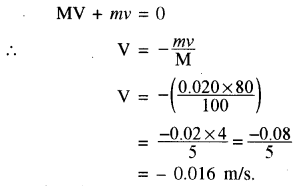
अतः तोप की प्रतिक्षेप चाल = 0.016 m/s
प्रश्न 8.
यदि 0.1 kg द्रव्यमान के एक कण की गति y = 0.3t + \(\frac{9.8}{2} t^{2}\) से वर्णित है तो उसे कण पर लगने वाले बल की गणना कीजिये।
हल:

प्रश्न 9.
किसी डोरी के एक सिरे से बँधा 0.25 kg संहति का कोई पत्थर क्षैतिज तल में 1.5 m त्रिज्या के वृत्ताकार पथ पर 40 rev/min की चाल से चक्कर लगाता है। डोरी में तनाव कितना है? यदि डोरी 200 N के अधिकतम तनाव को सहन कर सकती है, तो वह अधिकतम चाल ज्ञात कीजिए जिससे पत्थर को घुमाया जा सकता है।
हल:
दिया गया है
पत्थर का द्रव्यमान m = 0.25 kg
वृत्त की त्रिज्या r = 1.5 m
तनाव Tmax = डोरी में अधिकतम तनाव = 200 N
Vmax = पत्थर की अधिकतम चाल = ?
40 चक्कर/मिनट लगाता है इसलिए
आवृत्ति f = \(\frac{40}{60}=\frac{2}{3}\) चक्कर/सेकण्ड
डोरी में तनाव T = ?
डोरी में तनाव (T) ही अभिकेन्द्रीय बल देता है।

अर्थात्
Vmax ≅ 35.0 m/s है। अतः
T = 6.6 N, Vmax = 35.0 m/s
प्रश्न 10.
5 kg द्रव्यमान के किसी पिण्ड पर 8N व 6N के दो लम्बवत् बल आरोपित हैं। पिण्ड के त्वरण का परिमाणं व दिशा ज्ञात कीजिये।
हल:
दिया गया है
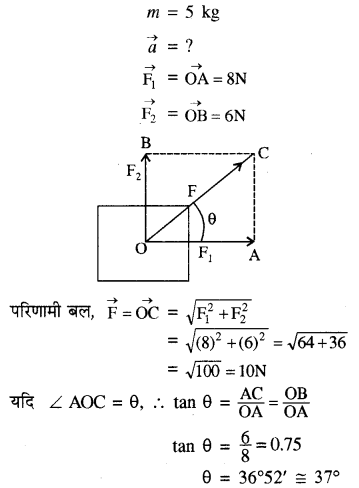
यह परिणामी बल की दिशा है अतः पिण्ड के त्वरण की दिशा, बल की दिशा ही होगी।
a = \(\frac{\mathrm{F}}{\mathrm{m}}=\frac{10}{5}\) = 2 m/s2
अतः त्वरण का परिमाण 2 m/s2 बल की दिशा में कार्य करता है।