RBSE Solutions for Class 12 Maths Chapter 1 Composite Functions Ex 1.1

by

Rajasthan Board RBSE Class 12 Maths Chapter 1 Composite Functions Ex 1.1

Question 1.
If f : R → R and g : R → R be two functions defined as below, then find (fog) (x) and (gof)(x):
(i) f(x) = 2x + 3, g(x) = x2 + 5
(ii) f(x)= x2 +8, g(x) = 3x3 +1
(iii) f(x) = x, g(x) = |x|
(iv) f(x) = x2 + 2x + 3, g(x) = 3x – 4
Solution:
(i) Given,
f(x) = 2x + 3 and g(x) = x2 + 5
(fog)(x) = f(g(x))
= f(x2 + 5)
= 2(x2 + 5) + 3
= 2x2 + 10 + 3
= 2x2 + 13

(gof)(x) = g(x))
= g(2x + 3)
= (2x + 3)2 + 5
= 4x2 + 9 + 12x + 5
= 4x2 + 12x + 14

(ii) Given, f(x)= x2 + 8 and g(x) = 3x3 + 1
(fog)(x) = f(g(x))
= f(3x3 + 1)
= (3x3 + 1)2 +8
= 9x6 + 6x3 + 1 +8
= 9x6 + 6x3 +9

(gof)(x) = g(f(x))
= g(x2 + 8)
= 3(x2 + 8)3 + 1

(iii) Given, f(x)=x and g(x) = |x|
(fog)(x) = f(g(x))
= f(|x|) = |x|
(gof)(x)=g(f(x))
= g(x) = |x|

(iv) Given, f(x)= x2 + 2x + 3 and g(x) = 3x – 4
(fog)(x) = f(g(x))
= f(3x – 4)
= (3x – 4)2 + 2(3x – 4) + 3
= 9x2 – 24x + 16 + 6x – 8 + 3
= 9x2 – 18x + 11

(gof)(x) = g(f(x)) = g(x2 + 2x + 3)
= 3(x2 + 2x + 3) – 4 = 3x2 + 6x + 9 – 4
= 3x2 + 6x + 5.

Question 2.
If A = {a,b,c}, B = {u, v, w}.
If f: A → B and g : B → A, defined as
f = {(a, v), (b, u), (c, w)}
g = {(u, b), (v, a), (w, c)}
then find (fog) and (gof).
Solution:
Given, f= {(a, v), (b, u), (c, w)}
g= {(u, b), (v, a), (w, c)}
f(a)= v and g(u) = b
f(b)= u and g(v) = a
f(c)= w and g(w) = C

So, from fog(x) = f(g(x)]
fog(u) = f(g(u)] = f(b) = u
fog(v) = f(g(v)] = f(a) = v
fog(w)= f[g(w)] = f(c) = w

So, fog = {(u, u), (v, v), (w, w)}
gof(a) = g[f(a)] = g(v) = a
gof(b) = g[fb)] = g(u) = b
gof(c) = g[(c)] = g(w) = C
gof = {(a, a), (b, b), (c, c)}

Question 3.
If f: R+ → R+ and g: R+ → R+, defined as f(x) = x2 and g(x)= √x, then find gof and fog. Are they identity functions ?
Solution:
Given,
f : R+ → R+, 4(x) = x2
g : R+ → R+, g(x) = √x
(gof)(x) = g[f(x)] = g(x2) = √x2 = x
(fog)(x) = f(g(x)] = f(√x) = (√x)2 = x
So, (fog)(x) = (gof)(x) = x, ∀ x ∈ R+
Hence, (fog) and (gof) are identity function.

Question 4.
If f : R → Rand g : R → R be such two functions that defined as f(x) = 3x +4 and g(x) = \(\frac { 1 }{ 3 }\) (x – 4), then find (fog)(x) and (gof)(x), also find (gog)(1).
Solution:
Given, f : R → R, f(x) = 3x + 4
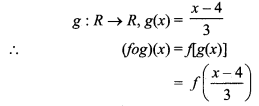
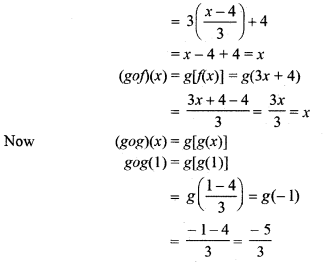
RBSE Solutions for Class 12 Maths Chapter 1 Composite Functions Ex 1.1
RBSE Solutions for Class 12 Maths Chapter 1 Composite Functions Ex 1.1

Question 5.
If f, g, h be three functions from R to R, defined as f(x) = x2, g(x) = cos x and h(x) = 2x + 3, then find {ho(gof)} (√2π).
Solution:
Given function,
f(x) = x2, g(x) = cos x, h(x) = 2x + 3
∴ {ho(gof)}(x) = hog{f(x)}
= h[g{f(x)}]
= h[g(x2)] = h(cos x2)
= 2 cos x2 + 3

{ho(gof)}√2π = 2 cos (√2π)2 + 3
= 2 cos 2π + 3
= 2 x 1 + 3 = 5

Question 6.
If functions f and g be defined as below, then find (gof)(x) :
f : R → R, f(x) = 2x + x-2
g : R → R, g(x) = x4 + 2x + 4
Solution:
Given, f: R → R
f(x) = 2x + x-2
g: R → M R, g(x)= x4 + 2x + 4.
∴ (gof)(x) = g(f(x)} = g{2x + x-2} = (2x + x-2)4 + 2(2x + x-2) + 4

Question 7.
If A = {1, 2, 3, 4}, f : R → R, f(x) = x2 + 3x + 1 g : R → R, 8(x) = 2x – 3, then find
(i) (fog)(x)
(ii) (gof)(x)
(iii) (fof)(x)
(iv) (gog)(x)
Solution:
Given,
f : R→ R, f(x) = x2 + 3x + 1
g : R → R, g(x) = 2x – 3

(i) (fog)(x) = f{g(x)}
= f{2x – 3}
= (2x – 3)2 + 3(2x – 3) + 1
= 4x2 – 12x + 9 + 6x – 9 + 1
= 4x2 – 6x + 1

(ii) (gof)(x) = g{f(x)}
= g(x2 + 3x + 1)
= 2(x2 + 3x + 1) – 3
= 2x2 + 6x + 2 – 3
= 2x2 + 6x – 1

(iii) (fof)(x) = f{f(x)}
= f(x2 + 3x + 1)
= (x2 + 3x + 1)2 + 3(x2 + 3x + 1)+1
= x4 + 9x2 + 1 + 6x3 + 6x + 2x2 + 3x2 + 9x + 3 + 1
= x4 +6x3 + 14x2 + 15x + 5

(iv) (gog)(x) = g{g(x)}
= g(2x – 3)
= 2(2x – 3) – 3
= 4x – 6 – 3
= 4x – 9

RBSE Solutions for Class 12 Maths