Rajasthan Board RBSE Class 12 Maths Chapter 1 Composite Functions Ex 1.2
Question 1.
If A = {1, 2, 3,4}, B = {a,b,c,d}, then define four bijection from A to B and also find their inverse functions.
Solution:
Given
A = {1, 2, 3, 4), B = {a, b, c, d}
(a) f1 = {(1, a),(2, b), (3, c), (4, d)}
f1-1 = {(a, 1), (1, 2), (c, 3), (d, 4)}
(b) f2 = {(1, a), (2, c), (3, b), (4, d)}
f2-1 = {(a, 1), (C, 2), (6, 3), (d, 4)}
(c) f3 = {(1, b), (2, a), (3, d), (4, b)}
f3-1 = {(b, 1), (a, 2), (d, 3), (6,4)}
(d) f4 = {(1, c), (2, d), (3, a),(4, b)}
f4-1 = {(c, 1), (d, 2), (a, 3), (b, 4)}
Question 2.
If f : R → R, such that f(x) = x3 – 3, then prove that f-1 exists and find its formula. Thus, find f-1(24) and f-1(5).
Solution:
Given, f : R → R, f(x) = x3 – 3
One-one/many-one:
Let a, b ∈ R
∴ f(a) = f(b)
⇒ a3 – 3 = b3 – 3
⇒ a3 = b3
⇒ a = b
Hence, . f(a) = f(b) ⇒ a = b
∴ f is a one-one function.
Onto/into:
Let y ∈ R (Co-domain)
f(x) = y
⇒ x3 – 3 = y
⇒ x= (y + 3)1/3 ∈ R, ∀ y ∈ R
Here, for each value of y, x exists in domain R.
Thus, Range of F= co-domain of f.
So, ‘f’ is onto function.
It is clear that ‘f is one-one onto function.
Hence, f-1: R → R exists.
f-1(y) = x ⇒ f(x) = y
But f(x)= x3 – 3
∴ x3 = 3 = y
⇒ x3 = y + 3
⇒ x = (y + 3)1/3
⇒ f-1(y) = (x + 3)1/3
⇒ f-1(x) = (x + 3)1/3, ∀ X ∈ R
For x = 24
∴ f-1(24)= (24 + 3)1/3
= (27)1/3
= 33 x 1/3 = 3
For x = 5
f-1(5) = (5 + 3)1/3
= (8)1/3
= 23 x 1/3 = 2
Question 3.
If f : R → R, defined as
(i) f(x) = 2x – 3
(ii) f (x) = x3 + 5
Then, prove that f is bijection in both conditions, Also find f-1.
Solution:
(i) Given function,
f : R → R, f(x) = 2x – 3
One-one/many-one:
Let a, b ∈ R
f(a) = f(b)
⇒ 2a – 3 = 2b – 3
⇒ 2a = 2b
⇒ a = b
So, f(a) = f(b) ⇒ a = b, ∀ a, b ∈ R
∴ f is one-one function.
onto/into:
Let y ∈ R (co-domain)
f(x)= y
⇒ 2x – 3 = y
⇒ x = \(\frac { y+3 }{ 2 }\) ∈ R , ∀ y ∈ R
So, pre-image for each value of y exists in domain R. Thus, function ‘f’ is onto function.
It is clear that ‘f’ is one-one into function.
Hence f-1 : R → R exists.
Let x ∈ R (domain of f)
and y ∈ R (co-domain of f)
Let f(x) = y, then f-1(y) = x
⇒ f(x) = y
⇒ 2x – 3 = y
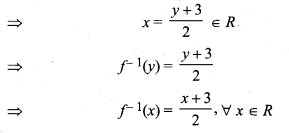
(ii) According to question,
f : R → R, f(x) = x3 + 5
One-one/onto : Let a, b ∈ R
f(a) = f(b)
⇒ a3 + 5 = b3 + 5
⇒ a3 = b3
a = b
So, f(a) = f(b)
⇒ a = b, ∀ a, b ∈ R
∴ f is one-one function
Onto/into:
Let y ∈ R (co-domain)
f(x) = y
⇒ x3 + 5 = y
⇒ x3 = y – 5
⇒ x = (y – 5)1/3 ∈ R, ∀ x ∈ R
So, pre-image for each value of y exists in domain R.
Thus, range of f = co-domain of f.
So, function ‘f’ is onto function.
Hence, we can say that f is one-one onto function.
So, f-1: R → R defined as
f-1(y)= x ⇔ f(x) = y ………(i)
⇒ f(x) = y
⇒ x3 + 5 = y
x3 = y – 5
⇒ x = ( y – 5)1/3
⇒ f-1(y)= (y – 5)1/3 [from (1)]
⇒ f-1(x) = (x – 5)1/3
Question 4.
If A = {1, 2, 3, 4), B = {3, 5, 7, 9), C = {7, 23, 47, 79} and f: A → B, g : B → C such that f(x) = 2x + 1 and g(x) = x2 – 2, then find (gof)-1 and f-1og-1 in ordered form.
Solution:
A = {1, 2, 3, 4), B = {3, 5, 7,9} and
C = {7, 23, 47, 79}
f : A → B, f (x) = 2x + 1
g : B → C, g(x) = x2 – 2
Now, gof (x)=g{f(x)} = g(2x + 1)
= (2x + 1)2 – 2 = 4x2 + 4x – 1
∴ gof (x) = 4x2 + 4x – 1
On putting x = 1, 2, 3, 4
gof = {(1,7), (2, 23), (3,47),(4, 79)}
∵ gof is bijection function.
∴ Its inverse is possible
⇒ (gof)-1 = {(7, 1), (23, 2), (47,3), (79,4)}
⇒ f-1og-1 = {(7,1), (23, 2) (47, 3), (79,4)}
[∵ (gof)-1 = f-1og-1 by theorem.
Question 5.
If f : R → R, such that f(x) = ax + b, a ≠ 0, then prove that f is a bijection function. Also, find f-1.
Solution:
Given function f : R→ R and ax + b, a ≠ 0
f-1 exists if f : R → R be a bijection function, before this we have to prove f be a bijection function.
One-one/many-one:
Let p, q ∈ R
f(p) = f(q)
⇒ ap + b = aq + b
⇒ ap = aq
⇒ p = q
So, f(p) = f(q), ∀ p, q ∈ R
∴ f is a bijection function.
Onto/into:
Let f(x) = y, y ∈ R
ax + b = y
⇒ x = \(\frac { y-b }{ a }\) ∈ R
So, pre-image of every value of y exist in domain R,
∴ ‘f’ is onto function.
Thus, range of f = co-domain of f.
So, f is a bijection function
So, f-1 exists.
Let, y ∈ R and f-1(y)= x,
then f(x) = y
⇒ ax +b = y
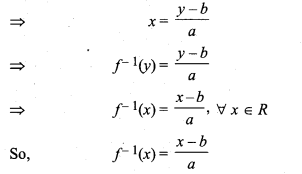
Question 6.
If f : R → R,f(x) = cos (x + 2), is f-1 exists.
Solution:
Given function
f : R → R, f(x) = cos (x + 2).
Putting x = 2π
f(2π) = cos (2π+ 2)
= cos (2)
Putting x = 0
f(0) = cos (0 + 2) = cos 2
Here, only one image is obtained for 0 and 2π.
So, ‘f’ is not one-one.
Thus, ‘f’ is not one-one onto.
Hence, f-1 : R → R does not exist.
Question 7.
Find f-1 (if exists), where f: A → B, such that
(i) A = {0,-1,- 3, 2}, B = {-9, – 3,0, 6}, f(x) = 3x
(ii) A = {1, 3, 5, 7,9}, B = {0, 1, 9, 25, 49, 81), f(x) = x2
(iii) A = B = R, f(x) = x3
Solution:
(i) Give function
f : A → B, f(x) = 3x where,
A = {0,-1,-3, 2}
B = {-9, – 3,0, 6}
Now, f(0)= 3 x 0 = 0
f(-1) = 3 x – 1 = -3
f(-3) = 3 x (- 3) = -9
f(2)= 3 x 2 = 6
So, f= {(0,0), (- 1, -3), (- 3,-9), (2, 6)}
Since, different element of A have different image in B under f.
So ‘f is one-one function.
Here, range of f = {-9, -3,0, 6} = B (co-domain).
So, f is onto function.
It is clear that ‘f’ is one-one onto function.
So, f-1 : B → A exist.
f-1 = {(0,0), (-3,- 1), (-9, – 3), (6, 2)}
(ii) Given function
f : A → B, f(x) = x2
where, A = {1, 3, 5, 7, 9}
B = {0, 1, 9, 25, 49, 81}
Now, f(1) = 12 = 1
f(3) = 32 = 9
f(5)= 52 = 25
f (7) = 72 = 49
f(9) = 92 = 81
So, f= {(1, 1), (3,9), (5, 25), (7,49), (9,81)}
Since, different element of A have different image in B under f.
So ‘f’ one-one function.
Here, range of R = {1,9, 25, 49, 81} ≠ B (co-domain)
∴ ‘f’ is not onto function.
Hence, f-1 does not exist.
(iii) Given, A = B = R, f(x) = x3
f(x)= x3
Let a, b ∈ R
and f(a) = f(b)
⇒ a3 = b3
a = b, ∀ a, b ∈ R
Let f(x)= y and y ∈ B or y ∈ R
∴ x3 = y
⇒ x = y1/3
Since, different element of A have different image of B under f.
So ‘f’ is one-one function.
and range of f= co-domain of f.
So, ‘f’ is onto function.
Hence, it is clear that f is one-one function f-1 exists.
If y is image of x under ‘f’, then
f-1 : B → A is defined
as f-1(y) = x ⇒ f(x) = y
⇒ x3 = y
⇒ x = y1/3
⇒ f-1(y) = y1/3
⇒ f-1(x) = x1/3
So, f-1: B → A, f-1(x) = x1/3, ∀ x ∈ B.