RBSE Solutions for Class 12 Maths Chapter 1 Composite Functions Ex 1.3

Rajasthan Board RBSE Class 12 Maths Chapter 1 Composite Functions Ex 1.3

Question 1.
Determine whether each of the following operation define a binary operation on the given set or not. Also, Justify your answer.
(i) a*b = a, on N
(ii) a*b = a + b – 3, on N
(iii) a*b = a + 3b, on N
(iv) a*b = a/b, on Q
(v) a*b = a – b, on R
Solution:
(i) a*b = a, on N
Here, * is a binary operation because
a, b ∈ N
= a*b = a ∈ N
Here, a*b ∈ N
Hence, * is a binary operation.

(ii) a*b = a + b – 3 ∈ N
Here, a*b is not a binary operation because,
1 ∈ N, 2 ∈ N
then 1 + 2 – 3 = 0 ∈ N

(iii) a*b= a + 3b ∈ N
Here, * is a binary operation because
1 ∈ N, 2 ∈ N
then 1 + 3 × 2 = 1 + 6 = 7 ∈N

(iv) a*b = \(\frac { a }{ b }\) ∈ Q
Here, a*b is not a binary operation because,
Let a = 22 ∈ Q and b= 7 ∈ Q
But

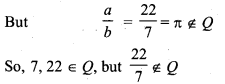
(v) a*b= a – b ∈ R
Here, * is a binary operation because,
a ∈ R, b ∈ R
⇒ a – b ∈ R, ∀ a, b ∈ R

Question 2.
Determine which of the following binary operation is commutative and which is associative :
(i) * on N defined as a*b = 2^ab
(ii) * on N defined as a*b = a + b + a^ab
(iii) * on Z defined as a*b = a – b
(iv) * on Q defined as a*b = ab + 1
(v) * on R defined as a*b = a + b – 7
Solution:
(i) Given a*b = 2^ab
Commutativity: Let a, b ∈ N
a*b = 2^ab
= 2^b.a
= b*a
So, a*b = b*a
∴ * is a commutative operation.

Associativity: Let a, b, c ∈ N
(a*b)*c = 2(ab)*2^c = 2^{ab + c}
= 2^c*2^(ab) = 2^{c +ab}
a*(b*c) = 2a*2^(bc) = 2^{a + bc}
2^ab+c ≠ 2^a+bc
It is clear that (a*b)*c ≠ a*(b*c)
So, (a*b)*c is not an associative operation.
Hence, a*b = 2^ab is commutative but not associative.

(ii) Given a*b= a + b + a²b
Commutativity: Let a, b ∈ N
a*b = a + b + a²b
b*a = b + a + b²a
a*b ≠ b*a .
So, * is not a commutative operation.

Associativity: Let a, b, c ∈ N
(a*b)*c = (a + b + a²b)*c
a*(b*c) = a*(b + c + b²c)
t is clear that (a*b)*c ≠ a*(b*c)
So * is not an associative operation.
Hence, a*b = a + b + a²b is neither commutative nor associative.

(iii) Given, a*b = a – b
Commutativity:
a*b = a – b, (a, b ∈ Z)
b*a = b – a, (a, b ∈ Z)
a*b* ≠ b*a
So * is not a commutative operation.

Associativity :
(a*b)*c = (a – b)*c
= a – b-c
a*(b*c) = a*(b-c)
= a – b + c
∵ (a*b)*c ≠ a*(b*c)
So, it is not associative operation.
It is clear that
a*b = a – b is neither commutative nor associative.

(iv) Given, a*b = ab + 1
Commutativity: Let a, b ∈ Q
a*b = ab + 1 and : b*a= ba + 1
⇒ a*b= b*a
∴ It is commutative.
∴ Addition and multiplication of rational number is commutative.

Associativity: Let a, b, c ∈ Q
(a*b)*c = (ab + 1)*c
= ab + 1 + c
(b*c)*a = (bc + 1) +a
= (a*b)*c ≠ (b*c)*a
So, * is not associative.
It is clear from above that a*b = ab + 1 is commutative but not associative.

(v) Given, a*b = a + b – 7
Commutativity: In R,
a*b = a + b – 7
= b + a – 7
= b*a’

Associativity :
(a*b)*c = (a + b – 7)*c
= (a + b – 7) + c – 7
= a + b + c – 14
a*(b*c) = a*(b + c – 7)
= a + (b + c – 7) – 7
= a + b + c – 14
So, (a*b)*c = a*(b*c)
Hence, it is clear that a*b = a + b – 7 are commutative and associative.

Question 3.
If * be an operation on Z, defined as a*b = a + b + 1, ∀ a, b ∈ Z then prove that * is commutative and associative, find its identity element. Also, find inverse element of any integer in Z.
Solution:
Given a*b = a + b + 1, ∀ a, b ∈ z

Commutativity :
a*b = a + b + 1
a*b = b + a + 1
= b*a
∴ a*b = b*a
∴ * is commutative operation.

Associativity :
(a*b) * c = (a + b + 1)*c
= a + b + 1 + c +1
a + b + c + 2
Again a*(b*c) = a*(b + c + 1)
= a + b + c + 1 + 1
= a + b + c + 2
a*(b*c)= (a*b)*c
∴ * is associative operation
Identity : If e is identity element, then
a*e = a
⇒ a + e + 1 = a
⇒ e = -1
So, – 1 ∈ Z is identity element.
Inverse : Let inverse of a is x, then by definition
a*x = -1 [∵ – 1 is identity]
⇒ a + x + 1 = -1
⇒ x = -(a + 2) ∈ Z
Inverse element a^-1 = -(a + 2).

Question 4.
If * be a binary operation defined on R – {1}. as a*b = a + b – ab, ∀ a, b ∈ R – {1}
prove that * is commutative and associative. Find identity element and also find inverse of a.
Solution:
If a, b ∈ R – {1} by definition
a*b = a + b – ab
= b + a – ba
= b*a
∴ * is a binary operation.
Again, (a*b)*c = (a + b – ab)*c
= (a + b – ab) + c – (a + b – ab)c
= a + b – ab + c – ac – bc + abc
= a + b +c – ab – bc – ac + abc …(i)
and a*(b*c) = a*(b + c – bc)
= a + (b + c – bc) – a (b + c – bc)
= a + b + c – bc – ab – ac + abc
= a + b + c – ab – bc – ac + abc … (ii)
From eqs. (i) and (ii),
(a*b)*c= a*(b*c)
∴ * is associative operation.
Let e is identity of *, then for a ∈ R,
a*e = a (from definition of identity)
⇒ a + e – ae = a
⇒ e(1 – a)= 0
⇒ e = 0 ∈ R – {1}
∵ 1 – a ≠ 0
∴ 0 is identity of *.
Let b is inverse of a.
a*b = e
a + b – ab = 0.e
b – ab = -a
b(1 – a) = -a

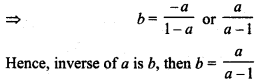
Question 5.
Four functions are defined on set R_o, Such that,
f₁(x) = x, f₂(x) = -x, f₃(x) = 1/x, f₄(x) = – 1/x Construct the composition table for the composition of functions f₁, f₂, f₃, f₄. Also, find identity element and inverse of every element.
Solution:
Given,
f₁(x) = x, f₂(x) = – x,



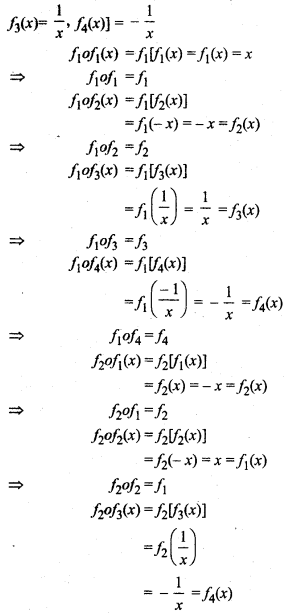
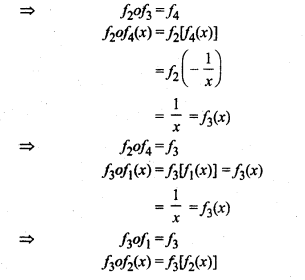
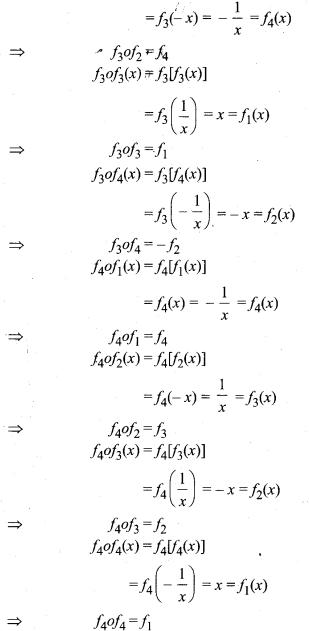
∴ Table for above operations

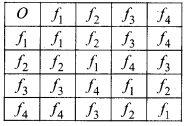
Hence, it is clear that f₁ is identity function of f₁, f₂, f₃, f₄.
Hence, inverse element is itself too.

RBSE Solutions for Class 12 Maths