Rajasthan Board RBSE Class 12 Maths Chapter 10 Definite Integral Ex 10.2
Find the value of the following integrals :
RBSE Solutions For Class 12 Maths Chapter 10.2 Question 1.
![]()
Solution:
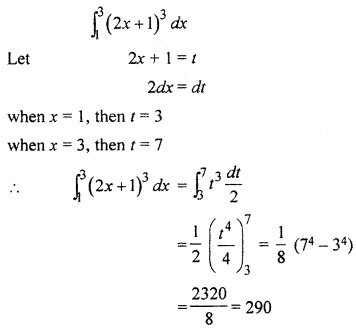
Ex 10.2 Class 12 RBSE Question 2.
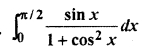
Solution:
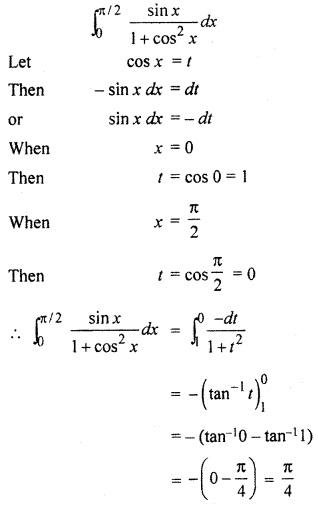
RBSE Solutions For Class 12 Maths Chapter 10 Question 3.
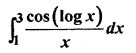
Solution:
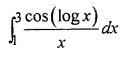
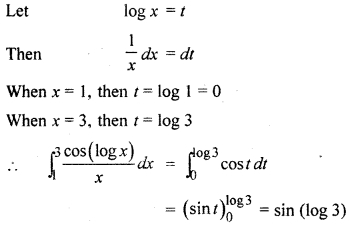
RBSE Solutions For Class 12 Maths Chapter 10 Miscellaneous Question 4.
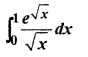
Solution:
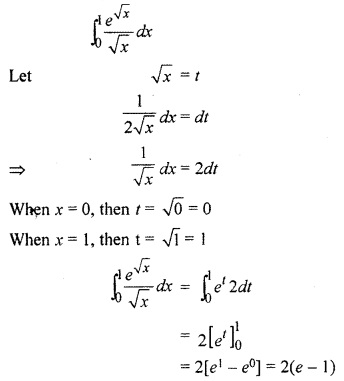
12 Maths RBSE Solution Question 5.
![]()
Solution:
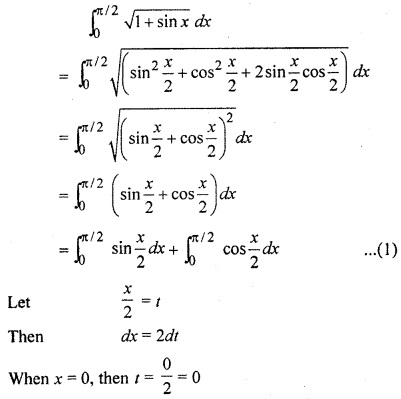
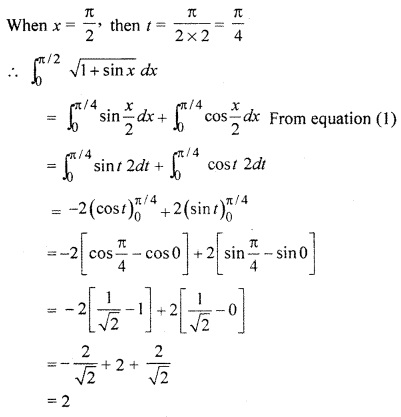
RBSE Solution 12 Math Question 6.
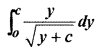
Solution:
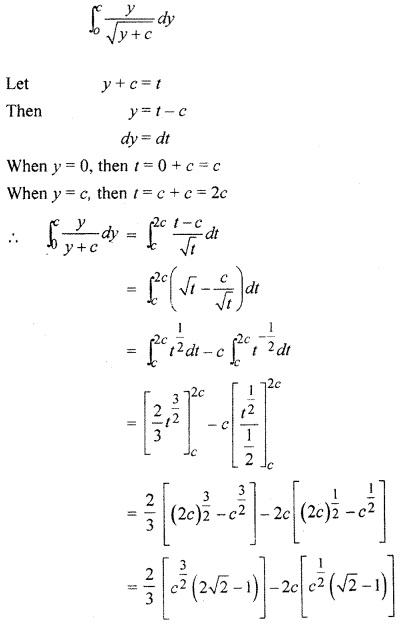
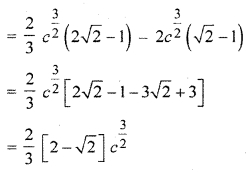
RBSE Solutions Class 12 Maths Ex 10.2 Question 7.
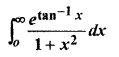
Solution:

Class 12 Math Ex 10.2 Question 8.
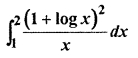
Solution:
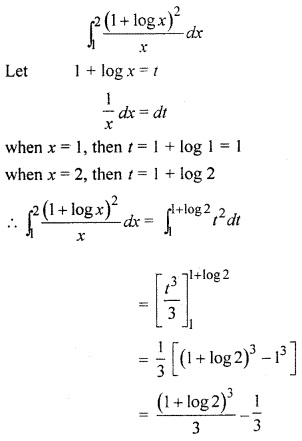
Maths RBSE Solutions Class 12 Question 9.
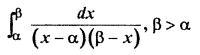
Solution:
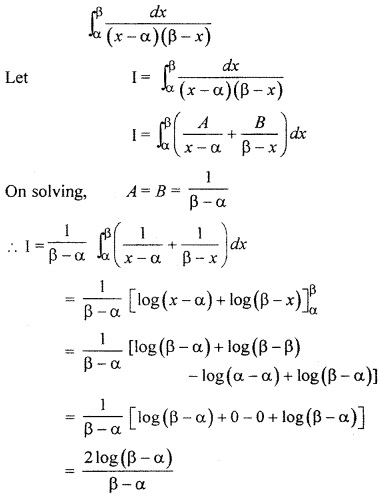
Similar Question
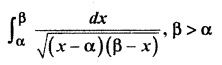
Solution:
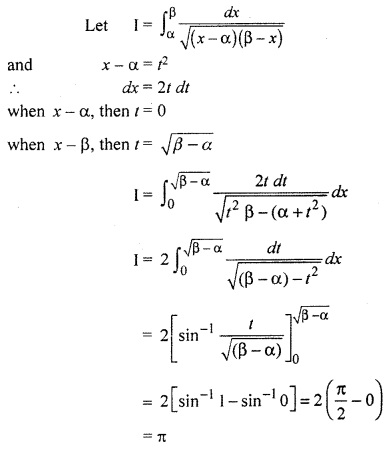
12th RBSE Solutions Question 10.
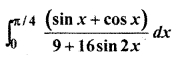
Solution:
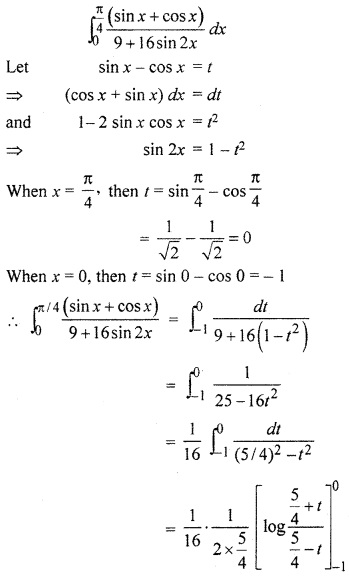
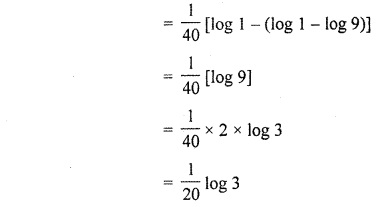
Class 12 Hindi RBSE Solutions Question 11.
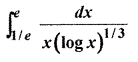
Solution:
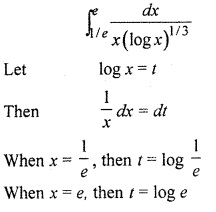
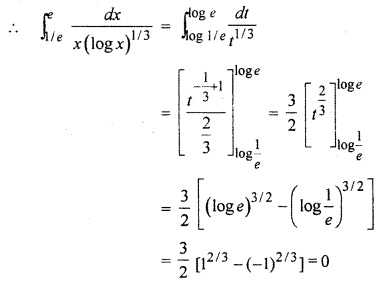
RBSE Solution 12th Class Question 12.
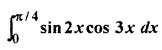
Solution:
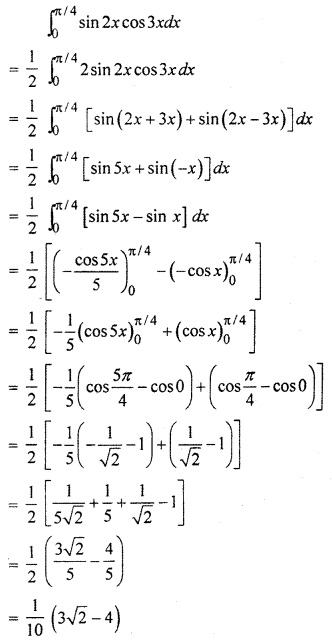
RBSE Solutions Of Class 12 Question 13.
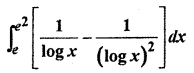
Solution:
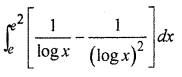
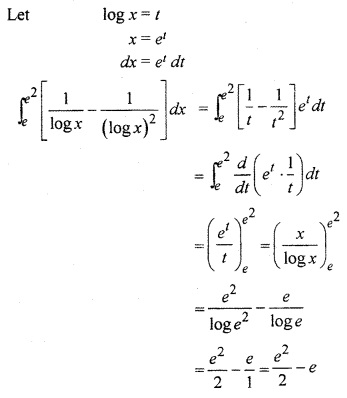
12th Class RBSE Solution Question 14.
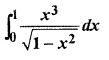
Solution:
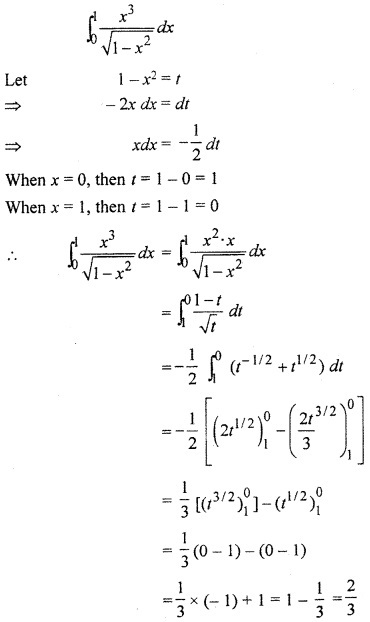
RBSE Solutions For Class 12 Maths Chapter 10.2 Question 15.
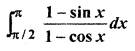
Solution:
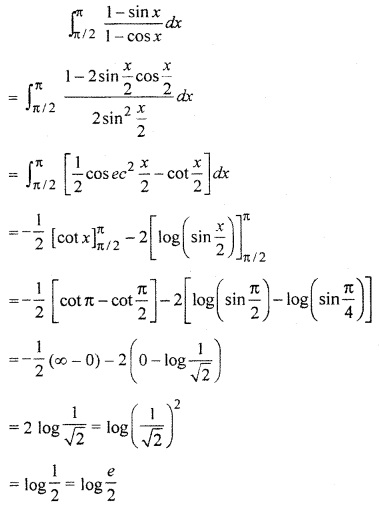
12th RBSE Solution Question 16.
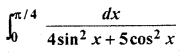
Solution:
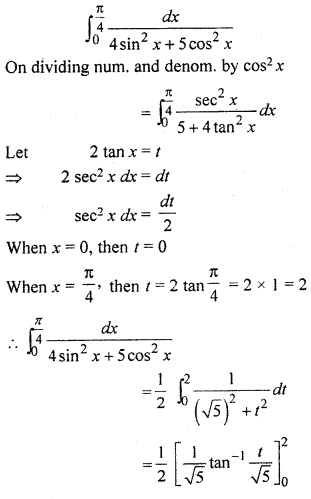
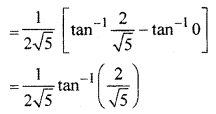
RBSE Solution For Class 12th Question 17.
![]()
Solution:

RBSE Solution Class 12th Maths Question 18.
![]()
Solution:
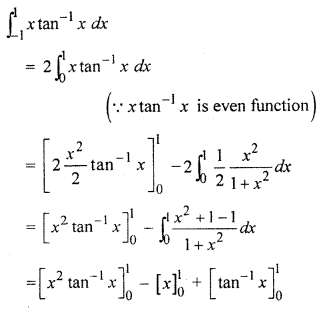
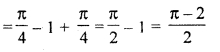
RBSE Solution Class 12 Hindi Question 19.
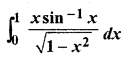
Solution:
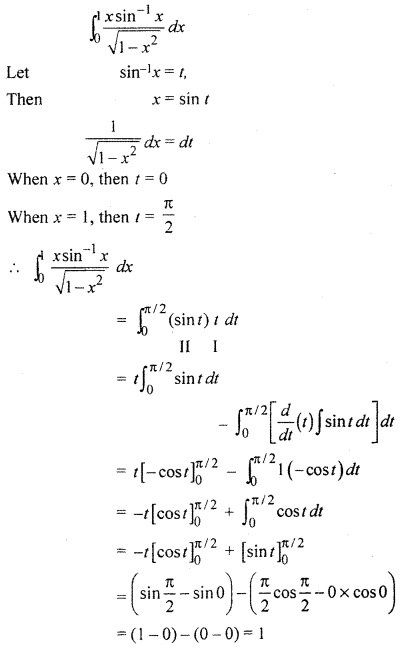
RBSE Solution Of Class 12th Question 20.
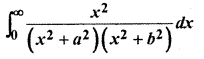
Solution:
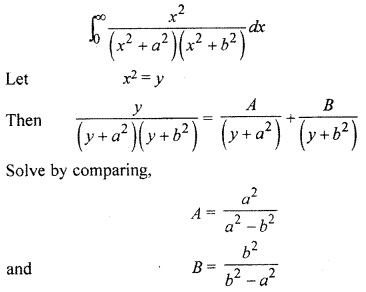

12th Maths RBSE Solution Question 21.
![]()
Solution:
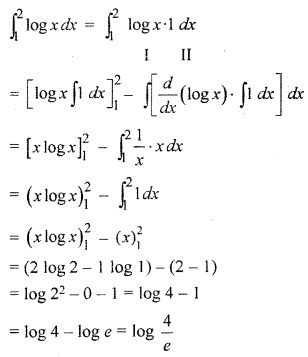
12 Class RBSE Solution Question 22.
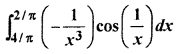
Solution:
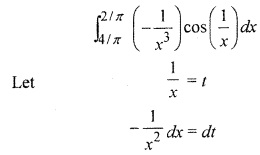
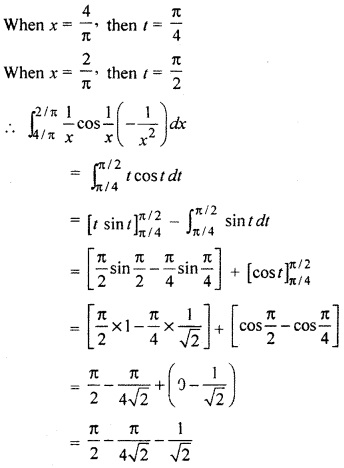
RBSE Solutions 12th Hindi Question 23.
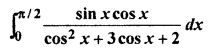
Solution:
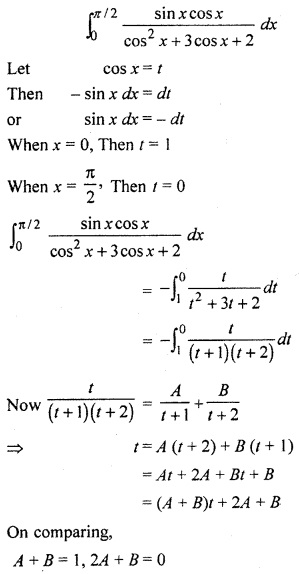
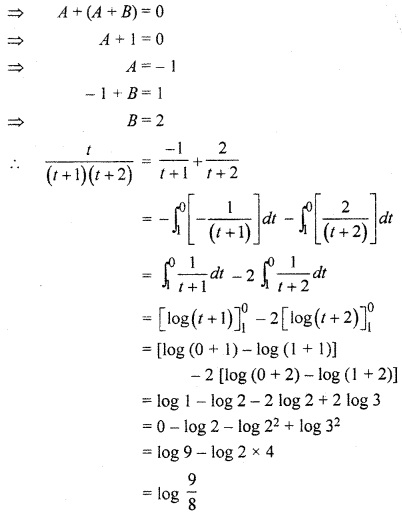
RBSE Solution 12th Question 24.
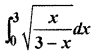
Solution:
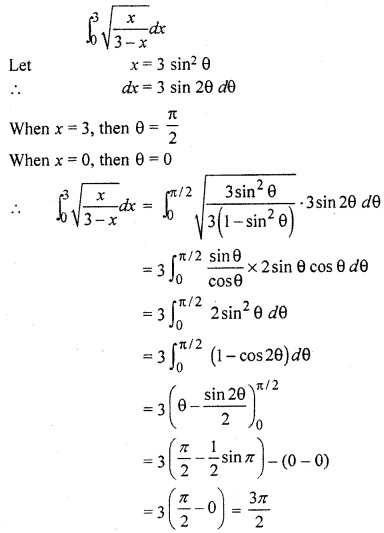
RBSE Solutions 12 Question 25.
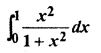
Solution:
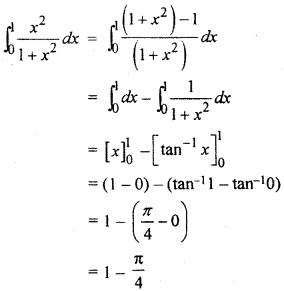
RBSE Solutions 12 Maths Question 26.
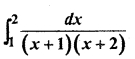
Solution:
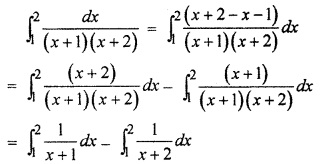
\([\log (x+1)]_{1}^{2}-[\log (x+2)]_{1}^{2}\)
= [log (2 + 1) – log (1 + 1)]
– [log (2+ 2)-log (1 +2)]
= log 3 – log 2 – log 4 + log 3
= 2 log 3 – (log 2 + log 4)
= 2 log 3 – log 8
= log \(\frac { { 3 }^{ 2 } }{ 8 } \) = log \(\frac { 9 }{ 8 } \)