RBSE Solutions for Class 12 Maths Chapter 11 Application of Integral:Quadrature Ex 11.1

Rajasthan Board RBSE Class 12 Maths Chapter 11 Application of Integral:Quadrature Ex 11.1

Question 1.
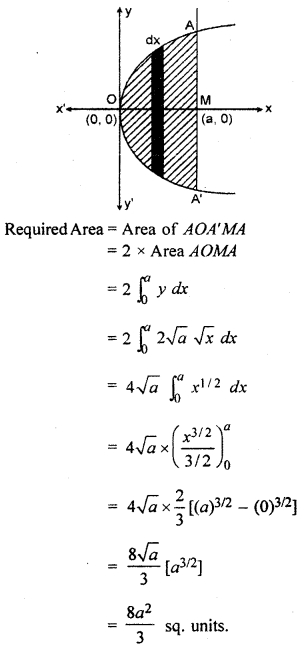
Find the area enclosed by parabola y² = 4ax and its latus rectum.
Solution:
Area bounded by parabola y² = 4ax and its latus rectum is symmetric about x-axis.

Question 2.
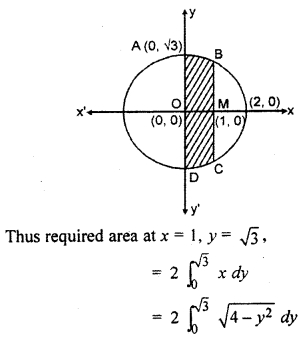
Sketch the circle x² + y² = 4, find area enclosed by y – axis and x = 1.
Solution:
Circle x² + y² = 4, whose centre is (0,0) and radius 2.

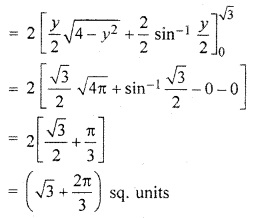
Question 3.
Find the area enclosed by curve y = sin x and x – axis, whereas 0 < x < 2π.
Solution :
The area enclosed by curve y = sin x and x = π and x = 2π has shown in given following figure by shaded part. Table of y = sinx for various volues of x is given below:

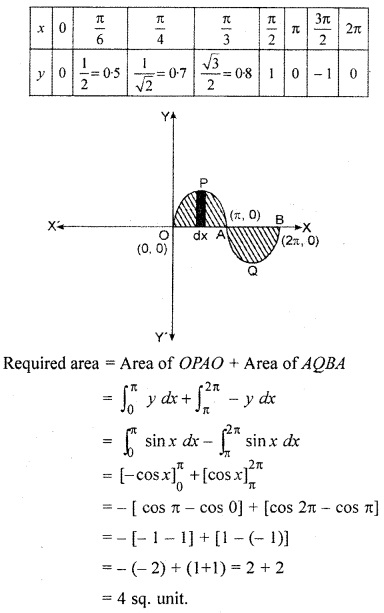
Question 4.
Find the area enclosed by curve y = 2\(\sqrt { x }\) and x = 0, x = 1.
Solution :
y = 2\(\sqrt { x }\) ⇒ y² = 4x, which is a parabola. The area enclosed by curve y² – 4x, x = 0, x = 1 has shown by shaded part in the following figure.

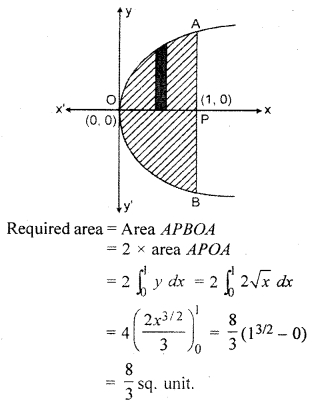
If we take area between only positive coordinates, then we will solve like this
y = 2\(\sqrt { x }\), x = 0, x = 1
Required Area = Area APOA,

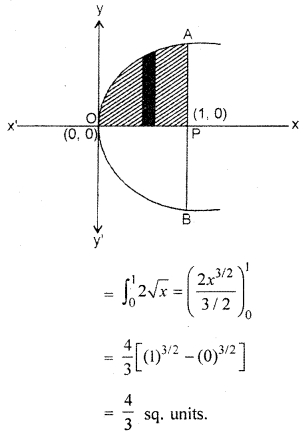
Question 5.
Find the area enclosed by y = | x |, x = – 3, x = 1 and x-axis.
Solution :
y = | x |, x = – 3, x = 1
Thus y = + x and y = -x
Graph of these lines is given below

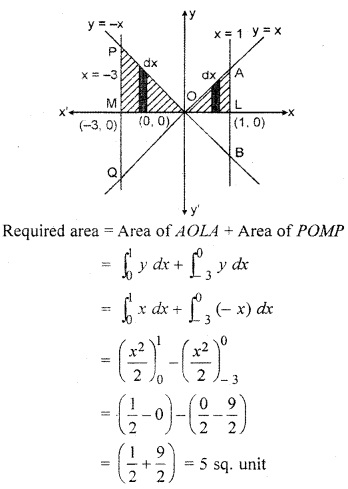
Question 6.
Find the area enclosed by curve x² = 4ay, x-axis and line x = 2.
Solution:
Curve x² = 4ay is a parabola. Its graph is given below.

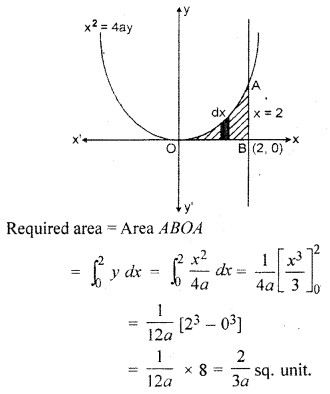
Question 7.
Find the area enclosed by ellipse \(\frac { { x }^{ 2 } }{ 4 } \) + \(\frac { { y }^{ 2 } }{ 9 } \) = 1 and lie above the x – axis
Solution:
The area enclosed by ellipse \(\frac { { x }^{ 2 } }{ 4 } \) + \(\frac { { y }^{ 2 } }{ 9 } \) = 1 and lie above the x axis is shown in the following figure :

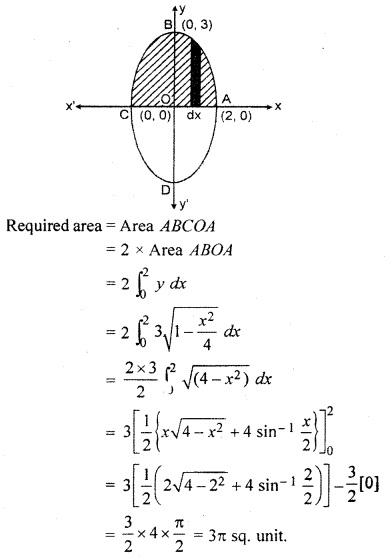
Question 8.
Find the total area of ellipse \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } \) + \(\frac { { y }^{ 2 } }{ { b }^{ 2 } } \) = 1.
Solution:
Total area of ellipse \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } \) + \(\frac { { y }^{ 2 } }{ { b }^{ 2 } } \) = 1 is shown in the following figure.

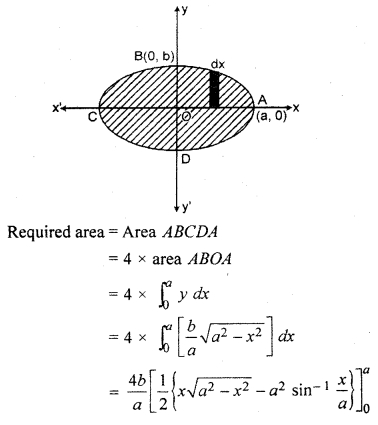
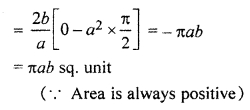
Question 9.
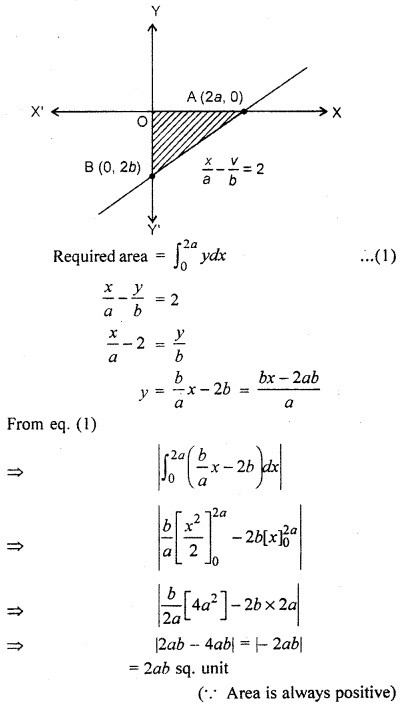
Find the area enclosed by line \(\frac { x }{ a } \) – \(\frac { y }{ b } \) = 2 and co-ordinate axis.
Solution:
Graph of line \(\frac { x }{ a } \) – \(\frac { y }{ b } \) = 2 is as follows:

Question 10.
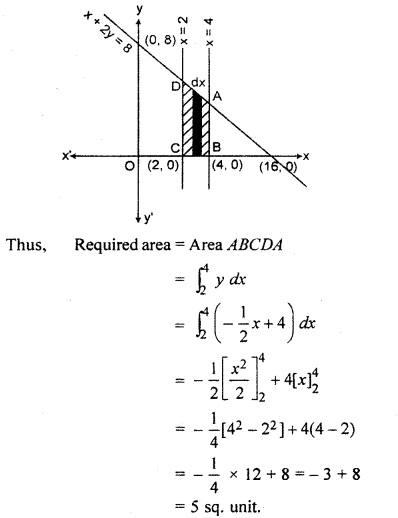
Find the area enclosed by line x + 2y = 8, x = 2, x = 4 and x-axis.
Solution:

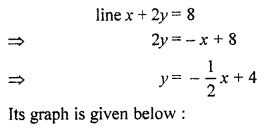
Question 11.
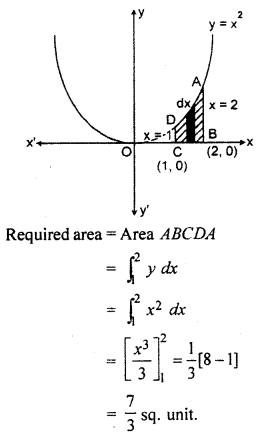
Find the area enclosed by the curve y – x², ordinates x = 1, x = 2 and x-axis.
Solution:
Parabola x² = y is symmetric about x axis. Its vertex is origin (0, 0)
Area enclosed by lines x = 1, x = 2, x-axis and curve x² = y is shown in figure by shaded part.

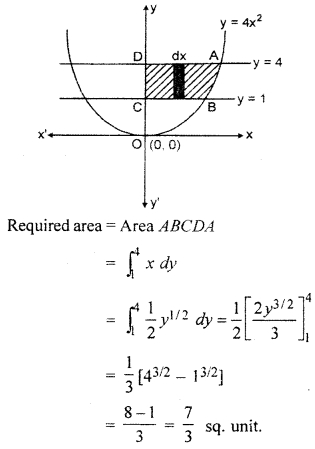
Question 12.
Find the area of the region in the first quadrant enclosed by y = 4x², x = 0, y = 1 and y = 4.
Solution:
∵ y = 4 x²
⇒ x² = \(\frac { 1 }{ 4 } \) y
This is a equation of parabola
Thus x = 0, y = 1, y = 4 area enclosed by and curve y = 4x² is shown in figure by shaded part.

RBSE Solutions for Class 12 Maths