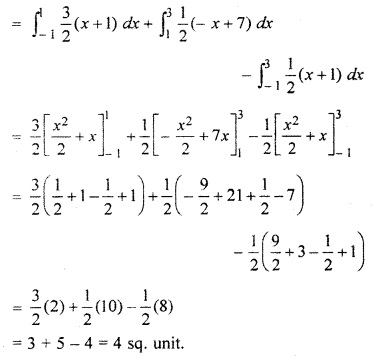RBSE Solutions for Class 12 Maths Chapter 11 Application of Integral:Quadrature Ex 11.2

Rajasthan Board RBSE Class 12 Maths Chapter 11 Application of Integral:Quadrature Ex 11.2

Question 1.
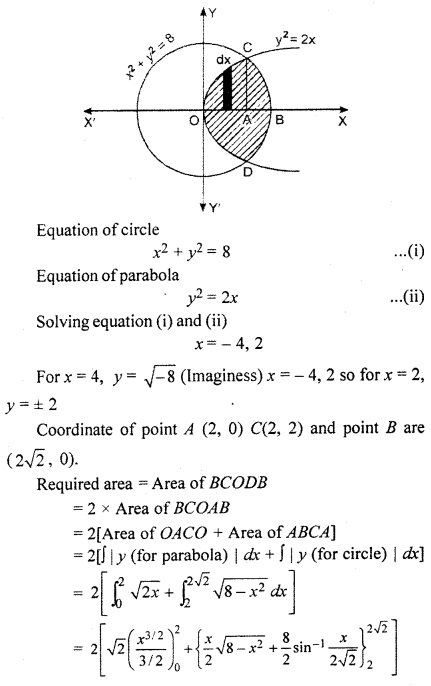
Find the area between the region of parabola. y² = 2x and x² + y² = 8.
Solution:
Required area is shaded in following figure.

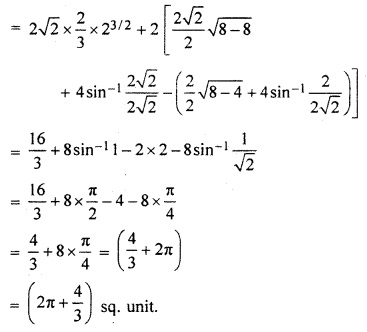
Question 2.
Find the area of the region enclosed by parabola 4y = 3x² and line 3x – 2y + 12 = 0.
Solution:
Parabola 4y = 3x² and line 3x – 2y + 12 = 0 intersect each other at point, A(-2, 3) and B(4, 12). Required area is shaded in the follows figure.

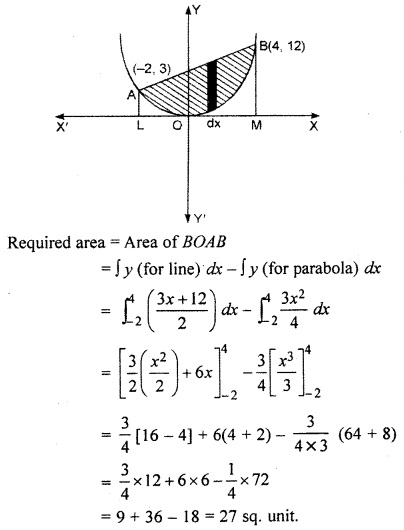
Question 3.
Find the area of the region enclosed by curve y = \(\sqrt { 4-{ x }^{ 2 } } \), x = \(\sqrt { 3 }\) y and x-axis.
Solution:
Curve y = \(\sqrt { 4-{ x }^{ 2 } } \) is circle whose vertex is origin and radius is 2.

Question 4.
Find the area of the region in the first quadrant enclosed by circle x² + y² = 16 and line y = x.
Solution:
Centre of circle x² + y² = 16 is origin and radius is 4 line y = x passes through origin and cuts the circle at A.

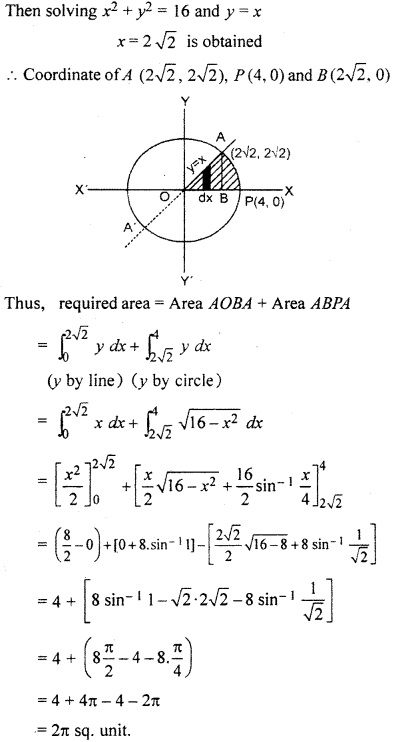
Question 5.
Find the area of common region between parabola y² = 4x and x² = 4y.
Solution:
Equation of given parabolas are
y² = 4x …..(i)
x² = 4y ……(ii)
Solving these, we get (0, 0) and (4, 4) their intersecting points as

Question 6.
Find the area of the region in the first quadrant enclosed by curve x² + y² – 1 and x + y = 1 equation.
Solution:
Given circle x² + y² = 1 its centre passes through origin and radius is 1. x + y = 1 is equation of line which passes through points (1,0) and (0, 1).

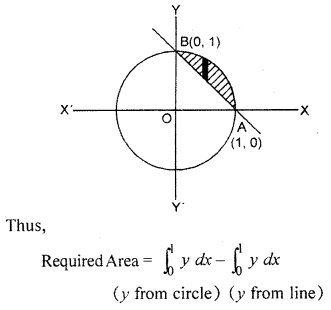
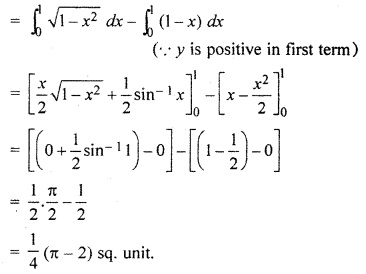
Question 7.
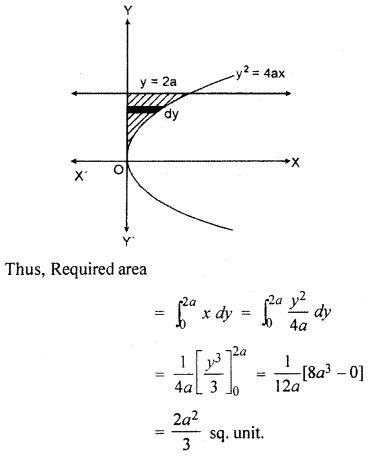
Find the area of the region enclosed by curve y² = 4ax, and line y = 2a and y – axis.
Solution:
Shaded part of following figure shows area enclosed by curve y² = 4ax, line y = 2a and y axis.

Question 8.
Find the area of that portion of circle x² + y² = which lies outside the parabola y² = 6x.
Solution:
Radius of given circle x² + y² = 16 is 4 unit and it passes through origin. Let parabola y² = 6x is interested by circle at points P and Q then solving two equations.
x² + 6x = 16 (∵y² – 6x)
⇒ x² + 6x – 16 = 0
⇒ x + 8x – 2x – 16 = 0
(x + 8) (x – 2) = 0

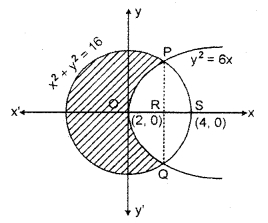
Thus x = – 8, + 2
Here we take positive value of x.
Thus we will take limits 0 and 2, 2 and 4
Area POQSP = 2 × area PORSP
= 2 [area PORP + area PRSP]

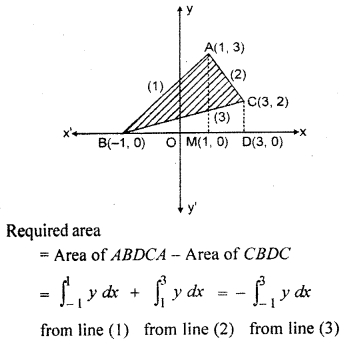
Question 9.
By using integrating method, find the area of ∆ABC whose coordinates of vertices are A(2, 0), 5(4, 5), C(6, 3).
Solution:
In figure, ∆ABC is shaded.

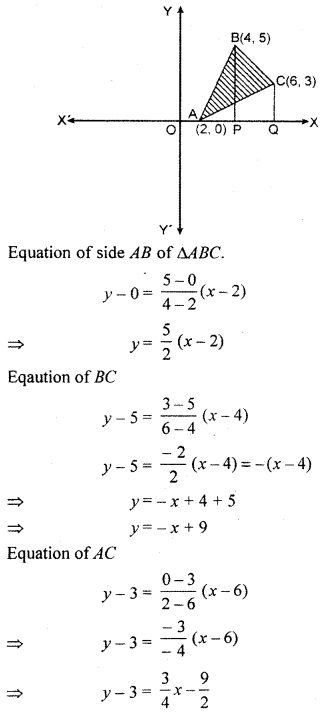
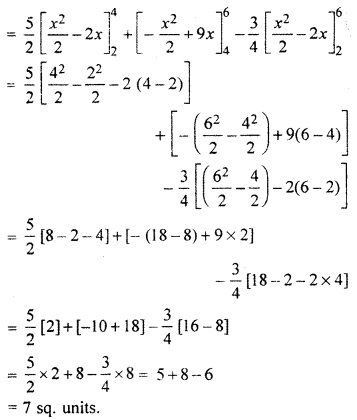
Question 10.
By using intersection method, find the area of triangular prism equations of whose sides are 3x – 2y + 3 = 0, x + 2y – 7 = 0 and x – 2y + 1 = 0. Solution:
Given lines
3x – 27 + 3 = 0 …..(i)
x + 27 – 7 = 0 …..(ii)
and x – 27 + 1 = 0 …..(3)
Solving equation (1) and (2)
x = 1, y = 3
Solving equation (2) and (3)
x = 3, y = 2
Solving equation (3) and (1)
x = -1, y = 0
Now draw the graph of threee lines

RBSE Solutions for Class 12 Maths