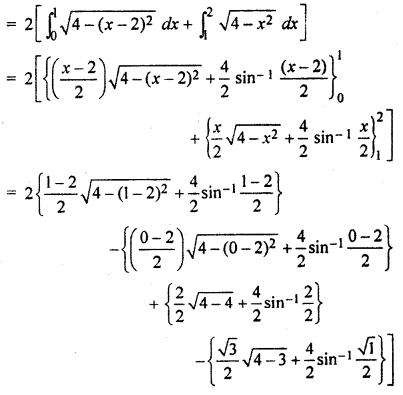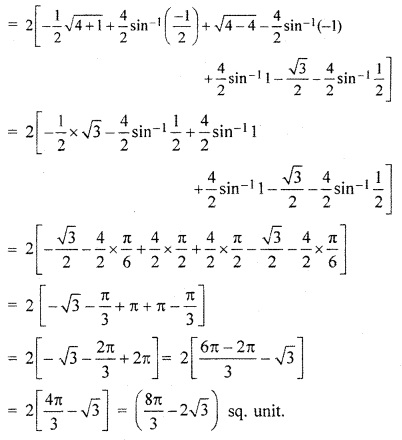Rajasthan Board RBSE Class 12 Maths Chapter 11 Application of Integral:Quadrature Miscellaneous Exercise
Question 1.
Area of the region bounded by the curve y = \(\sqrt { x }\) and y = x is :
(a) 1 sq. unit
(d) \(\frac { 1 }{ 9 } \) sq. unit
(c) \(\frac { 1 }{ 6 } \) sq. unit
(d) \(\frac { 2 }{ 3 } \) sq. unit
Solution:
Curve y = \(\sqrt { x }\) is a parabola whose equation is y2 = x and centre is at origin y = x is a line which passes through origin which is shown in following figure.
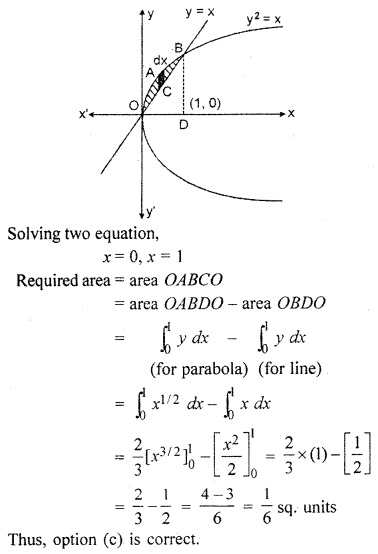
Question 2.
Area of region enclosed by y2 = x and x2 = y is :
(a) \(\frac { 1 }{ 3 } \) sq. unit
(d) 1 sq. unit
(c) \(\frac { 1 }{ 2 } \) sq. unit
(d) 2 sq. unit
Solution:
Sllving given equations
y2 = x …..(i)
x2 = y …..(ii)
We get integration (0,0) and (4,4)
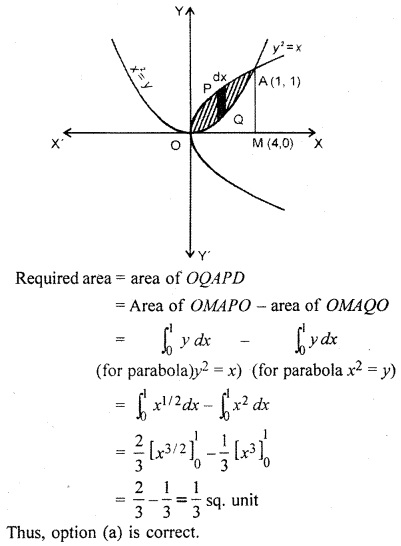
Question 3.
Area of region enclosed by and its latus rectum parabola x2 = 4y is :
(a) \(\frac { 5 }{ 3 } \) sq. unit
(d) \(\frac { 2 }{ 3 } \) sq. unit
(c) \(\frac { 4 }{ 3 } \) sq. unit
(d) \(\frac { 8 }{ 3 } \) sq. unit
Solution:
Graph of parabola x2 = 4y is given below :
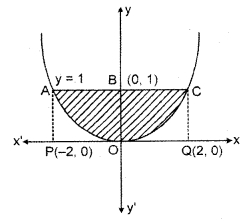
Here, a=1
Thus, latus rectum intersects y axis at (0, 1).
Solving equation of latus rectum y = 1 and equation of parabola x2 = 4y is x = ± 2
Required area = Area AOCBA
= 2[Area OQCBO – Area OQCO)

Question 4.
Area of region enclosed by y = sin x, \(\frac { \pi }{ 2 } \) < x < \(\frac { 3\pi }{ 2 } \) and x-axis is :
(a) 1 sq. unit
(d) 2 sq. unit
(c) \(\frac { 1 }{ 2 } \) sq. unit
(d) 4 sq. unit
Solution:
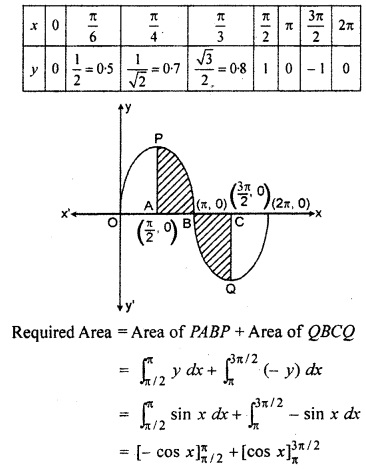
The area enclosed by curve y = sin x and x = π/2 and x = 3rc/2 is shown by shaded part in figure for various values of x, table for values of y = sin x is given below :
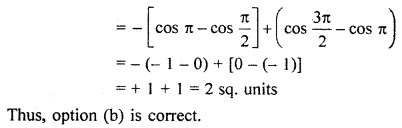
Question 5.
Area of region enclosed by y2 = 2x and circle x2 + y2 = 8 is :
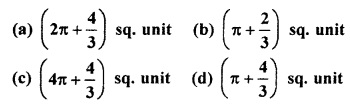
Solution:
y2 = 2x is equation of parabola whose centre (0, 0) and circle whose centre is (0, 0) and radius is 2\(\sqrt { 2 }\) units. Their graph of enclosed area is shown by shaded part.

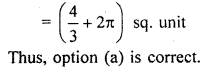
Question 6.
Find the area of the region bounded by parabola y2 = x and line x + y = 2.
Solution:
Area of region bounded by parabola y2 = x and x + y = 2 is shown by shaded part in the following graph.


Question 7.
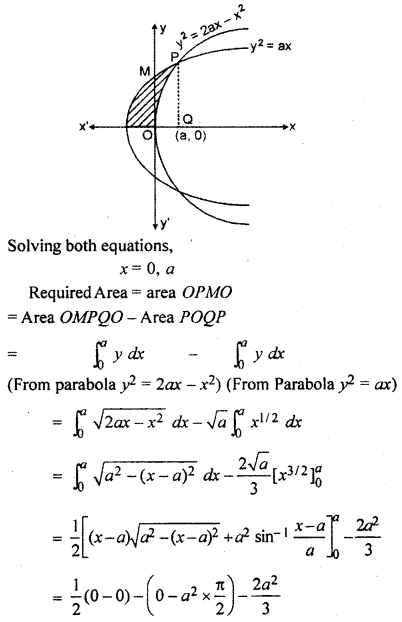
Find the area of the region bounded by curve y2 = 2ax – x2 and y2 = ax
Solution:
Area enclosed by curve y2 = 2ax – x2 and y2 = ax is shown by shaded part in the following graph.
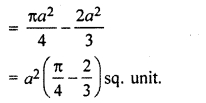
Question 8.
Find the area of region bounded by parabola y = x2 and y = | x |.
Solution:
Curve y = x2 is a parabola whose vertex is (0, 0) and is symmetric about y-axis.
Equation y = | x | represents two lines
When x > 0, then y = x
When x < 0, then y = -x
Intersection points of y = x and parabola y = x2 are O(0, 0) and A (1, 1).
Intersection points of y = – x and parabola y = x2 and O(0, 0) and B (- 1, 1).
The region bounded by lines y = x and y = – x and parabola y = x2 is shown in the following figure.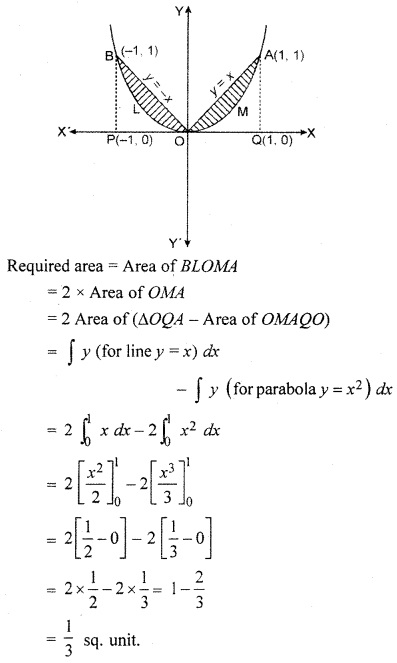
Question 9.
Find the area of the common region bounded by x2 + y2 = 16 and parabola y2 = 6x.
Solution:
Centre of circle x2 + y2 = 16 is origin and radius is 4 unit. Vertex of parabola y2 = 6x is origin. Common part of these curves is shown in figure.
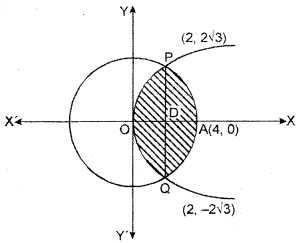
Two curves intersect at point P and Q by solving equations, coordinates of these can be obtained.
Equation of curves x2 + y2 = 16 …..(i)
y2 = 6x …..(ii)

Question 10.
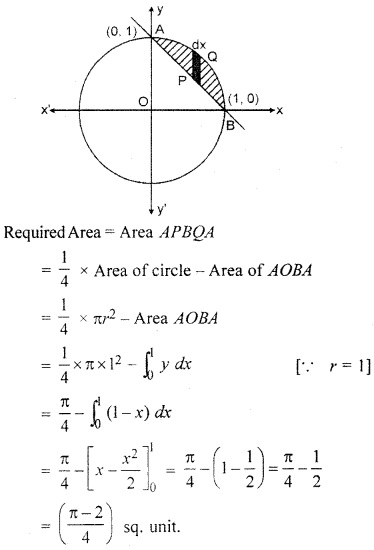
Find the area of the region bounded by curve x2 + y2 = 1 and x + y > 1.
Solution:
Area enclosed by circle x2 + y2 = 1 and line x + y > 1 is shown by shaded part in figure.
Question 11.
By using intersection method, find the area of the triangle whose vertices are (- 1, 0), (1, 2) and (3, 2).
Solution:
Graph of triangle is given below. Required Area is shaded in the figure given below:
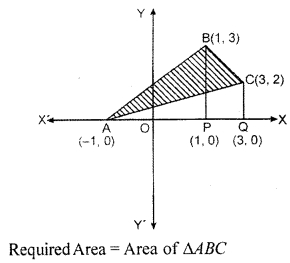
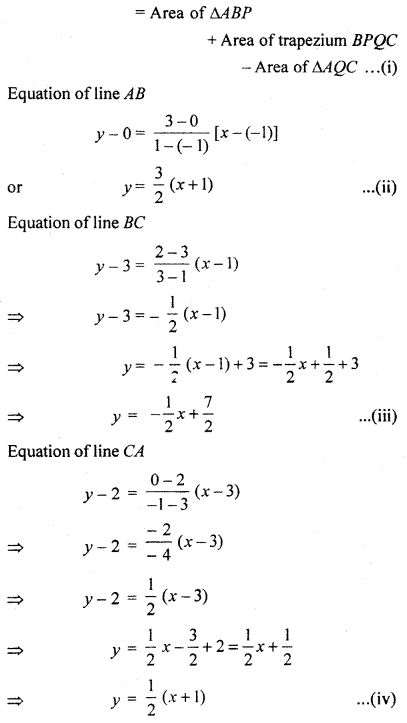

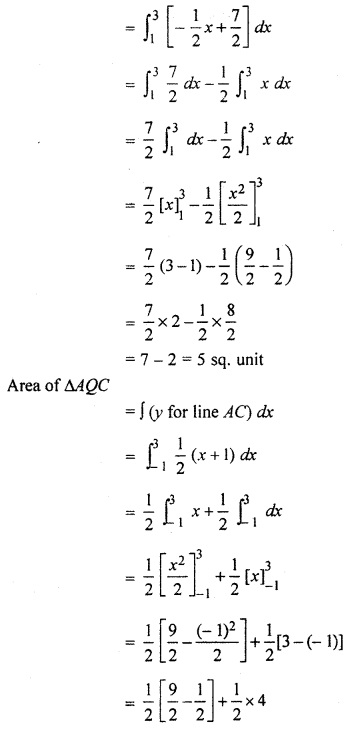
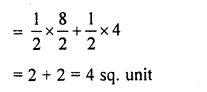
Now, putting values of area ∆ABP, area of trapezium BPAQ and area of ∆AQC in equation (i).
Required Area of ∆ABC
= 3 + 5 – 4 = 4 sq. unit
∴ Area of ∆ABC = 4 sq. unit
Question 12.
Find the area of region bounded by line y = 3 x + 2, x axis and ordinates x = – 1 and x = 1.
Solution:
Area enclosed by line y = 3x + 2, x axis and ordinates x = – 1 and x = 1 is shown below by shaded part.

Question 13.
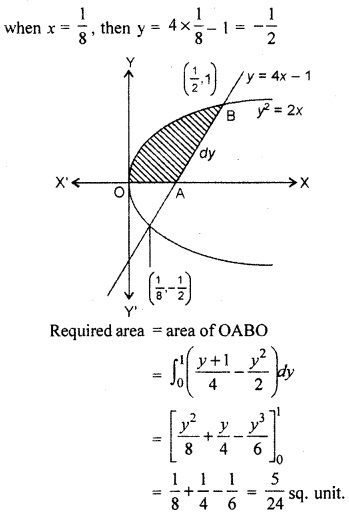
Find the area of the region bounded by y2 = 2x, y = 4x – 1 and y > 0.
Solution:
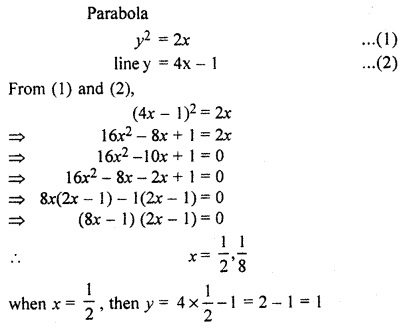
Question 14.
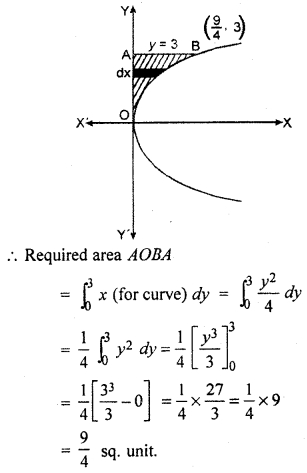
Find the area of the region bounded by curve y2 = 4x, y-axis and line y = 3.
Solution:
Curve y2 = 4x is a parabola whose vertex is origin and symmetric about x-axis. Area enclosed by curved y2 = 4x and line y = 3 is shown by shaded part in figure given below.
Question 15.
Find the area of the region bounded by two circles x2 + y2 = 4 and (x – 2)2 + y2 = 4.
Solution:
Equations of given circles
x2 + y2 = 4 ….(i)
and (x – 2)2 + y2 = 4 ….(ii)
Centre of circle from equation –
(i) is at origin (0, 0) and radius is 2 unit. Centre of circle of equation
(ii) is (2, 0) and at x axis and radius is 2 unit. Required enclosed area is shown by shaded part in figure.
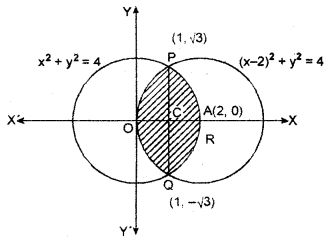
Solving equation (i) and (ii)
Obtained intersecting points of circles are p(1,\(\sqrt { 3 }\)) and Q (1 – \(\sqrt { 3 }\))
Out of two circles one symmetric about x axis
∴ Required area
= 2(Area OPACO) = 2 [Area OPCO + Area CPAC]
= 2[Area OPCO (part of circle (x – 2)2 + y2 = 4)
+ Area CPAC (part of circle x2 + y2 = 4)
∴ Required Area
= 2 ∫ y dx (for circle (x – 2)2 + y2 = 4)
+ ∫ y dx (for circle x2 + y2 = 4)