Rajasthan Board RBSE Class 12 Maths Chapter 12 Differential Equation Miscellaneous Exercise
Question 1.
Solution of differential equation
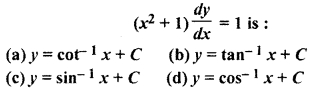
Solution:

Hence, option (b) is correct.
Question 2.
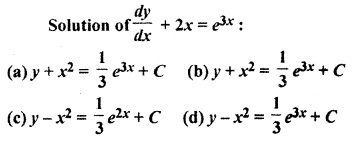
Solution:
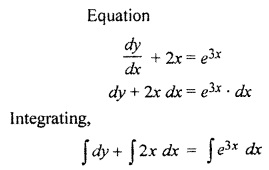
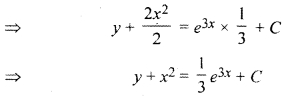
Thus Option (a) is correct.
Question 3.
Solution of \(\frac { dy }{ dx } \) + cos x tan y = 0 is :
(a) log sin y + sin x + C
(b) log sin x sin y = C
(c) sin y + log sin x + C
(d) sin x sin y + C
Solution:
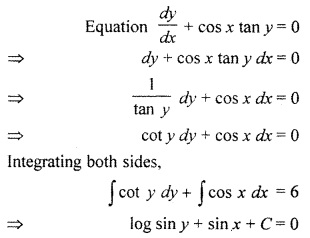
Hence, option (a) is correct.
Question 4.
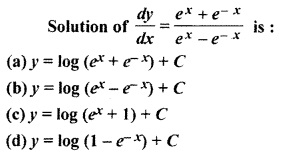
Solution:
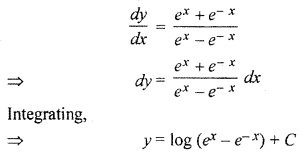
Thus Option (b) is correct.
Question 5.
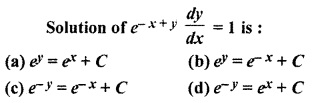
Solution:
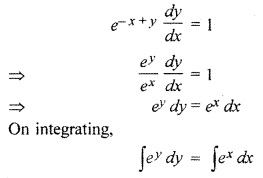
![]()
Thus Option (a) is correct.
Question 6.
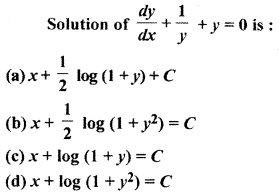
Solution:
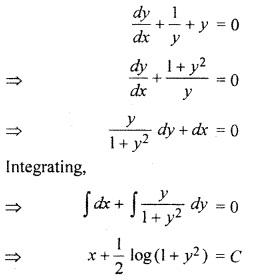
Thus Option (b) is correct.
Question 7.
Solution \(\frac { dy }{ dx } \) = cos2 y is :
(a) x + tan y = C
(b) tan y = x + C
(c) sin y + x = C
(d) sin y – x = C
Solution:
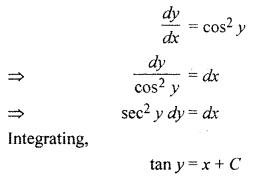
Thus Option (b) is correct.
Question 8.
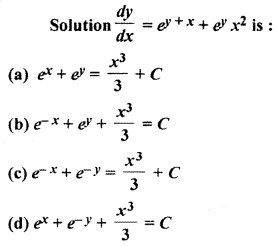
Solution:
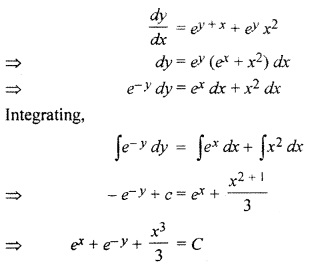
Thus Option (d) is correct.
Question 9.
By which displacement the differenting equation
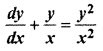
will be correct into linear equation :
(a) y = 1
(b) y2 = t
(c) \(\frac { 1 }{ y } \) = t
(d) \(\frac { 1 }{ { y }^{ 2 } } \) = t
Solution:
Hence, option (c) is correct.
Question 10.
By which displacement the differential equation
![]()
will be correct into linear equation :
(a) \(\frac { 1 }{ y } \) = v
(b) y-2 = v
(c) y-3 = v
(d) y3 = v
Solution:
Hence, option (b) is correct.
Question 11.
Find the general solution of differential equation
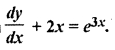
Solution:
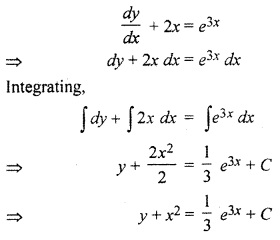
This is required solution
Question 12.
Find the integrating factor of differential equation \(\frac { dy }{ dx } \) + y tan x = sin x.
Solution:
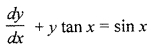
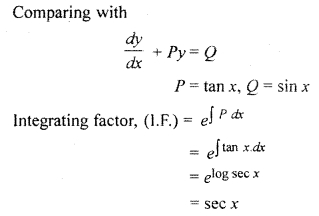
Question 13.
Find the integrating factor of differential equation
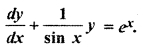
Solution:

Question 14.
Write the form of differential equation dy cos (x + y) \(\frac { dx }{ dx } \) = 1.
Solution:
Given equation is of the form of converting variables separately.
Question 15.
Write the form of differential function
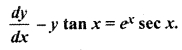
Solution:
Linear equation
Question 16.
Write the general solution of the following differential equation
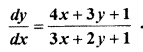
Solution:
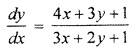



Similar Question
If we take equation
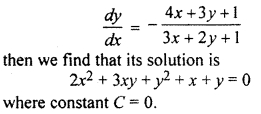
Question 17.
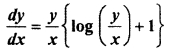
Solution:

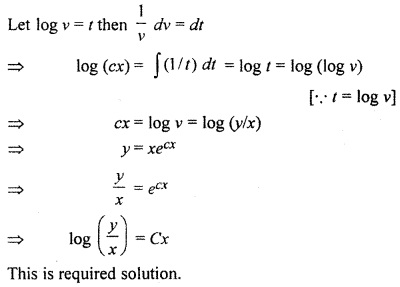
Question 18.
![]()
Solution:

Question 19.
![]()
Solution:
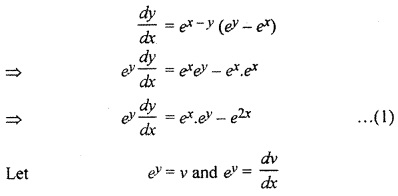

Question 20.
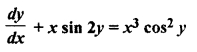
Solution:
