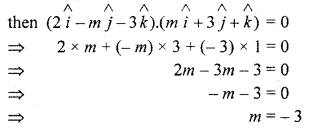RBSE Solutions for Class 12 Maths Chapter 14 Three Dimensional Geometry Ex 14.7

Rajasthan Board RBSE Class 12 Maths Chapter 14 Three Dimensional Geometry Ex 14.7

Question 1.
Find the angle between the planes :

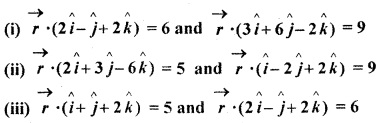
Solution:

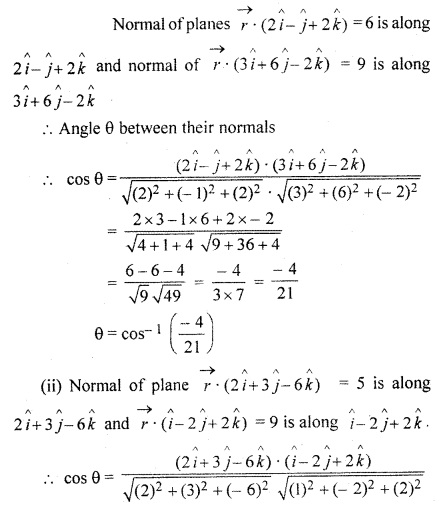
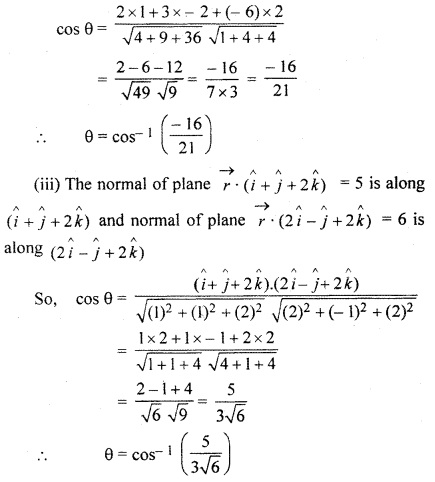
Question 2.
Find the angle between the planes :
(i) x + y + 2z = 9 and 2x – y + z = 15
(ii) 2 x – y + z = 4 and x + y + 2z = 3
(iii) x + y – 2z = 3 and 2x – 2y + z = 5
Solution:
If plane are a₁x + b₁y + c₁z + d₁ = 0 and a₂x + b₂y + c₂z + d₂ = 0 then angle between them is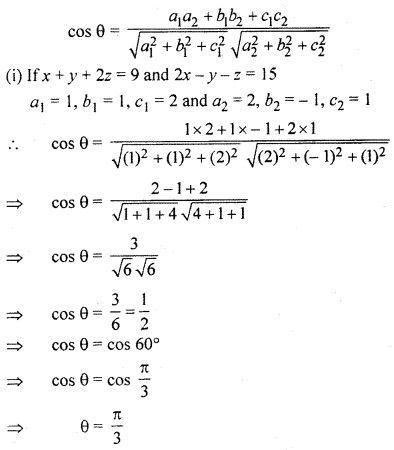

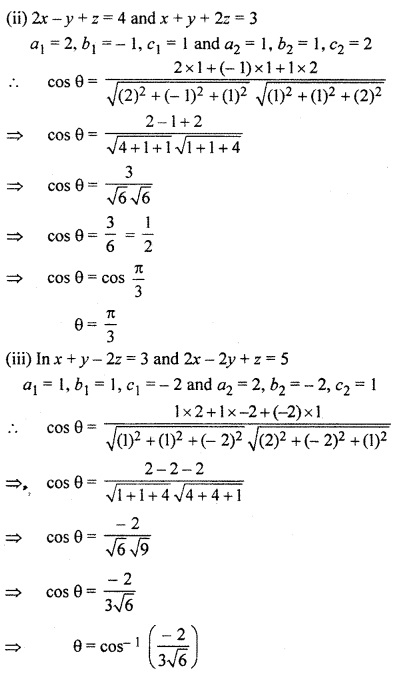
Question 3.
Show that following planes are at right angles :

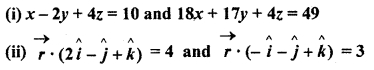
Solution:
x – 2y + 4z = 10 and 18x + 17y + 4z = 49
a₁ = 1,b₁ = -2, c₁ = 4 and a₂ = 18 b₂ = 17, c₂ = 4

(i) Planes will be perpendicular if
a₁ a₂ + b₁b₂ + c₁c₂ = 0
L.H.S. = 1 × 18 + (-2) × 17 + 4 × 4
= 18 – 34+16
= – 34 + 34
= 0
∴ L.H.S. = R.H.S.

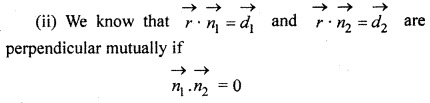
Question 4.
Find λ, if following planes are perpendicular to each other:

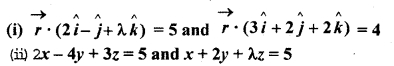
Solution:

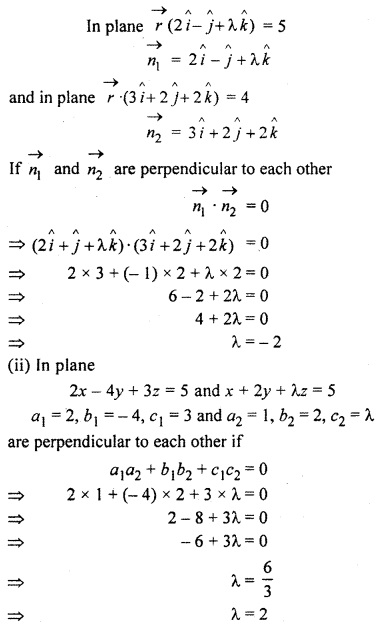
Question 5.
Find the angle between the line \(\frac { x+1 }{ 3 } \) = \(\frac { y-1 }{ 2 } \) = \(\frac { z-2 }{ 4 } \) and the plane 2x + y – 3z + 4 = 0
Solution:
Normal vector of the plane 2x + y – 3z + 4 = 0

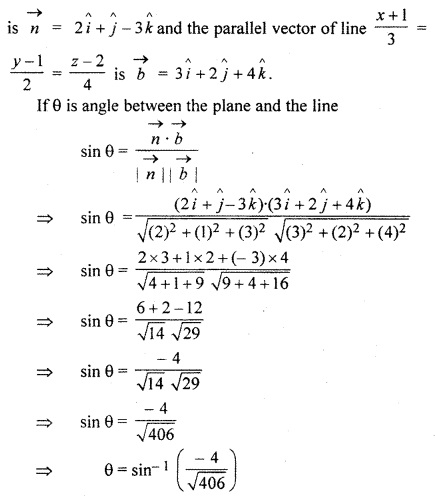
Question 6.
Find the ngle between the line \(\frac { x-2 }{ 3 } \) = \(\frac { y+1 }{ -1 } \) = \(\frac { z-3 }{ 2 } \) and the plane 3x + 4y + z + 5 = 0.
Solution:

Question 7.
Find the angle between

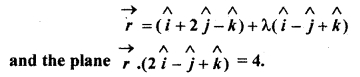
Solution:
We know that the angle between the line and the plane is

Question 8.
Find the angle between

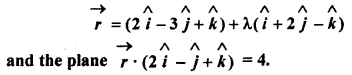
Solution:
We know that angle between the line

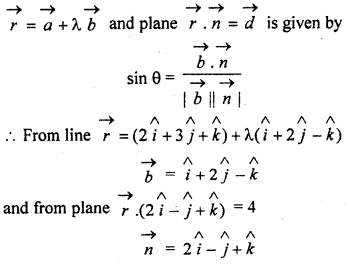
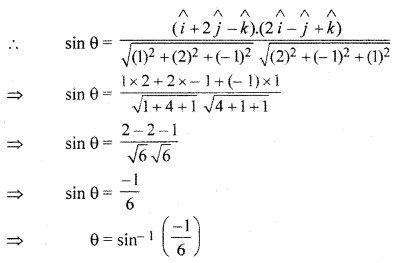
Question 9.
Determine the value of m, if line

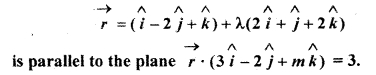
Solution:

Question 10.
Find m, if line

is parallel to the plane

Solution:
If given line is parallel to given plane

RBSE Solutions for Class 12 Maths